TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.2 Snavel- en zandloperfiguren VWO 3
Boek: Getal & Ruimte - Gelijkvormigheid VWO 3 (deel 1) opgaven 19 t/m 35, 2011Met behulp van snavelfiguren en zandloperfiguren kunnen we zijden uitrekenen bij gelijkvormige driehoeken.
Zoek naar evenwijdige lijnen om de juiste driehoeken te vinden voor gelijkvormigheid.
Bij snavelfiguren kunnen we F-hoeken vinden en bij zandloperfiguren kunnen we Z-hoeken onderscheiden.
Op deze wijze maken we weer gebruik van een verhoudingstabel en berekenen zo de onbekende zijde(n).
Zoek naar evenwijdige lijnen om de juiste driehoeken te vinden voor gelijkvormigheid.
Bij snavelfiguren kunnen we F-hoeken vinden en bij zandloperfiguren kunnen we Z-hoeken onderscheiden.
Op deze wijze maken we weer gebruik van een verhoudingstabel en berekenen zo de onbekende zijde(n).
19.
Driehoek BEF ∼ driehoek AED en driehoek BEF ∼ driehoek CDF
20.
b.
AQ = (12 x 3) / 9 = 4
21.
b.
CQ = (2 x 4) / 3 = 8 / 3 ≈ 2,7
22.
a.
=>
PC = (8 x 3) / 7 = 24 / 7 ≈ 3,43
b.
Omdat ∠B recht is, geldt:
AB2 + BQ2 = AQ2
AQ2 = 113
AQ = √113
Bereken nu PQ met de Stelling van Pythagoras:
PC2 + CQ2 = PQ2
(3,43)2 + 32 = PQ2
PQ2 = 20,755
PQ = 4,56
AP = AQ - PQ
AP = √113 - 4,56
AP ≈ 6,07
23.
=>
BF = (1,5 x 3) / 2 = 2,25
24.
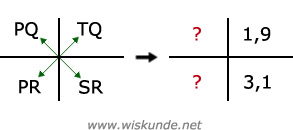
Om PQ te bepalen, moet je ook PR weten.
25.
=>
x ⋅ 6 = (x + 8,4) ⋅ 1,8
6x = 1,8x + 15,12 (links en rechts delen door 6)
x = 0,3x + 2,52
0,7x = 2,52
x = 3,6
Dus CE = 3,6
b. EF met Stelling van Pythagoras:
CE2 + CF2 = EF2
3,62 + 1,82 = EF2
EF2 = 16,2
EF = √16,2
EF ≈ 4,0
26.
=>
x ⋅ 6,2 = 2,6 ⋅ (6,6 - x)
6,2x = 17,16 - 2,6x
8,8x = 17,16
x = 1,95
AC = 6,6 - x = 6,6 - 1,95 = 4,65
b. AB met Stelling van Pythagoras:
AB2 + AC2 = BC2
AB2 + 4,652 = 6,22
AB2 = 16,8175
AB = √16,8175
AB ≈ 4,1
Oppervlakte(ABC) = 1/2 x basis x hoogte
Oppervlakte(ABC) = 1/2 x AB x AC = 1/2 x 4,1 x 4,65 = 9,5325
Oppervlakte(ABC) ≈ 9,5
27.
Driehoek ABC ∼ driehoek MNC
=>
x = (5 x 9) / 4 = 11,25
Dus BC = 11,25
MN = (8 x 5) / 11,15 ≈ 3,6
Wat is de vergrotingsfactor bij driehoek KLC en driehoek MNC? Beeld : origineel = KC : MC = 6 / 4 = 1,5
1,5 x MC = CK
Dus: MN x 1,5 = KL
KL = 1,5 x 3,6 = 5,4
b.
Driehoek KCL ∼ driehoek MCN
=>
4 ⋅ (x + 5) = 6 ⋅ 5
4x + 20 = 30
4x = 10
x = 2,5
Dus LN = 2,5
Bij a. hebben we gezien dat BC = 11,25.
BC = BL + LN + CN
11,25 = BL + 2,5 + 5
BL = 3,75
28.
2(x + 6) = 9x
2x + 12 = 9x
-7x = -12
x = 12/7
x ≈ 1,7 meter
b.
2,5(y + 3,5) = 3,5 x 9
2,5y + 8,75 = 31,5
2,5y = 22,75
y = 9,1
Driehoek BEF ∼ driehoek AED en driehoek BEF ∼ driehoek CDF
20.
Tip:
Omdat er sprake is van een parallellogram geldt dat DC evenwijdig is aan AB.
Op basis van evenwijdigheid kunnen we een snavel- en/of een zandloperfiguur ontdekken.
a.Omdat er sprake is van een parallellogram geldt dat DC evenwijdig is aan AB.
Op basis van evenwijdigheid kunnen we een snavel- en/of een zandloperfiguur ontdekken.
| AQ | AP |
| DC | DP |
| AQ | 3 |
| 12 | 9 |
AQ = (12 x 3) / 9 = 4
21.
Tip:
PC = AB - DP = 5 - 3 = 2
a.PC = AB - DP = 5 - 3 = 2
| CQ | PC | PQ |
| AD | DP | AP |
| CQ | 2 |
| 4 | 3 |
CQ = (2 x 4) / 3 = 8 / 3 ≈ 2,7
22.
Tip:
Omdat ABCD een rechthoek is, weten we zeker dat PC evenwijdig is met AB. Hierdoor is er sprake van een snavelfiguur.
Ook is er sprake van een zandloperfiguur. Probeer beide en kijk welke lukt.
De snavelbek lukt:Omdat ABCD een rechthoek is, weten we zeker dat PC evenwijdig is met AB. Hierdoor is er sprake van een snavelfiguur.
Ook is er sprake van een zandloperfiguur. Probeer beide en kijk welke lukt.
a.
| PC | CQ | PQ |
| AB | BQ | AQ |
| PC | 3 | PQ |
| 8 | 7 | AQ |
PC = (8 x 3) / 7 = 24 / 7 ≈ 3,43
b.
Omdat ∠B recht is, geldt:
AB2 + BQ2 = AQ2
AQ2 = 113
AQ = √113
Bereken nu PQ met de Stelling van Pythagoras:
PC2 + CQ2 = PQ2
(3,43)2 + 32 = PQ2
PQ2 = 20,755
PQ = 4,56
AP = AQ - PQ
AP = √113 - 4,56
AP ≈ 6,07
23.
Tip:
Omdat ABCD een parallellogram is, geldt dat DE is evenwijdig met BC. Hieruit volgt ook dat AE evenwijdig is met BC. Dus we hebben een zandloper gevonden.
Tevens: BC = AD = 3
Omdat ABCD een parallellogram is, geldt dat DE is evenwijdig met BC. Hieruit volgt ook dat AE evenwijdig is met BC. Dus we hebben een zandloper gevonden.
Tevens: BC = AD = 3
| AE | AF | EF |
| BC | BF | CF |
| 2 | 1,5 | EF |
| 3 | BF | CF |
BF = (1,5 x 3) / 2 = 2,25
24.
Tip:
Om een kruisproduct op te lossen, mag je maar 1 onbekende hebben.
PQ = ( PR x TQ ) / SR = ( PR x 1,9 ) / 3,1Om een kruisproduct op te lossen, mag je maar 1 onbekende hebben.
Om PQ te bepalen, moet je ook PR weten.

25.
Tip:
Draai je boek om. Dan zie je de driehoeken voor de snavelbek beter.
Stel EC = x dan DE = (x + 8,4).
Als je EC weet, dan bereken je EF met Pythagoras.
a. Driehoek ECF ∼ driehoek EDADraai je boek om. Dan zie je de driehoeken voor de snavelbek beter.
Stel EC = x dan DE = (x + 8,4).
Als je EC weet, dan bereken je EF met Pythagoras.
| CE | CF | EF |
| DE | AD | AE |
=>
| x | 1,8 | EF |
| (x + 8,4) | 6 | AE |
x ⋅ 6 = (x + 8,4) ⋅ 1,8
6x = 1,8x + 15,12 (links en rechts delen door 6)
x = 0,3x + 2,52
0,7x = 2,52
x = 3,6
Dus CE = 3,6
b. EF met Stelling van Pythagoras:
CE2 + CF2 = EF2
3,62 + 1,82 = EF2
EF2 = 16,2
EF = √16,2
EF ≈ 4,0
26.
Tip:
Stel CD = x dan AC = (6,6 - x)
oppervlakte driehoek = 1/2 x basis x hoogte
a. Driehoek CDE ∼ driehoek CABStel CD = x dan AC = (6,6 - x)
oppervlakte driehoek = 1/2 x basis x hoogte
| driehoek CDE | CD | DE | CE |
| driehoek CAB | AC | AB | BC |
=>
| x | DE | 2,6 |
| (6,6 - x) | AB | 6,2 |
x ⋅ 6,2 = 2,6 ⋅ (6,6 - x)
6,2x = 17,16 - 2,6x
8,8x = 17,16
x = 1,95
AC = 6,6 - x = 6,6 - 1,95 = 4,65
b. AB met Stelling van Pythagoras:
AB2 + AC2 = BC2
AB2 + 4,652 = 6,22
AB2 = 16,8175
AB = √16,8175
AB ≈ 4,1
Oppervlakte(ABC) = 1/2 x basis x hoogte
Oppervlakte(ABC) = 1/2 x AB x AC = 1/2 x 4,1 x 4,65 = 9,5325
Oppervlakte(ABC) ≈ 9,5
27.
Tip:
Bij b. Stel LN = x dan LC = (x + 5)
a.Bij b. Stel LN = x dan LC = (x + 5)
Driehoek ABC ∼ driehoek MNC
| driehoek ABC | AB | BC | AC |
| driehoek MNC | MN | NC | MC |
=>
| 8 | x | 9 |
| MN | 5 | 4 |
x = (5 x 9) / 4 = 11,25
Dus BC = 11,25
MN = (8 x 5) / 11,15 ≈ 3,6
Wat is de vergrotingsfactor bij driehoek KLC en driehoek MNC? Beeld : origineel = KC : MC = 6 / 4 = 1,5
1,5 x MC = CK
Dus: MN x 1,5 = KL
KL = 1,5 x 3,6 = 5,4
b.
Driehoek KCL ∼ driehoek MCN
| driehoek KCL | KC | CL | KL |
| driehoek MCN | MC | CN | MN |
=>
| 6 | (x + 5) | 5,4 |
| 4 | 5 | 3,6 |
4 ⋅ (x + 5) = 6 ⋅ 5
4x + 20 = 30
4x = 10
x = 2,5
Dus LN = 2,5
Bij a. hebben we gezien dat BC = 11,25.
BC = BL + LN + CN
11,25 = BL + 2,5 + 5
BL = 3,75
28.
Tip:
Werk het kruisproduct uit.
a.Werk het kruisproduct uit.
2(x + 6) = 9x
2x + 12 = 9x
-7x = -12
x = 12/7
x ≈ 1,7 meter
b.
| 3,5 | 2,5 |
| y + 3,5 | 9 |
2,5(y + 3,5) = 3,5 x 9
2,5y + 8,75 = 31,5
2,5y = 22,75
y = 9,1
29.
=>
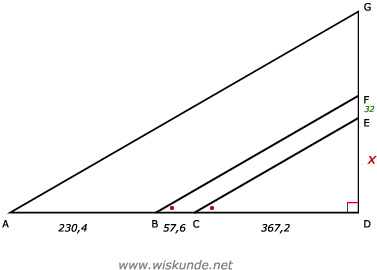
x ⋅ 424,8 = 367,2 ⋅ (x + 32)
424,8x = 367,2x + 11750,4
57,6x = 11750,4
x = 204
Dus DE = 204
Driehoek ADG ∼ driehoek CDE
=>
DG = (655,2 x 204) / 367,2 = 364
Dus hoogte van de toren is 364 meter.
30.
DE2 = 52 + 122
DE2 = 169
DE = √169 = 13
Driehoek ASD ∼ driehoek CSE (i.v.m. zandloperfiguur)
=>
7 ⋅ (13 - x) = 5 ⋅ x
91 - 7x = 5x
-12x = -91
12x = 91
x = 91/12
x ≈ 7,58
x ≈ 7,6
Dus DS = 7,6
31.
BD2 + 152 = 252
BD2 = 400
BD = √400 = 20
Driehoek ABS ∼ driehoek CDS (i.v.m. zandloperfiguur)
=>
We krijgen het volgende kruisproduct:
25(20 - x) = 10x
500 - 25x = 10x
-35x = -500
x = -500 / -35
x ≈ 14,3
Dus: BS = 20 - x = 20 - 14,3 = 5,7
32.
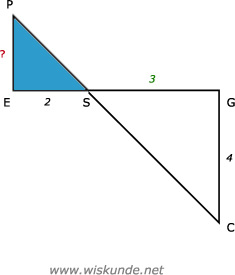
32 + 42 = GE2
GE2 = 25
GE = √25 = 5
GS = GE - ES = 5 - 2 = 3
Driehoek ESP ∼ driehoek GSC (i.v.m. zandloperfiguur)
=>
We krijgen het volgende kruisproduct:
EP = (2 x 4) / 3 = 8/3 = 2 2/3
33.
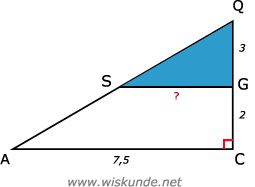
62 + 4,52 = AC2
AC2 = 56,25
AC = √56,25
AC = 7,5
Dus EG = AC = 7,5
Driehoek ACQ ∼ driehoek SGQ (i.v.m. snavelfiguur)
=>
We krijgen het volgende kruisproduct:
SG = (7,5 x 3) / 5 = 4,5
Dus: ES = EG - SG = 7,5 - 4,5 = 3
34.
=>
AQ = (3 x 4) / 5 = 12/5 = 2,4
b. Zandloper:
=>
BS = (3 x 2) / 4 = 6/4 = 1,5
c. UT ≈ 0,78
35.
AB2 = 14400
AB = √14400
AB = 120
Bereken nu BC (lengte stok):
AB2 + AC2 = BC2
1202 + 502 = BC2
BC2 = 16900
BC = √16900
BC = 130
Driehoek ABC ∼ driehoek DEC (i.v.m. snavelfiguur)
=>
We krijgen het volgende kruisproduct:
DC = (26 x 50) / 130 = 10
AD = AC - DC = 50 - 10 = 40
Dus hoogte van het water is 40 cm.
Inhoud water = l x b x h = 96 x 72 x 40 = 276 480cm3.
Dat is 276,5 liter
Tip:
Stel DE = x
Bereken eerst DE en dan DG.
Zonnestralen zijn evenwijdig, dus ∠B = ∠C i.v.m. F-hoeken
Driehoek BDF ∼ driehoek CDEStel DE = x
Bereken eerst DE en dan DG.
Zonnestralen zijn evenwijdig, dus ∠B = ∠C i.v.m. F-hoeken
| driehoek BDF | BD | DF | BF |
| driehoek CDE | CD | DE | CE |
=>
| 424,8 | (x + 32) | BF |
| 367,2 | x | CE |
x ⋅ 424,8 = 367,2 ⋅ (x + 32)
424,8x = 367,2x + 11750,4
57,6x = 11750,4
x = 204
Dus DE = 204
Driehoek ADG ∼ driehoek CDE
| driehoek ADG | AD | DG | AG |
| driehoek CDE | CD | DE | CE |
=>
| 655,2 | DG | AG |
| 367,2 | 204 | CE |
DG = (655,2 x 204) / 367,2 = 364
Dus hoogte van de toren is 364 meter.

30.
Tip:
Stel DS = x dan is ES = (13 - x)
DE2 = CE2 + CD2Stel DS = x dan is ES = (13 - x)
DE2 = 52 + 122
DE2 = 169
DE = √169 = 13
Driehoek ASD ∼ driehoek CSE (i.v.m. zandloperfiguur)
| driehoek ASD | AS | SD | AD |
| driehoek CSE | CS | SE | CE |
=>
| AS | x | 7 |
| CS | (13 - x) | 5 |
7 ⋅ (13 - x) = 5 ⋅ x
91 - 7x = 5x
-12x = -91
12x = 91
x = 91/12
x ≈ 7,58
x ≈ 7,6
Dus DS = 7,6
31.
Tip:
Bereken eerst BD met de Stelling van Pythagoras.
Stel DS = x dan is BS = (BD - x) = (20 - x)
Omdat het een trapezium is, zijn CD en AB evenwijdig. Dus we hebben een zandloper.
BD2 + BC2 = CD2Bereken eerst BD met de Stelling van Pythagoras.
Stel DS = x dan is BS = (BD - x) = (20 - x)
Omdat het een trapezium is, zijn CD en AB evenwijdig. Dus we hebben een zandloper.
BD2 + 152 = 252
BD2 = 400
BD = √400 = 20
Driehoek ABS ∼ driehoek CDS (i.v.m. zandloperfiguur)
| driehoek ABS | AB | BS | AS |
| driehoek CDS | CD | DS | CS |
=>
| 10 | (20 - x) | AS |
| 25 | x | CS |
We krijgen het volgende kruisproduct:
25(20 - x) = 10x
500 - 25x = 10x
-35x = -500
x = -500 / -35
x ≈ 14,3
Dus: BS = 20 - x = 20 - 14,3 = 5,7
32.
Tip:
Bij een schets hoeven de afmetingen niet te kloppen.
Bereken eerst EG met de Stelling van Pythagoras.
GS = 5 - 2 = 3
EH2 + GH2 = GE2Bij een schets hoeven de afmetingen niet te kloppen.
Bereken eerst EG met de Stelling van Pythagoras.
GS = 5 - 2 = 3
32 + 42 = GE2
GE2 = 25
GE = √25 = 5
GS = GE - ES = 5 - 2 = 3
Driehoek ESP ∼ driehoek GSC (i.v.m. zandloperfiguur)
| driehoek ESP | ES | SP | EP |
| driehoek GSC | GS | SC | GC |
=>
| 2 | SP | EP |
| 3 | SC | 4 |
We krijgen het volgende kruisproduct:
EP = (2 x 4) / 3 = 8/3 = 2 2/3

33.
Tip:
Bereken eerst EG met de Stelling van Pythagoras.
Bereken SG met snavelfiguur.
ES = EG - SG
AB2 + BC2 = AC2Bereken eerst EG met de Stelling van Pythagoras.
Bereken SG met snavelfiguur.
ES = EG - SG
62 + 4,52 = AC2
AC2 = 56,25
AC = √56,25
AC = 7,5
Dus EG = AC = 7,5
Driehoek ACQ ∼ driehoek SGQ (i.v.m. snavelfiguur)
| driehoek ACQ | AC | CQ | AQ |
| driehoek SGQ | SG | GQ | SQ |
=>
| 7,5 | 5 | AQ |
| SG | 3 | SQ |
We krijgen het volgende kruisproduct:
SG = (7,5 x 3) / 5 = 4,5
Dus: ES = EG - SG = 7,5 - 4,5 = 3

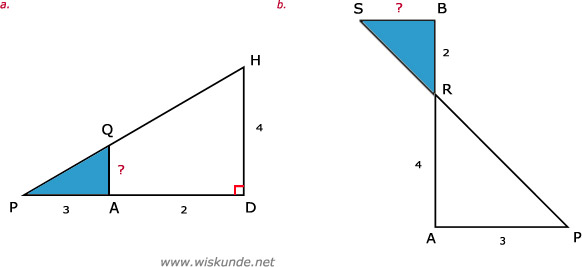
34.
Tip:
BR = AB - AR = 6 - 4 = 2
a. Snavel:BR = AB - AR = 6 - 4 = 2
| AP | AQ | PQ |
| DP | DH | HP |
| 3 | AQ | PQ |
| 5 | 4 | HP |
AQ = (3 x 4) / 5 = 12/5 = 2,4
b. Zandloper:
| AP | PR | AR |
| BS | RS | BR |
| 3 | PR | 4 |
| BS | RS | 2 |
BS = (3 x 2) / 4 = 6/4 = 1,5
c. UT ≈ 0,78

35.
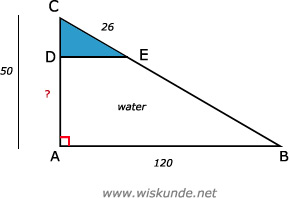
Tip:
BC is de hele stok
DE is de watergrens
Bereken eerst AD (hoogte water)
Bereken dan: Inhoud = lengte x breedte x hoogte = 96 x 72 x AD
AB2 = 722 + 962BC is de hele stok
DE is de watergrens
Bereken eerst AD (hoogte water)
Bereken dan: Inhoud = lengte x breedte x hoogte = 96 x 72 x AD
AB2 = 14400
AB = √14400
AB = 120
Bereken nu BC (lengte stok):
AB2 + AC2 = BC2
1202 + 502 = BC2
BC2 = 16900
BC = √16900
BC = 130
Driehoek ABC ∼ driehoek DEC (i.v.m. snavelfiguur)
| driehoek ABC | AB | BC | AC |
| driehoek DEC | DE | EC | DC |
=>
| 120 | 130 | 50 |
| DE | 26 | DC |
We krijgen het volgende kruisproduct:
DC = (26 x 50) / 130 = 10
AD = AC - DC = 50 - 10 = 40
Dus hoogte van het water is 40 cm.
Inhoud water = l x b x h = 96 x 72 x 40 = 276 480cm3.
Dat is 276,5 liter

Andere paragrafen:
2.1. Gelijkvormige driehoeken (1 t/m 18)
2.2. Snavel- en zandloperfiguren (19 t/m 35)
2.3. Hellingsgetal (36 t/m 41)
2.4. De tangens (42 t/m 57)
2.5. Berekeningen met de tangens (58 t/m 72)
2.1. Gelijkvormige driehoeken (1 t/m 18)
2.2. Snavel- en zandloperfiguren (19 t/m 35)
2.3. Hellingsgetal (36 t/m 41)
2.4. De tangens (42 t/m 57)
2.5. Berekeningen met de tangens (58 t/m 72)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


