TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.4 De tangens VWO 3
Boek: Getal & Ruimte - Gelijkvormigheid VWO 3 (deel 1) opgaven 42 t/m 57, 2011Om de hellingshoek te berekenen, gebruiken we de tangens (tan).
De tangens van een hellingshoek = verticale verplaatsing / horizontale verplaatsing
De tangens van hoek A schrijven we: tan(∠A).
Lees meer over de tangens
De tangens van een hellingshoek = verticale verplaatsing / horizontale verplaatsing
De tangens van hoek A schrijven we: tan(∠A).
Lees meer over de tangens
42.
hellingsgetal = verticale verplaatsing / horizontale verplaatsing = 3/5 = 0,6
b. Bij een horizontale verplaatsing van 10 cm krijgen we een verticale verplaatsing van 6 cm.
hellingsgetal = verticale verplaatsing / horizontale verplaatsing = 6/10 = 0,6
c. Bij een horizontale verplaatsing van 12 cm krijgen we een verticale verplaatsing van 7,2 cm.
hellingsgetal = verticale verplaatsing / horizontale verplaatsing = 7,2/12 = 0,6
43.
b. ≈ 0,07
c. ≈ 0,84
d. ≈ 0,27
e. ≈ 0,02
f. ≈ 57,29
44.
Dus het hellingsgetal = 0,14
Dus hellingspercentage = 14%, dus bord d.
45.
a. ≈ 0,00
b. ≈ 52,31
c. ≈ 53,04
d. ≈ 12,10
e. ≈ 1,17
f. ≈ -0,27
g. ≈ 5,66
h. ≈ 8,95
i. ≈ 3,08
46.
BC = tan(18º) x 450
BC ≈ 146
Dus de verticale verplaatsing is 146 m.
b. tan(22º) = 63 / AB
AB = 63 / tan(22º)
AB ≈ 156
Dus de horizontale verplaatsing is 156 m.
47.
De verticale verplaatsing is: AC
De horizontale verplaatsing is: AB
b.
tan(22º) = verticale verplaatsing / horizontale verplaatsing = AC/AB
tan(22º) = AC / 4,5
AC = tan(22º) x 4,5
AC ≈ 1,8 cm
48.
tan(15º) = verticale verplaatsing / horizontale verplaatsing = BC/AB
tan(15º) = BC / 98
BC = tan(15º) x 98
BC ≈ 26,3 m
b.
AB2 + BC2 = AC2
982 + 26,32 = AC2
AC2 = 10295,69
AC = √10295,69
AC ≈ 101,5 m
c.
Oppervlakte = lengte x breedte
Oppervlakte = 24 x 101,5
Oppervlakte = 2436 m2
49.
tan(59º) = verticale verplaatsing / horizontale verplaatsing = h / 55
h = tan(59º) x 55
h = 91,5 cm
Afgerond op gehelen: 92 cm
b.
Bereken de lengte van AC.
AD2 + CD2 = AC2
552 + 922 = AC2
AC2 = 11 489
AC = √11 489
AC ≈ 107 cm
50.
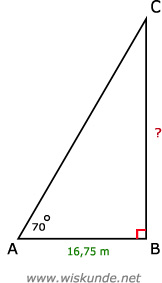
tan(70º) = verticale verplaatsing / horizontale verplaatsing = BC / AB
tan(70º) = BC / 16,75
BC = tan(70º) x 16,75
BC ≈ 46,0 m
b.
Bereken eerst de lengte van AC.
AB2 + BC2 = AC2
16,752 + 46,02 = AC2
AC2 = 2396,5625
AC = √2396,5625
AC ≈ 48,95 m
AC ≈ 49 m
In 44 sec. leg je 49 meter af. Dat is in 1 sec. dus 1,1136 meter (49/44).
1,1136 m/s x 3,6 = 4,0 km/uur.
51.
a. hellingspercentage = 85% -> hellingshoek ≈ 40º
b. hellingspercentage = 25% -> hellingshoek ≈ 14º
c. hellingspercentage = 55% -> hellingshoek ≈ 28º
d. hellingspercentage = 100% -> hellingshoek ≈ 45º
Tip:
De verhouding verticaal/horizontaal is steeds gelijk.
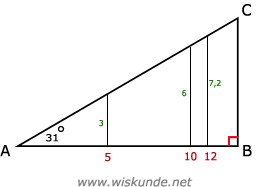
a. Bij een horizontale verplaatsing van 5 cm krijgen we een verticale verplaatsing van 3 cm.De verhouding verticaal/horizontaal is steeds gelijk.
hellingsgetal = verticale verplaatsing / horizontale verplaatsing = 3/5 = 0,6
b. Bij een horizontale verplaatsing van 10 cm krijgen we een verticale verplaatsing van 6 cm.
hellingsgetal = verticale verplaatsing / horizontale verplaatsing = 6/10 = 0,6
c. Bij een horizontale verplaatsing van 12 cm krijgen we een verticale verplaatsing van 7,2 cm.
hellingsgetal = verticale verplaatsing / horizontale verplaatsing = 7,2/12 = 0,6

43.
Tip:
Zorg ervoor dat je rekenmachine bij de instellingen op DEG staat.
a. ≈ 0,53Zorg ervoor dat je rekenmachine bij de instellingen op DEG staat.
b. ≈ 0,07
c. ≈ 0,84
d. ≈ 0,27
e. ≈ 0,02
f. ≈ 57,29
44.
Tip:
hellingspercentage = tan(hellingshoek) x 100%
tan(8º) ≈ 0,14hellingspercentage = tan(hellingshoek) x 100%
Dus het hellingsgetal = 0,14
Dus hellingspercentage = 14%, dus bord d.
45.
a. ≈ 0,00
b. ≈ 52,31
c. ≈ 53,04
d. ≈ 12,10
e. ≈ 1,17
f. ≈ -0,27
g. ≈ 5,66
h. ≈ 8,95
i. ≈ 3,08
46.
Tip:
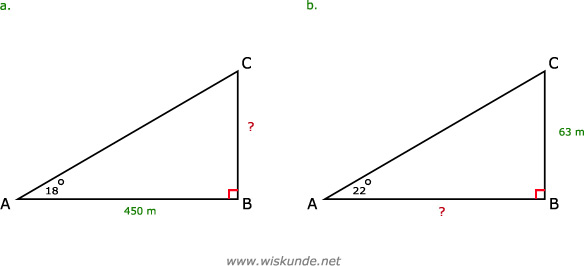
a. tan(18º) = BC / 450| hellingsgetal | verticale verplaatsing |
| 1 | horizontale verplaatsing |
BC = tan(18º) x 450
BC ≈ 146
Dus de verticale verplaatsing is 146 m.
b. tan(22º) = 63 / AB
AB = 63 / tan(22º)
AB ≈ 156
Dus de horizontale verplaatsing is 156 m.

47.
Tip:
tan = verticaal / horizontaal = v / h
a. tan = verticaal / horizontaal = v / h
De verticale verplaatsing is: AC
De horizontale verplaatsing is: AB
b.
tan(22º) = verticale verplaatsing / horizontale verplaatsing = AC/AB
tan(22º) = AC / 4,5
AC = tan(22º) x 4,5
AC ≈ 1,8 cm
48.
Tip:
Als je BC weet, bereken dan AC met de Stelling van Pythagoras.
a.Als je BC weet, bereken dan AC met de Stelling van Pythagoras.
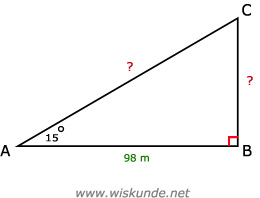
tan(15º) = verticale verplaatsing / horizontale verplaatsing = BC/AB
tan(15º) = BC / 98
BC = tan(15º) x 98
BC ≈ 26,3 m
b.
AB2 + BC2 = AC2
982 + 26,32 = AC2
AC2 = 10295,69
AC = √10295,69
AC ≈ 101,5 m
c.
Oppervlakte = lengte x breedte
Oppervlakte = 24 x 101,5
Oppervlakte = 2436 m2

49.
Tip:
Maak een schets van de situatie.
AC is 1 van de 4 delen die even lang zijn.
AC kan met de Stelling van Pythagoras.
a.Maak een schets van de situatie.
AC is 1 van de 4 delen die even lang zijn.
AC kan met de Stelling van Pythagoras.
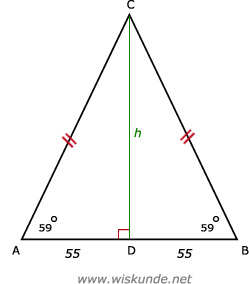
tan(59º) = verticale verplaatsing / horizontale verplaatsing = h / 55
h = tan(59º) x 55
h = 91,5 cm
Afgerond op gehelen: 92 cm
b.
Bereken de lengte van AC.
AD2 + CD2 = AC2
552 + 922 = AC2
AC2 = 11 489
AC = √11 489
AC ≈ 107 cm

50.
Tip:
Bij b.: Bereken eerst de lengte van AC met de Stelling van Pythagoras.
Van m/s naar km/uur => x3,6
a.Bij b.: Bereken eerst de lengte van AC met de Stelling van Pythagoras.
Van m/s naar km/uur => x3,6
tan(70º) = verticale verplaatsing / horizontale verplaatsing = BC / AB
tan(70º) = BC / 16,75
BC = tan(70º) x 16,75
BC ≈ 46,0 m
b.
Bereken eerst de lengte van AC.
AB2 + BC2 = AC2
16,752 + 46,02 = AC2
AC2 = 2396,5625
AC = √2396,5625
AC ≈ 48,95 m
AC ≈ 49 m
In 44 sec. leg je 49 meter af. Dat is in 1 sec. dus 1,1136 meter (49/44).
1,1136 m/s x 3,6 = 4,0 km/uur.

51.
a. hellingspercentage = 85% -> hellingshoek ≈ 40º
b. hellingspercentage = 25% -> hellingshoek ≈ 14º
c. hellingspercentage = 55% -> hellingshoek ≈ 28º
d. hellingspercentage = 100% -> hellingshoek ≈ 45º
52.
a. 62,1º
b. 39,4º
c. 33,7º
d. 84,1º
e. 37,9º
f. 45º
g. 69,3º
h. 66,9º
i. 77,0º
53.
54.
∠A = tan-1(22 / 40)
∠A ≈ 28,8º
tan(∠B) = 29 / 39
∠B = tan-1(29 / 39)
∠B ≈ 36,6º
tan(∠C) = 36 / 28
∠C = tan-1(36 / 28)
∠C ≈ 52,1º
55.
b. hoek = tan-1(0,08) ≈ 4,6º
c. hoek = tan-1( 2 / 7 ) ≈ 16,0º
d. hoek = tan-1(0,14) ≈ 8,0º
56.
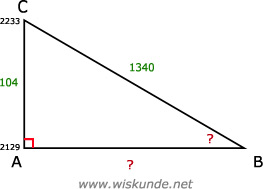
AB2 + AC2 = BC2
AB2 + 1042 = 13402
AB2 = 1784784
AB = √1784784
AB ≈ 1335,96 m
tan(∠B) = verticale verplaatsing / horizontale verplaatsing = AC / AB
∠B = tan-1(104 / 1335,96)
∠B ≈ 4,45º
57.
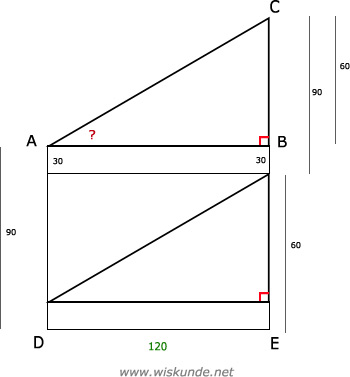
BC = EC - AD
BC = (90 + 4x15) - 90
BC = 150 - 90
BC = 60
tan(∠A) = verticale verplaatsing / horizontale verplaatsing = BC / AB
tan(∠A) = 60 / 120 = 1/2
∠A = tan-1(0,5)
∠A ≈ 26,6º
b.
AC is de lengte van de trapleuning.
AB2 + BC2 = AC2
1202 + 602 = AC2
AC2 = 18000
AC = √18000
AC ≈ 134,16 m
Dus de trapleuning is 134,2 cm.
a. 62,1º
b. 39,4º
c. 33,7º
d. 84,1º
e. 37,9º
f. 45º
g. 69,3º
h. 66,9º
i. 77,0º
53.
Tip:
Als hellingsgetal = 0,2 dan is de hellingshoek: tan-1(0,2) ≈ 11,3º
Als hellingshoek = 17º dan is het hellingsgetal: tan(17º) ≈ 0,3
Als hellingsgetal = 0,2 dan is de hellingshoek: tan-1(0,2) ≈ 11,3º
Als hellingshoek = 17º dan is het hellingsgetal: tan(17º) ≈ 0,3
| hellingshoek | 11,3 º | 17 º | 69,7 º | 5 º | 71,0 º | 39 º | 77,5 º | 79,5 º | 80,2 º |
| hellingsgetal | 0,2 | 0,3 | 2,7 | 0,1 | 2,9 | 0,8 | 4,5 | 5,4 | 5,8 |
54.
Tip:
Ezelsbruggetje: om de hoek in graden te krijgen, gebruik je de tan-1.
Bedenk dat het graden teken (...º) en inverse teken (...-1) dan bij elkaar horen.
Dus (º) en (-1) zijn vriendjes.
tan(∠A) = 22 / 40Ezelsbruggetje: om de hoek in graden te krijgen, gebruik je de tan-1.
Bedenk dat het graden teken (...º) en inverse teken (...-1) dan bij elkaar horen.
Dus (º) en (-1) zijn vriendjes.
∠A = tan-1(22 / 40)
∠A ≈ 28,8º
tan(∠B) = 29 / 39
∠B = tan-1(29 / 39)
∠B ≈ 36,6º
tan(∠C) = 36 / 28
∠C = tan-1(36 / 28)
∠C ≈ 52,1º
55.
Tip:
hellingspercentage = tan(hellingshoek) x 100%
a. hoek = tan-1( 1 / 10 ) ≈ 5,7ºhellingspercentage = tan(hellingshoek) x 100%
b. hoek = tan-1(0,08) ≈ 4,6º
c. hoek = tan-1( 2 / 7 ) ≈ 16,0º
d. hoek = tan-1(0,14) ≈ 8,0º
56.
Tip:
Bereken eerst AB en gebruik daarna de tangens.
Bereken de lengte van AB (horizontaal).Bereken eerst AB en gebruik daarna de tangens.
AB2 + AC2 = BC2
AB2 + 1042 = 13402
AB2 = 1784784
AB = √1784784
AB ≈ 1335,96 m
tan(∠B) = verticale verplaatsing / horizontale verplaatsing = AC / AB
∠B = tan-1(104 / 1335,96)
∠B ≈ 4,45º

57.
Tip:
Maak eerst een goede schets. Bereken dan BC.
a.Maak eerst een goede schets. Bereken dan BC.
BC = EC - AD
BC = (90 + 4x15) - 90
BC = 150 - 90
BC = 60
tan(∠A) = verticale verplaatsing / horizontale verplaatsing = BC / AB
tan(∠A) = 60 / 120 = 1/2
∠A = tan-1(0,5)
∠A ≈ 26,6º
b.
AC is de lengte van de trapleuning.
AB2 + BC2 = AC2
1202 + 602 = AC2
AC2 = 18000
AC = √18000
AC ≈ 134,16 m
Dus de trapleuning is 134,2 cm.

Andere paragrafen:
2.1. Gelijkvormige driehoeken (1 t/m 18)
2.2. Snavel- en zandloperfiguren (19 t/m 35)
2.3. Hellingsgetal (36 t/m 41)
2.4. De tangens (42 t/m 57)
2.5. Berekeningen met de tangens (58 t/m 72)
2.1. Gelijkvormige driehoeken (1 t/m 18)
2.2. Snavel- en zandloperfiguren (19 t/m 35)
2.3. Hellingsgetal (36 t/m 41)
2.4. De tangens (42 t/m 57)
2.5. Berekeningen met de tangens (58 t/m 72)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


