TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.1 Rechthoekige driehoeken HAVO/VWO 2
Boek: Getal & Ruimte - De stelling van Pythagoras HAVO/VWO 2 (deel 2) opgaven 1 t/m 9, 2010De stelling van Pythagoras is als volgt:
In elke rechthoekige driehoek geldt dat: de ene rechthoekszijde in het kwadraat + de andere rechthoekszijde in het kwadraat is gelijk aan de schuine zijde in het kwadraat. Meer wiskundig: a2 + b2 = c2
Bedenk wel dat de Stelling van Pythagoras alleen geldt in driehoeken die een rechte hoek hebben.
De kwadraten in de stelling staan voor de vierkanten die je op elke zijde kunt plaatsen.
De som van de oppervlakten van de twee kleinste vierkanten is dan gelijk aan de oppervlakte van het vierkant aan de schuine zijde.
In elke rechthoekige driehoek geldt dat: de ene rechthoekszijde in het kwadraat + de andere rechthoekszijde in het kwadraat is gelijk aan de schuine zijde in het kwadraat. Meer wiskundig: a2 + b2 = c2
Bedenk wel dat de Stelling van Pythagoras alleen geldt in driehoeken die een rechte hoek hebben.
De kwadraten in de stelling staan voor de vierkanten die je op elke zijde kunt plaatsen.
De som van de oppervlakten van de twee kleinste vierkanten is dan gelijk aan de oppervlakte van het vierkant aan de schuine zijde.
1.
b. Linksboven heeft 16 hokjes, rechtsboven 9. Het grote vierkant 25.
c. De som van het aantal vierkantjes van de 2 kleine is gelijk aan het aantal vierkantjes van het grote vierkant.

2.
b. oppervlakte van het rode vierkant: 50 + 17 = 67 mm2
c. oppervlakte van het rode vierkant: 140 - 120 = 20 mm2
d. oppervlakte van het rode vierkant: 72 - 30 = 42 mm2
3.
b. Het rode driehoek heeft een oppervlakte: 1/2 * basis * hoogte. We hebben 4 van die driehoeken. Namelijk een rode en 3 witte. Dit levert: 4 * 1/2 * a * b. Tellen we daar vierkant III bij op (opp c2) dan krijg je opp(PQRS) = 4 * 1/2 * a * b + c2.
c. We hebben dus 2 manieren gevonden voor de oppervlakte van vierkant PQRS. Manier 1 was (a+b)2 en manier 2 was 4 * 1/2 * a * b + c2. Deze zijn dus gelijk aan elkaar. Dit levert:
(a+b)2 = 4 * 1/2 * a * b + c2
Als we dit verder uitwerken, dan:
(a+b)(a+b) = 4 * 1/2 * a * b + c2
a2 + ab + ab + b2 = 2ab + c2
a2 + 2ab + b2 = 2ab + c2
Als je nu links en rechts -2ab doet, dan krijgen we:
a2 + b2 = c2
d. opp I = b2, opp II = a2, opp III = c2, dus opp I + opp II = opp III
4.
b. √83 ≈ 9,1 mm. Dat is 0,9 cm.
c. √600 ≈ 24,5 dm. Dat is 245 cm.
5.
Opp (I) = 1,62 = 2,56 cm2
Opp (II) = 2,42 = 5,76 cm2
Opp (III) = Opp (I) + Opp (II) = 2,56 + 5,76 = 8,32 cm2
b. BC = √ 8,32 ≈ 2,9 cm
6.
b. PR2 + QR2 = PQ2
c. KL2 + LM2 = KM2
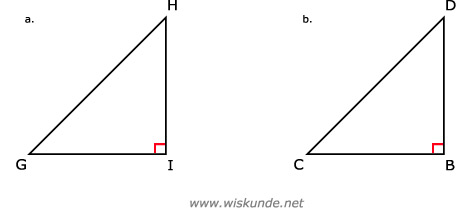
7.
b. BC2 + BD2 = CD2
8.
b. AB2 + BC2 = AC2
AD2 + BD2 = AB2
BD2 + CD2 = BC2
9.
AB2 + AD2 = BD2
Tip:
De oppervlakte van een vierkant is gelijk aan de zijde in het kwadraat.
a. De witte driehoek is een rechthoekige driehoekDe oppervlakte van een vierkant is gelijk aan de zijde in het kwadraat.
b. Linksboven heeft 16 hokjes, rechtsboven 9. Het grote vierkant 25.
c. De som van het aantal vierkantjes van de 2 kleine is gelijk aan het aantal vierkantjes van het grote vierkant.

2.
Tip:
De som van de oppervlakten van de twee kleinste vierkanten is gelijk aan de oppervlakte van het grootste vierkant.
a. oppervlakte van het rode vierkant: 90 + 35 = 125 mm2De som van de oppervlakten van de twee kleinste vierkanten is gelijk aan de oppervlakte van het grootste vierkant.
b. oppervlakte van het rode vierkant: 50 + 17 = 67 mm2
c. oppervlakte van het rode vierkant: 140 - 120 = 20 mm2
d. oppervlakte van het rode vierkant: 72 - 30 = 42 mm2
3.
Tip:
oppervlakte driehoek = ½ x basis x hoogte
a. Het vierkant PQRS heeft als zijde (a+b). De oppervlakte van een vierkant is de zijde in het kwadraat. Vandaar dus (a+b)2.oppervlakte driehoek = ½ x basis x hoogte
b. Het rode driehoek heeft een oppervlakte: 1/2 * basis * hoogte. We hebben 4 van die driehoeken. Namelijk een rode en 3 witte. Dit levert: 4 * 1/2 * a * b. Tellen we daar vierkant III bij op (opp c2) dan krijg je opp(PQRS) = 4 * 1/2 * a * b + c2.
c. We hebben dus 2 manieren gevonden voor de oppervlakte van vierkant PQRS. Manier 1 was (a+b)2 en manier 2 was 4 * 1/2 * a * b + c2. Deze zijn dus gelijk aan elkaar. Dit levert:
(a+b)2 = 4 * 1/2 * a * b + c2
Als we dit verder uitwerken, dan:
(a+b)(a+b) = 4 * 1/2 * a * b + c2
a2 + ab + ab + b2 = 2ab + c2
a2 + 2ab + b2 = 2ab + c2
Als je nu links en rechts -2ab doet, dan krijgen we:
a2 + b2 = c2
d. opp I = b2, opp II = a2, opp III = c2, dus opp I + opp II = opp III
4.
Tip:
Een vierkant met oppervlakte a heeft zijde √a.
Dus een vierkant met oppervlakte gelijk aan 9 heeft een zijde van √9. En dat is dus gelijk aan 3.
En dat klopt, want 3 x 3 = 9
a. √8,3 ≈ 2,9 cm.Een vierkant met oppervlakte a heeft zijde √a.
Dus een vierkant met oppervlakte gelijk aan 9 heeft een zijde van √9. En dat is dus gelijk aan 3.
En dat klopt, want 3 x 3 = 9
b. √83 ≈ 9,1 mm. Dat is 0,9 cm.
c. √600 ≈ 24,5 dm. Dat is 245 cm.
5.
Tip:
Neem voor lengte BC de wortel uit de oppervlakte van vierkant III.
a.Neem voor lengte BC de wortel uit de oppervlakte van vierkant III.
Opp (I) = 1,62 = 2,56 cm2
Opp (II) = 2,42 = 5,76 cm2
Opp (III) = Opp (I) + Opp (II) = 2,56 + 5,76 = 8,32 cm2
b. BC = √ 8,32 ≈ 2,9 cm
6.
Tip:
De ene rechthoekszijde in het kwadraat + de andere rechthoekszijde in het kwadraat is gelijk aan de schuine zijde in het kwadraat.
a. DE2 + DF2 = EF2De ene rechthoekszijde in het kwadraat + de andere rechthoekszijde in het kwadraat is gelijk aan de schuine zijde in het kwadraat.
b. PR2 + QR2 = PQ2
c. KL2 + LM2 = KM2
7.
Tip:
Maak een schets. Dan zie je het beter.
a. GI2 + HI2 = GH2Maak een schets. Dan zie je het beter.
b. BC2 + BD2 = CD2

8.
Tip:
AB ligt horizontaal. Maar is wel de schuine zijde van driehoek ABD.
BC ligt verticaal. Maar is wel de schuine zijde van driehoek BCD.
a. Driehoeken ABC, ABD, BCDAB ligt horizontaal. Maar is wel de schuine zijde van driehoek ABD.
BC ligt verticaal. Maar is wel de schuine zijde van driehoek BCD.
b. AB2 + BC2 = AC2
AD2 + BD2 = AB2
BD2 + CD2 = BC2
9.
Tip:
Driehoek ABE is NIET rechthoekig!
AB2 + BC2 = AC2 Driehoek ABE is NIET rechthoekig!
AB2 + AD2 = BD2
Andere paragrafen:
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 41)
6.4. Pythagoras in de ruimte (42 t/m 52)
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 41)
6.4. Pythagoras in de ruimte (42 t/m 52)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


