Uitwerking 3.1 Kwadratische formules opgave 8
01-07-2025
admin
Getal & Ruimte HAVO 3 (deel 1) hoofdstuk 3 Kwadratische problemen
Uitleg
Tip: let op -x2. Als je daar bijv. -1 invult, zet dan haakjes om de x. Dus -(x)2. Vul dan voor x = -1 in.
Dan krijg je -(-1)2. Reken eerst het kwadraat uit. Dat geeft -(1). Uitkomst is dus -1.
Vraag 8
Gegeven is de formule y = -x2 + 4x.
a. Reken na dat bij x = -1 hoort y = -5.
b. Vul de tabel in.
c. Teken de grafiek.
Antwoord
a.
Vul voor x het getal -1 in. Dit levert: y = -(-1)2 + 4 ⋅ -1 = -(1) + -4 = -1 - 4 = -5
b.
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | -5 | 0 | 3 | 4 | 3 | 0 | -5 |
Uitwerking
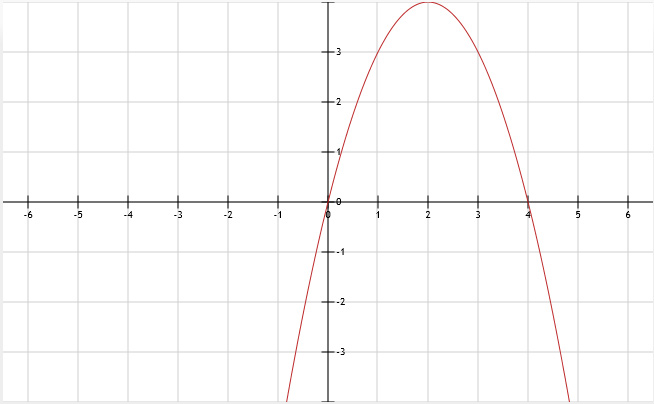
b.
Vul de waarde van x in in de vergelijking.
Vul voor x het getal -1 in. Dit levert: y = -(-1)2 + (4 ⋅ -1) = -(1) + (-4) = -1 - 4 = -5
Vul voor x het getal 0 in. Dit levert: y = -(0)2 + (4 ⋅ 0) = -(0) + (0) = 0
Vul voor x het getal 1 in. Dit levert: y = -(1)2 + (4 ⋅ 1) = -(1) + (4) = -1 + 4 = 3
Vul voor x het getal 2 in. Dit levert: y = -(2)2 + (4 ⋅ 2) = -(4) + (8) = -4 + 8 = 4
Vul voor x het getal 3 in. Dit levert: y = -(3)2 + (4 ⋅ 3) = -(9) + (12) = -9 + 12 = 3
Vul voor x het getal 4 in. Dit levert: y = -(4)2 + (4 ⋅ 4) = -(16) + (16) = -16 + 16 = 0
Vul voor x het getal 5 in. Dit levert: y = -(5)2 + (4 ⋅ 5) = -(25) + (20) = -25 + 20 = -5
Reageer op deze uitwerking
Heb je een vraag over deze opgave, snap je iets niet of ben je een fout tegengekomen en wil je binnen 10 minuten antwoord? Stel een vraag!