TIP: Wil je ook toegang tot meer dan 16.900 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 7.3 Bijzondere ongelijkheden VWO 3
Boek: Getal & Ruimte - Ongelijkheden en parabolen VWO 3 (deel 2) opgaven 23 t/m 37, 2011Ongelijkheden oplossen met de abc-formule en Discriminant:
D > 0, dan zijn er 2 oplossingen en dus 2 snijpunten met de x-as
D = 0, dan is er 1 oplossing en dus 1 snijpunt met de x-as (raakpunt)
D < 0, dan zijn er 0 oplossingen en dus geen snijpunten met de x-as
Meer info over de abc formule...
D > 0, dan zijn er 2 oplossingen en dus 2 snijpunten met de x-as
D = 0, dan is er 1 oplossing en dus 1 snijpunt met de x-as (raakpunt)
D < 0, dan zijn er 0 oplossingen en dus geen snijpunten met de x-as
Meer info over de abc formule...
23.
a. Met de abc-formule zie je dat D = -8. Dan zijn er geen nulpunten, dus geen oplossingen.
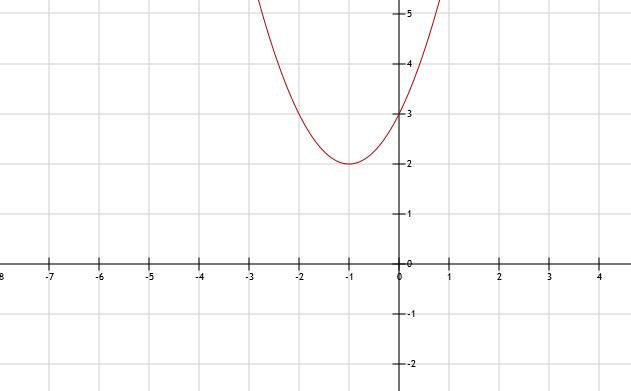
b. Zie afbeelding. Je ziet dat er geen snijpunten zijn met de x-as.
c. Je ziet dat voor elke denkbare x, de functiewaarde (ofwel de y-waarde) boven de x-as ligt.
24.
a. Voor elke x ligt de y-waarde van de functie f onder de lijn y = 0 (ofwel de x-as)
b. Voor geen enkele x
c. Voor elke x ligt de y-waarde van de functie f onder de lijn y = 3
25.
a. Voor geen enkele x geldt g(x) < 0 (de functie g ligt nergens onder de x-as)
b. Voor elke x (behalve -4) geldt g(x) > 0
c. Voor geen enkele x geldt g(x) < -3
26.
a. Voor elke x (behalve 2) geldt h(x) < 0
b. Voor geen enkele x geldt h(x) > 0
c. Voor elke x geldt h(x) < 2 (de functie h ligt altijd onder de lijn y = 2)
27.
a. Met abc-formule D = -8, dus er zijn geen oplossingen
b. Met abc-formule D = -4, dus er zijn geen oplossingen
c. Met abc-formule D = -68, dus er zijn geen oplossingen
d. Met abc-formule D = -7, dus er zijn geen oplossingen
e. (x - 2)(x - 2) = 0, dus x = 2. De grafiek is een dalparabool die de x-as raakt in (2,0). Dus f(x) > 0 voor elke x ongelijk 2.
f. Geen oplossingen. Zie b.
28.
a. f(x) > 0 geen oplossingen. De grafiek ligt nergens boven de x-as. Grafiek is een bergparabool en raakt in (3,0)
b. Uit a volgt dat f(x) < 0 voor elke x, behalve x = 3
c. f(x) > 0 voor x ≠ ⅓
d. D = -3, dus geen oplossingen. De grafiek is een dalparabool die de x-as niet snijdt. Dus f(x) > 0 voor elke x
e. f(x) > 0 levert x < 0 v x > 1/2
f. x2 = -81, dus geen oplossingen. De grafiek is een dalparabool die de x-as niet snijdt. Dus f(x) > 0 voor elke x
29.
a. f(x) > 0 voor geen enkele x
b. f(x) > 0 voor elke x
c. f(x) < 0 voor geen enkele x
d. f(x) < 0 voor geen enkele x
e. f(x) > 0 voor geen enkele x
f. f(x) < 0 voor geen enkele x
30.
a. x2 < -3
b. x2 - 6x + 8 < 0
c. x2 > -16
d. (x + 6)2 > 0
e. x2 > 9
31.
a. Geen oplossingen als D < 0. Met abc-formule: a = 1, b = p en c = -3p.
Dus D = p2 + 12p. Voor welke p is D < 0? Dus p2 + 12p < 0.
f(p) = 0 voor p = 0 of p = -12.
D < 0 geeft -12 < p < 0. Dus de vergelijking x2 + px - 3p = 0 heeft geen oplossingen als je voor p een getal kiest tussen -12 en 0.
b. D < 0 geeft 0 < p < 4.
Dus de vergelijking x2 - 3px + 9p = 0 heeft geen oplossingen als je voor p een getal kiest tussen 0 en 4.
32.
Twee oplossingen, dus D > 0
a. D = p2 - 4p - 12. Nulpunten bij p = -2 of p = 6
D > 0 geeft p < -2 v p > 6
Dus de vergelijking heeft 2 oplossingen als je p een waarde geeft kleiner dan -2 of groter dan 6.
b. D = p2 + 10p + 16. Nulpunten bij p = -2 of p = -8
D > 0 geeft p < -8 v p > -2
Dus de vergelijking heeft 2 oplossingen als je p een waarde geeft kleiner dan -8 of groter dan -2.
a. Met de abc-formule zie je dat D = -8. Dan zijn er geen nulpunten, dus geen oplossingen.
b. Zie afbeelding. Je ziet dat er geen snijpunten zijn met de x-as.
c. Je ziet dat voor elke denkbare x, de functiewaarde (ofwel de y-waarde) boven de x-as ligt.

24.
a. Voor elke x ligt de y-waarde van de functie f onder de lijn y = 0 (ofwel de x-as)
b. Voor geen enkele x
c. Voor elke x ligt de y-waarde van de functie f onder de lijn y = 3
25.
a. Voor geen enkele x geldt g(x) < 0 (de functie g ligt nergens onder de x-as)
b. Voor elke x (behalve -4) geldt g(x) > 0
c. Voor geen enkele x geldt g(x) < -3
26.
a. Voor elke x (behalve 2) geldt h(x) < 0
b. Voor geen enkele x geldt h(x) > 0
c. Voor elke x geldt h(x) < 2 (de functie h ligt altijd onder de lijn y = 2)
27.
a. Met abc-formule D = -8, dus er zijn geen oplossingen
b. Met abc-formule D = -4, dus er zijn geen oplossingen
c. Met abc-formule D = -68, dus er zijn geen oplossingen
d. Met abc-formule D = -7, dus er zijn geen oplossingen
e. (x - 2)(x - 2) = 0, dus x = 2. De grafiek is een dalparabool die de x-as raakt in (2,0). Dus f(x) > 0 voor elke x ongelijk 2.
f. Geen oplossingen. Zie b.
28.
a. f(x) > 0 geen oplossingen. De grafiek ligt nergens boven de x-as. Grafiek is een bergparabool en raakt in (3,0)
b. Uit a volgt dat f(x) < 0 voor elke x, behalve x = 3
c. f(x) > 0 voor x ≠ ⅓
d. D = -3, dus geen oplossingen. De grafiek is een dalparabool die de x-as niet snijdt. Dus f(x) > 0 voor elke x
e. f(x) > 0 levert x < 0 v x > 1/2
f. x2 = -81, dus geen oplossingen. De grafiek is een dalparabool die de x-as niet snijdt. Dus f(x) > 0 voor elke x
29.
a. f(x) > 0 voor geen enkele x
b. f(x) > 0 voor elke x
c. f(x) < 0 voor geen enkele x
d. f(x) < 0 voor geen enkele x
e. f(x) > 0 voor geen enkele x
f. f(x) < 0 voor geen enkele x
30.
a. x2 < -3
b. x2 - 6x + 8 < 0
c. x2 > -16
d. (x + 6)2 > 0
e. x2 > 9
31.
a. Geen oplossingen als D < 0. Met abc-formule: a = 1, b = p en c = -3p.
Dus D = p2 + 12p. Voor welke p is D < 0? Dus p2 + 12p < 0.
f(p) = 0 voor p = 0 of p = -12.
D < 0 geeft -12 < p < 0. Dus de vergelijking x2 + px - 3p = 0 heeft geen oplossingen als je voor p een getal kiest tussen -12 en 0.
b. D < 0 geeft 0 < p < 4.
Dus de vergelijking x2 - 3px + 9p = 0 heeft geen oplossingen als je voor p een getal kiest tussen 0 en 4.
32.
Twee oplossingen, dus D > 0
a. D = p2 - 4p - 12. Nulpunten bij p = -2 of p = 6
D > 0 geeft p < -2 v p > 6
Dus de vergelijking heeft 2 oplossingen als je p een waarde geeft kleiner dan -2 of groter dan 6.
b. D = p2 + 10p + 16. Nulpunten bij p = -2 of p = -8
D > 0 geeft p < -8 v p > -2
Dus de vergelijking heeft 2 oplossingen als je p een waarde geeft kleiner dan -8 of groter dan -2.
33.
Stel op f(x) = g(x) en bepaal dan D.
D < 0 levert: -22 < p < -10, dus de 2 grafieken hebben geen snijpunten als je voor p een waarde kiest tussen -22 en -10.
34.
a. x < -2 v x > 2
b. -2 < x < 2
c. Voor elke x
d. Voor geen enkele x
35.
a. x < -6 v x > 6
b. -6 < x < 6
c. -√40 < x < √40
d. x < -12 v x > 12
e. -11 < x < 11
f. Elke x is een oplossing
g. x < -√24 v x > √24, nog kleiner: x < -2√6 v x > 2√6
h. x < -√48 v x > √48, nog kleiner: x < -4√3 v x > 4√3
36.
a. -√0,25 < x < √0,25 ofwel -0,5 < x < 0,5
b. x < -1 v x > 1
c. Elke x is een oplossing
d. Geen enkele x is een oplossing
e. -10 < x < 10
f. -√12 < x < √12 ofwel -2√3 < x < 2√3
g. x < -√0,01 v x > √0,01, ofwel x < -0,1 v x > 0,1
h. Voor elke x behalve x = 0
37.
a. Geen enkele x is een oplossing
b. Als c < 0, dan is geen enkele x een oplossing
c. x < -√c v x > √c
d. Elke x is een oplossing, behalve x = 0
e. Elke x is een oplossing
f. Elke x is een oplossing
Stel op f(x) = g(x) en bepaal dan D.
D < 0 levert: -22 < p < -10, dus de 2 grafieken hebben geen snijpunten als je voor p een waarde kiest tussen -22 en -10.
34.
a. x < -2 v x > 2
b. -2 < x < 2
c. Voor elke x
d. Voor geen enkele x
35.
a. x < -6 v x > 6
b. -6 < x < 6
c. -√40 < x < √40
d. x < -12 v x > 12
e. -11 < x < 11
f. Elke x is een oplossing
g. x < -√24 v x > √24, nog kleiner: x < -2√6 v x > 2√6
h. x < -√48 v x > √48, nog kleiner: x < -4√3 v x > 4√3
36.
a. -√0,25 < x < √0,25 ofwel -0,5 < x < 0,5
b. x < -1 v x > 1
c. Elke x is een oplossing
d. Geen enkele x is een oplossing
e. -10 < x < 10
f. -√12 < x < √12 ofwel -2√3 < x < 2√3
g. x < -√0,01 v x > √0,01, ofwel x < -0,1 v x > 0,1
h. Voor elke x behalve x = 0
37.
a. Geen enkele x is een oplossing
b. Als c < 0, dan is geen enkele x een oplossing
c. x < -√c v x > √c
d. Elke x is een oplossing, behalve x = 0
e. Elke x is een oplossing
f. Elke x is een oplossing
Andere paragrafen:
7.1. Ongelijkheden (1 t/m 9)
7.2. Kwadratische ongelijkheden (10 t/m 22)
7.3. Bijzondere ongelijkheden (23 t/m 37)
7.4. Parabolen verschuiven (38 t/m 54)
7.5. De top van een parabool (55 t/m 67)
7.1. Ongelijkheden (1 t/m 9)
7.2. Kwadratische ongelijkheden (10 t/m 22)
7.3. Bijzondere ongelijkheden (23 t/m 37)
7.4. Parabolen verschuiven (38 t/m 54)
7.5. De top van een parabool (55 t/m 67)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


