TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 5.1 Lineaire formules HAVO/VWO 2
Boek: Getal & Ruimte - Vergelijkingen HAVO/VWO 2 (deel 1) opgaven 1 t/m 16, 2011De basisformule voor een lijn is: y = ax + b, waarbij je voor a en b waarden kunt invullen.
Bedenk hierbij dat:
- a: 1 naar rechts is a omhoog
- b: de lijn de y-as snijdt in het punt (0,b)
Om een lijn te tekenen, heb je maar 2 punten nodig. Maak altijd een tabel. We noemen dit ook wel een visgraat.
Voorbeelden van lineaire formules zijn: y = -3x + 6 of N = 1/2t - 4
Teken een lijn altijd netjes met je geodriehoek.
Bedenk hierbij dat:
- a: 1 naar rechts is a omhoog
- b: de lijn de y-as snijdt in het punt (0,b)
Om een lijn te tekenen, heb je maar 2 punten nodig. Maak altijd een tabel. We noemen dit ook wel een visgraat.
Voorbeelden van lineaire formules zijn: y = -3x + 6 of N = 1/2t - 4
Teken een lijn altijd netjes met je geodriehoek.
1.
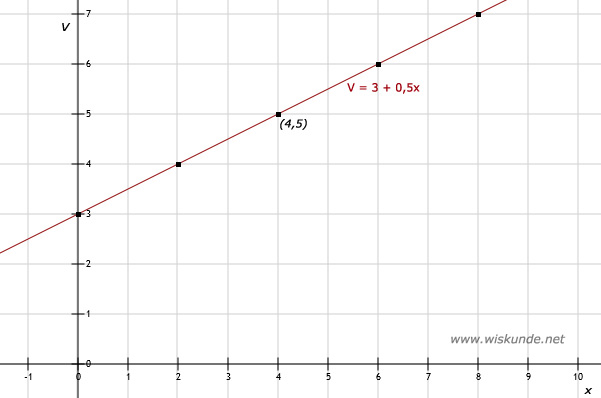
V = 3 + 0,5 ⋅ 6 = 3 + 3 = 6. Dus 6 euro;
V = 3 + 0,5 ⋅ 1,5 = 3 + 0,75 = 3,75. Dus 3,75 euro;
b.
c.
De punten op de grafiek zijn (zie tabel): (0,3), (2,4), (4,5), (6,6), (8,7) en (10,8).
d.
Prijs per kilometer is 0,5. Dus 50 eurocent.
2.
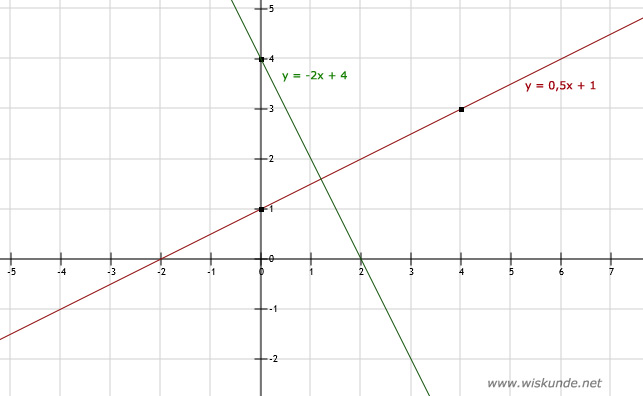
b.
3.
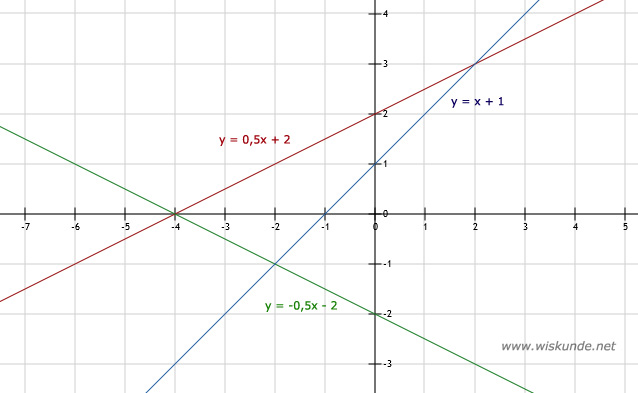
Zie afbeelding
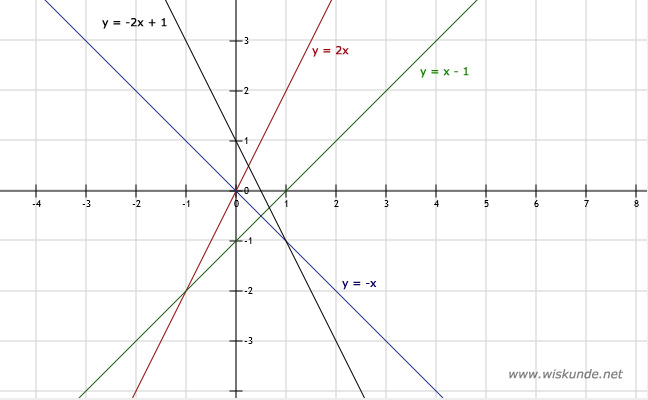
4.
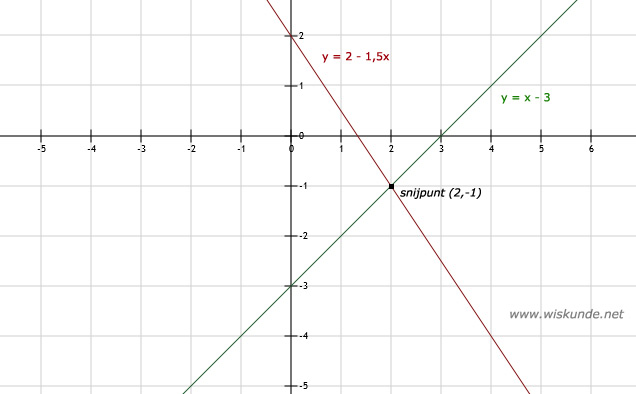
5.
b. Het snijpunt van deze 2 lijnen is: (2,-1)
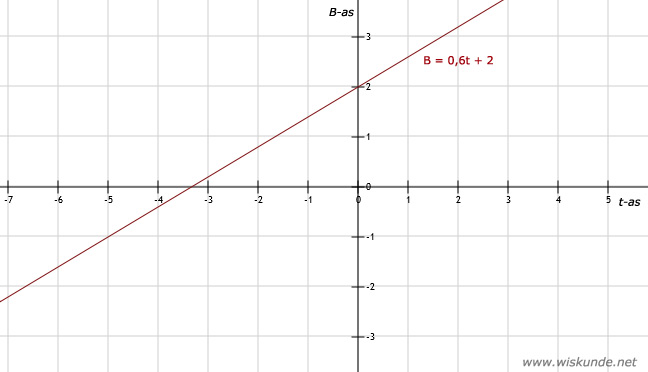
6.
b. Bij t = 2 krijg je als B-waarde 3,2. Dat tekent lastig in een assenstelsel want het is geen exact roosterpunt.
Nog een goede waarde is bij t = 10 of t = -5.
c. Zie afbeelding
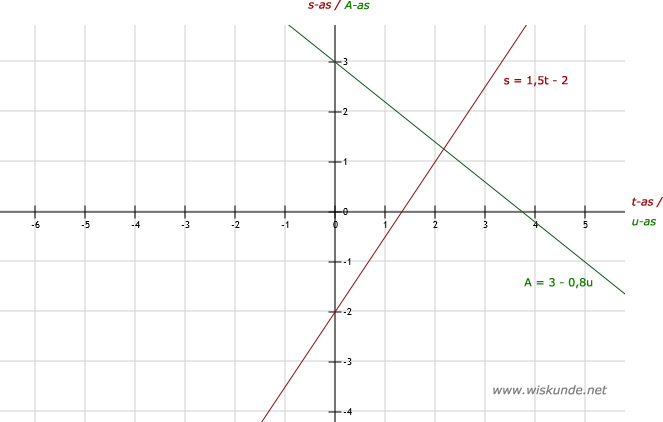
7.
b. (groen)
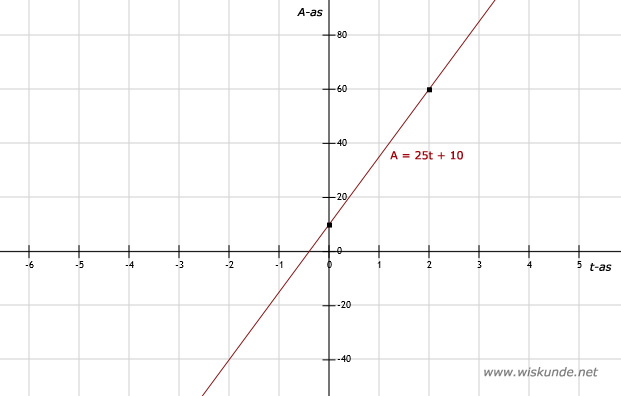
8.
b. Zie afbeelding
9.
b. B = 200 + 15 ⋅ 4,5 = 200 + 67,50 = 267,50 euro
c. B = 200 + 15 ⋅ 0 = 200 + 0 = 200 euro
d. 200 is een vast basisbedrag en 15 is de variabele prijs per 1000 views.
10.
a. Er bestaan geen negatieve kwartieren.
b. Zie afbeelding
c. Zie afbeelding
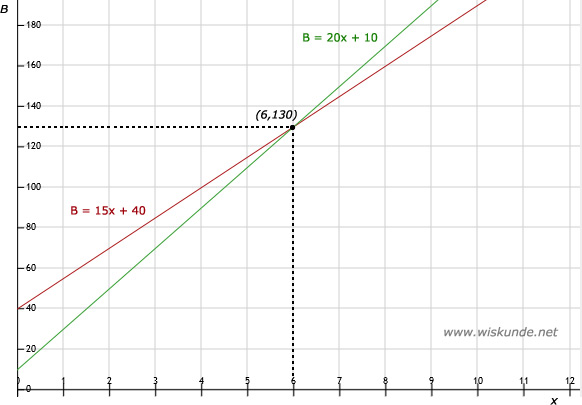
d. Snijpunt is (6,130)
e. De bedrijven zijn even duur bij 6 kwartier werken. Je betaalt dan bij beide 130,- euro.
Tip:
1500 m = 1,5 km
De tabel bij b: vormt de coördinaten van punten (x,y) die op een rechte lijn liggen.
a. 1500 m = 1,5 km
De tabel bij b: vormt de coördinaten van punten (x,y) die op een rechte lijn liggen.
V = 3 + 0,5 ⋅ 6 = 3 + 3 = 6. Dus 6 euro;
V = 3 + 0,5 ⋅ 1,5 = 3 + 0,75 = 3,75. Dus 3,75 euro;
b.
| x | 0 | 2 | 4 | 6 | 8 | 10 |
| V | 3 | 4 | 5 | 6 | 7 | 8 |
De punten op de grafiek zijn (zie tabel): (0,3), (2,4), (4,5), (6,6), (8,7) en (10,8).
d.
Prijs per kilometer is 0,5. Dus 50 eurocent.

2.
Tip:
Kies in de tabel altijd x = 0. Dit rekent altijd makkelijk.
a. Kies in de tabel altijd x = 0. Dit rekent altijd makkelijk.
| x | 0 | 4 |
| y | 1 | 3 |
b.
| x | 0 | 4 |
| y | 4 | -4 |

3.
Zie afbeelding

4.
Tip:
Kies 2 punten per lijn en teken dan de lijn.
Zie afbeelding
Kies 2 punten per lijn en teken dan de lijn.

5.
Tip:
Bij x = 0 heb je het snijpunt met de y-as.
a. Zie afbeeldingBij x = 0 heb je het snijpunt met de y-as.
b. Het snijpunt van deze 2 lijnen is: (2,-1)

6.
Tip:
Het is handig om 2 punten te kiezen voor een lijn die beide wel roosterpunten zijn.
In deze opgave hebben we een t-as en een B-as i.p.v. een x-as en y-as. Maar het komt op hetzelfde neer.
a. Het is handig om 2 punten te kiezen voor een lijn die beide wel roosterpunten zijn.
In deze opgave hebben we een t-as en een B-as i.p.v. een x-as en y-as. Maar het komt op hetzelfde neer.
| t | 0 | 5 |
| B | 2 | 5 |
b. Bij t = 2 krijg je als B-waarde 3,2. Dat tekent lastig in een assenstelsel want het is geen exact roosterpunt.
Nog een goede waarde is bij t = 10 of t = -5.
c. Zie afbeelding

7.
Tip:
Ik heb ze nu even in 1 plaatje gedaan.
a. (rood)Ik heb ze nu even in 1 plaatje gedaan.
| t | 0 | 4 |
| s | -2 | 4 |
b. (groen)
| u | 0 | 5 |
| A | 3 | -1 |

8.
Tip:
Een assenstelsel hoeft niet altijd in stappen van 1 te zijn. Kan ook 10 of 20 zijn.
a. Een assenstelsel hoeft niet altijd in stappen van 1 te zijn. Kan ook 10 of 20 zijn.
| t | 0 | 2 |
| A | 10 | 60 |
b. Zie afbeelding

9.
Tip:
v is in duizendtallen. Dus bij 6000 bezoekers is v gelijk aan 6.
a. Te betalen: B = 200 + 15 ⋅ 6 = 200 + 90 = 290 eurov is in duizendtallen. Dus bij 6000 bezoekers is v gelijk aan 6.
b. B = 200 + 15 ⋅ 4,5 = 200 + 67,50 = 267,50 euro
c. B = 200 + 15 ⋅ 0 = 200 + 0 = 200 euro
d. 200 is een vast basisbedrag en 15 is de variabele prijs per 1000 views.
10.
a. Er bestaan geen negatieve kwartieren.
b. Zie afbeelding
c. Zie afbeelding
d. Snijpunt is (6,130)
e. De bedrijven zijn even duur bij 6 kwartier werken. Je betaalt dan bij beide 130,- euro.

11.
b. y = -2x + 7
12.
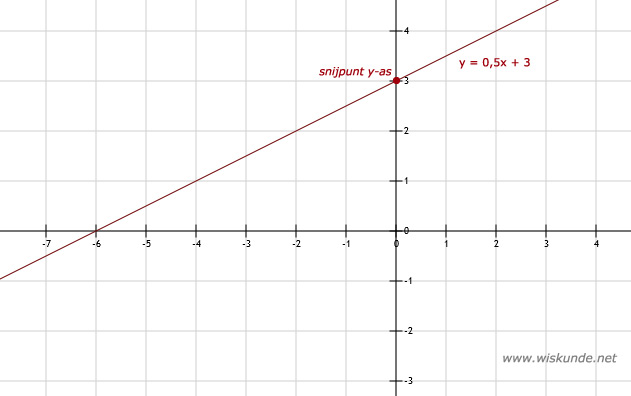
b. De grafiek snijdt de y-as in (0,3).
c. 3
d. Snijdt de y-as in (0,-8).
13.
a. a = -0,3 b = 2,6
b. a = 5 b = -1,4
c. a = 1 b = 8
d. a = -1 b = 1
e. a = 1 b = 0
f. a = -4 b = 0
g. a = 0 b = 2
h. a = 2 b = 3
i. a = -1 b = -9
14.
Snijden in de y-as: y = 2x + 2 en y = 0,5x + 2.
Dat zie je omdat ze gelijke b-waarde hebben (y = ax + b). De waarde van b is dus 2.
b.
Evenwijdig zijn: y = 0,5x - 4 en y = 0,5x + 2.
Dat zie je omdat ze gelijke a-waarde hebben (y = ax + b). De waarde van a is dus 0,5.
15.
y = 5x + 7 en y = 5x + 3 (i.v.m. 5)
y = -0,2x + 1 en y = -0,2x + 3 (i.v.m. -0,2)
b. Hetzelfde snijpunt met de y-as:
y = 5x + 7 en y = -4x + 7 (i.v.m. 7)
y = 4x + 3 en y = 5x + 3 en y = -0,2x + 3 (i.v.m. 3)
16.
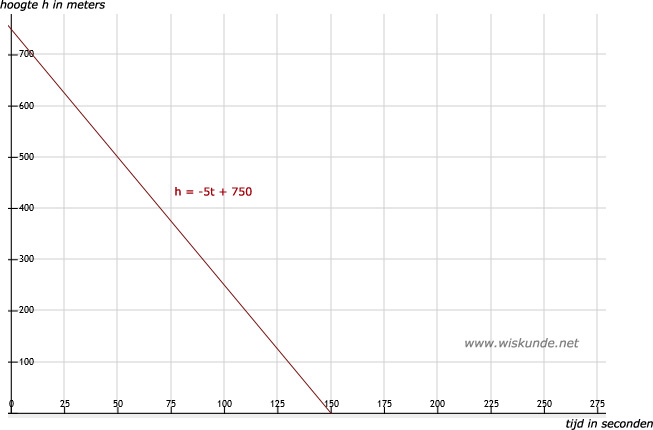
b. t = 50 invullen levert: h = -5 ⋅ 50 + 750 = 500 (meter)
t = 60 invullen levert: h = -5 ⋅ 60 + 750 = 450 (meter)
c. Zie afbeelding
d. Bij t = 150 geldt: h = -5 ⋅ 150 + 750 = -750 + 750 = 0 (meter)
Dus bij t = 150 (seconden) is de hoogte gelijk aan 0 (meter). Je krijgt dan het punt (150,0). Dit is het snijpunt met de x-as.
e. Per seconde daalt de parachute 5 meter.
Tip:
De basisvorm van een formule is: y = ax + b.
a. y = 15x + 20De basisvorm van een formule is: y = ax + b.
b. y = -2x + 7
12.
Tip:
Bij y = ax + b is het snijpunt met de y-as: (0,b).
Vul voor x maar 0 in dan zie je dat de y-waarde gelijk is aan b.
a. Bij y = ax + b is het snijpunt met de y-as: (0,b).
Vul voor x maar 0 in dan zie je dat de y-waarde gelijk is aan b.
| x | 0 | 2 |
| y | 3 | 4 |
b. De grafiek snijdt de y-as in (0,3).
c. 3
d. Snijdt de y-as in (0,-8).

13.
a. a = -0,3 b = 2,6
b. a = 5 b = -1,4
c. a = 1 b = 8
d. a = -1 b = 1
e. a = 1 b = 0
f. a = -4 b = 0
g. a = 0 b = 2
h. a = 2 b = 3
i. a = -1 b = -9
14.
Tip:
Grafieken die dezelfde a-waarde hebben (y = ax + b) zijn evenwijdig. Ze hebben dan gelijke richtingscoefficiënt.
Grafieken die dezelfde b-waarde hebben (y = ax + b) snijden elkaar in de y-as in punt (0,b).
a.Grafieken die dezelfde a-waarde hebben (y = ax + b) zijn evenwijdig. Ze hebben dan gelijke richtingscoefficiënt.
Grafieken die dezelfde b-waarde hebben (y = ax + b) snijden elkaar in de y-as in punt (0,b).
Snijden in de y-as: y = 2x + 2 en y = 0,5x + 2.
Dat zie je omdat ze gelijke b-waarde hebben (y = ax + b). De waarde van b is dus 2.
b.
Evenwijdig zijn: y = 0,5x - 4 en y = 0,5x + 2.
Dat zie je omdat ze gelijke a-waarde hebben (y = ax + b). De waarde van a is dus 0,5.
15.
Tip:
Het getal voor de x noemen we ook wel de richtingscoefficiënt.
a. Evenwijdig zijn:Het getal voor de x noemen we ook wel de richtingscoefficiënt.
y = 5x + 7 en y = 5x + 3 (i.v.m. 5)
y = -0,2x + 1 en y = -0,2x + 3 (i.v.m. -0,2)
b. Hetzelfde snijpunt met de y-as:
y = 5x + 7 en y = -4x + 7 (i.v.m. 7)
y = 4x + 3 en y = 5x + 3 en y = -0,2x + 3 (i.v.m. 3)
16.
Tip:
De grafiek heeft geen negatieve assen. Want negatieve seconden en negatieve hoogte bestaan niet.
a. t = 0 invullen levert: h = -5 ⋅ 0 + 750 = 750 (meter)De grafiek heeft geen negatieve assen. Want negatieve seconden en negatieve hoogte bestaan niet.
b. t = 50 invullen levert: h = -5 ⋅ 50 + 750 = 500 (meter)
t = 60 invullen levert: h = -5 ⋅ 60 + 750 = 450 (meter)
c. Zie afbeelding
d. Bij t = 150 geldt: h = -5 ⋅ 150 + 750 = -750 + 750 = 0 (meter)
Dus bij t = 150 (seconden) is de hoogte gelijk aan 0 (meter). Je krijgt dan het punt (150,0). Dit is het snijpunt met de x-as.
e. Per seconde daalt de parachute 5 meter.

Andere paragrafen:
5.1. Lineaire formules (1 t/m 16)
5.2. De richtingscoŽfficient van een lijn (17 t/m 26)
5.3. De formule van een lijn opstellen (27 t/m 33)
5.4. De balansmethode (34 t/m 52)
5.5. Vergelijkingen oplossen (53 t/m 69)
5.1. Lineaire formules (1 t/m 16)
5.2. De richtingscoŽfficient van een lijn (17 t/m 26)
5.3. De formule van een lijn opstellen (27 t/m 33)
5.4. De balansmethode (34 t/m 52)
5.5. Vergelijkingen oplossen (53 t/m 69)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


