TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.1 Opgaven VMBO 4 KGT
Boek: Getal & Ruimte - Meetkunde 1 VMBO 4 (deel 2) opgaven 1 t/m 83, 2011
1.
Kijkhoek rechteroog is ongeveer 157º
2.
Dat is het gebied wat het rode en groene gebied gemeen hebben (overlap). Dat is een hoek van ongeveer 125º.
3.
Het totale gezichtsveld is ongeveer 190º.
4.
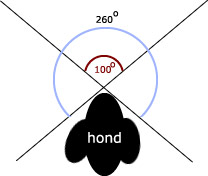
Teken een lijn van ieder oog langs de neus. De overlap is ongeveer 100º en het totale gezichtsveld is 260º.
5.
-
6.
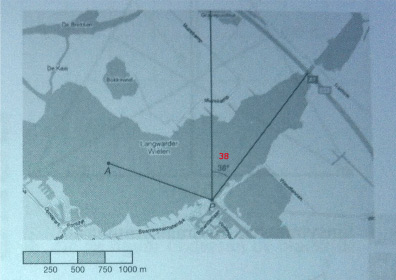
De koers die hij moet varen is: 38º
7.
Afstand van P tot de A7 is 1600 meter
8.
Zie afbeelding
9.
Zie afbeelding bij opgave 8.
10.
Minimaal zwemmen vanaf de boot naar de kant is 450 meter.
Kijkhoek rechteroog is ongeveer 157º
2.
Dat is het gebied wat het rode en groene gebied gemeen hebben (overlap). Dat is een hoek van ongeveer 125º.
3.
Het totale gezichtsveld is ongeveer 190º.
4.
Teken een lijn van ieder oog langs de neus. De overlap is ongeveer 100º en het totale gezichtsveld is 260º.
5.
-

6.
De koers die hij moet varen is: 38º
7.
Afstand van P tot de A7 is 1600 meter
8.
Zie afbeelding

9.
Zie afbeelding bij opgave 8.
10.
Minimaal zwemmen vanaf de boot naar de kant is 450 meter.
11.
Zie afbeelding
12.
Zie afbeelding bij opgave 11. Rechtsonder zie je een paarse cirkel. Daarop vind je meteen een trapezium.
13.
14.
Hoek AGB = 180º - 55º - 61º = 64º
Hoek BEF = 360º - 90º - 50º - 160º = 60º
Hoek CDE = 70º, gelijkbenige driehoek zijn de basishoeken even groot, dus 140º/2
15.
We herkennen daarin een vlieger.
16.
Begin met ∠E12 = 180º - 34º - 90º = 56º
∠E1 = ∠E2 = 28º
∠E3 = 34º
∠B1 = 118º
∠B2 = 62º
∠D1 = 12º
∠F2 = 102º
∠D2 = 44º
17.
Gebruik je passer. Zie afbeelding.
18.
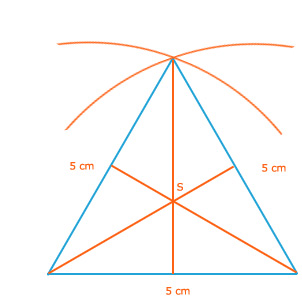
Een gelijkzijdige driehoek is lijn symmetrisch met 3 symmetrie-assen. Tevens is deze punt symmetrisch in punt S. Punt S noemen we ook wel het draaipunt van de symmetrie.
19.
Zie afbeelding.
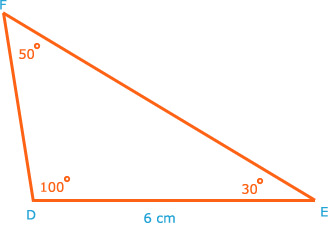
20.
Zet P als hoekpunt linksboven boven de 2. En zet Q als hoekpunt boven de 2,5. Zet R rechts als hoekpunt boven 2,5.
tan∠P1 = 1/6. Dus de hoek is 9º
sin∠Q1 = 1/8. Dus de hoek is 7º
sin∠R1 = 1/3. Dus de hoek is 19º
Dus de hoeken horende bij A en C zijn goed.
Zie afbeelding

12.
Zie afbeelding bij opgave 11. Rechtsonder zie je een paarse cirkel. Daarop vind je meteen een trapezium.
13.
| twee zijden even lang | diagonalen even lang | twee hoeken even groot | evenwijdige zijden | |
| vierkant | ja | ja | ja | ja |
| ruit | ja | nee | ja | ja |
| vlieger | ja | nee | ja | nee |
| parallellogram | ja | nee | ja | ja |
14.
Hoek AGB = 180º - 55º - 61º = 64º
Hoek BEF = 360º - 90º - 50º - 160º = 60º
Hoek CDE = 70º, gelijkbenige driehoek zijn de basishoeken even groot, dus 140º/2
15.
We herkennen daarin een vlieger.
16.
Begin met ∠E12 = 180º - 34º - 90º = 56º
∠E1 = ∠E2 = 28º
∠E3 = 34º
∠B1 = 118º
∠B2 = 62º
∠D1 = 12º
∠F2 = 102º
∠D2 = 44º
17.
Gebruik je passer. Zie afbeelding.

18.
Een gelijkzijdige driehoek is lijn symmetrisch met 3 symmetrie-assen. Tevens is deze punt symmetrisch in punt S. Punt S noemen we ook wel het draaipunt van de symmetrie.
19.
Zie afbeelding.

20.
Zet P als hoekpunt linksboven boven de 2. En zet Q als hoekpunt boven de 2,5. Zet R rechts als hoekpunt boven 2,5.
tan∠P1 = 1/6. Dus de hoek is 9º
sin∠Q1 = 1/8. Dus de hoek is 7º
sin∠R1 = 1/3. Dus de hoek is 19º
Dus de hoeken horende bij A en C zijn goed.
21.
sin 75º = hoogte meisje / 100
Hoogte tot meisje = 100 x sin 75º = 96,59 meter Hoogte vlieger = 96,59 + 1,05 = 97,64 meter
22.
Afstand = 1,10 / tan 7º ≈ 8,96 meter
23.
Hoogte huis = √44 ≈ 6,63 meter
24.
Hellingspercentage van het grasdak: 6,63 / 10 x 100% ≈ 66%
25.
AB = √40 ≈ 6,3 cm
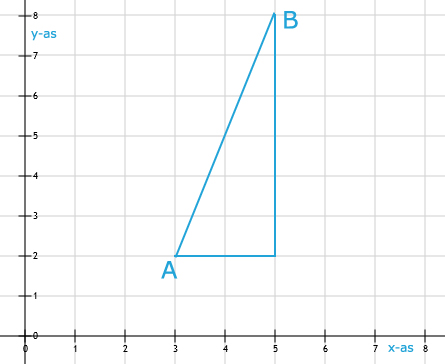
26.
De schaal heeft geen rechte hoek want want 441 + 625 is niet gelijk aan 1089. Want 212 + 252 ≠ 1089
27.
Hoogte boom = 6,16 meter
Bedenk dat de vergrotingsfactor = 3,25 : 0,95 = 3,42, dan 1,80 x 3,42 = 6,16
28.
Tan(zonnehoek) = 1,80 / 0,95
Zonnehoek = tan-1 (1,80 / 0,95) = 62º
29.
Oppervlakte 1e figuur = 2,4 x 4,2 ≈ 10 cm2
Oppervlakte 2e figuur = ½ x 7 x 2,3 ≈ 8 cm2
30.
Oppervlakte hartvormige vijver is 16,1 m2, namelijk een vierkant van 3x3 + 2 halve cirkels
sin 75º = hoogte meisje / 100
Hoogte tot meisje = 100 x sin 75º = 96,59 meter Hoogte vlieger = 96,59 + 1,05 = 97,64 meter
22.
Afstand = 1,10 / tan 7º ≈ 8,96 meter
23.
Hoogte huis = √44 ≈ 6,63 meter
24.
Hellingspercentage van het grasdak: 6,63 / 10 x 100% ≈ 66%
25.
AB = √40 ≈ 6,3 cm

26.
De schaal heeft geen rechte hoek want want 441 + 625 is niet gelijk aan 1089. Want 212 + 252 ≠ 1089
27.
Hoogte boom = 6,16 meter
Bedenk dat de vergrotingsfactor = 3,25 : 0,95 = 3,42, dan 1,80 x 3,42 = 6,16
28.
Tan(zonnehoek) = 1,80 / 0,95
Zonnehoek = tan-1 (1,80 / 0,95) = 62º
29.
Oppervlakte 1e figuur = 2,4 x 4,2 ≈ 10 cm2
Oppervlakte 2e figuur = ½ x 7 x 2,3 ≈ 8 cm2
30.
Oppervlakte hartvormige vijver is 16,1 m2, namelijk een vierkant van 3x3 + 2 halve cirkels
31.
Omtrek hartvormige vijver is 15,4 meter, namelijk 2x zijde vierkant + 2 halve cirkelbogen
32.
Omtrek van de gele figuur: Omtr. = 18,02 meter
Oppervlakte van de gele figuur: Opp. = 19,5 m2
33.
Omtrek van de rode figuur: Omtr. = 16,8 meter
Oppervlakte van de rode figuur: Opp. = 20,2 m2
34.
Vergrotingsfactor (f) is 450:29 ≈15,5
Oppervlakte muurschildering = f2 x 625 = 15,52 x 625 = 150156 cm2
Dat is ≈ 15m2
35.
Vergrotingsfactor = √(1,6/1,2) ≈ 1,15
36.
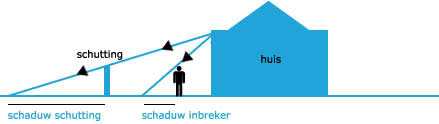
Aangezien de schaduw van de schutting ten oosten ligt, staat dus de zon in het westen.
37.
tan(zonnehoek) = 2 / 2,4
Dus de zonnehoek ≈ 40º
38.
Zie afbeelding

39.
Zie afbeelding opgave 38
40.
Zie afbeelding
Omtrek hartvormige vijver is 15,4 meter, namelijk 2x zijde vierkant + 2 halve cirkelbogen
32.
Omtrek van de gele figuur: Omtr. = 18,02 meter
Oppervlakte van de gele figuur: Opp. = 19,5 m2
33.
Omtrek van de rode figuur: Omtr. = 16,8 meter
Oppervlakte van de rode figuur: Opp. = 20,2 m2
34.
Vergrotingsfactor (f) is 450:29 ≈15,5
Oppervlakte muurschildering = f2 x 625 = 15,52 x 625 = 150156 cm2
Dat is ≈ 15m2
35.
Vergrotingsfactor = √(1,6/1,2) ≈ 1,15
36.
Aangezien de schaduw van de schutting ten oosten ligt, staat dus de zon in het westen.
37.
tan(zonnehoek) = 2 / 2,4
Dus de zonnehoek ≈ 40º
38.
Zie afbeelding

39.
Zie afbeelding opgave 38
40.
Zie afbeelding

41.
Vera kijkt naar het noorden omdat om 12:00 de zon in het zuiden staat. De zon komt op in het oosten.
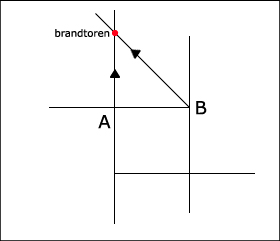
42.
Zie dat de brandtoren ongeveer 4,4 cm hoog is. De persoon naast de toren is ca. 0,2 cm. Dat is een factor 22.
Een mens is gemiddeld 1,8 m, dus de toren is ca. 1,8 x 22 = 40 meter
43.
Ze heeft een koers gelopen van ca. 47º.
44.
Koers van B naar de brandtoren is ca. 315º.
45.
De schaarlengte bevat 4 hele en 2 halve rode ruiten. Dus samen 5 rode ruiten. Dan 70 : 5 levert 14 cm voor AC.
46.
Schaal 1:2 d.w.z 1 cm op tekening (1 hokje) is 2 cm in het echt.
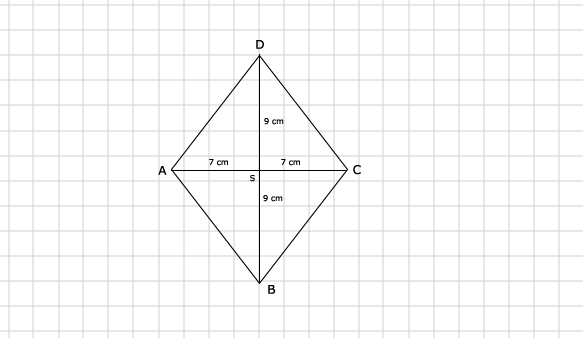
47.
In driehoek ASD = tan∠A1 = 9/7 ≈ 52º
∠A = ∠A1 + ∠A2
∠A = 104º
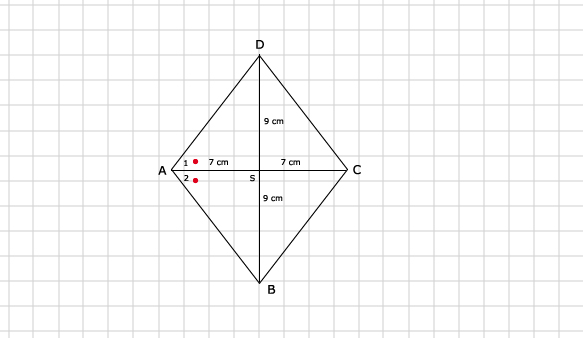
48.
BE = 2 x √130 ≈ 22,8 cm
49.
De schaarlengte hoort bij een breedte van 5 rode ruiten. Dus bij 10 halve rode "diagonalen".
Dan: cos 13º = x / √130 => x = 11,1 cm. Schaarlengte is 10 maal x en dat levert: 111 cm.
50.
Zie afbeelding
Vera kijkt naar het noorden omdat om 12:00 de zon in het zuiden staat. De zon komt op in het oosten.

42.
Zie dat de brandtoren ongeveer 4,4 cm hoog is. De persoon naast de toren is ca. 0,2 cm. Dat is een factor 22.
Een mens is gemiddeld 1,8 m, dus de toren is ca. 1,8 x 22 = 40 meter
43.
Ze heeft een koers gelopen van ca. 47º.
44.
Koers van B naar de brandtoren is ca. 315º.
45.
De schaarlengte bevat 4 hele en 2 halve rode ruiten. Dus samen 5 rode ruiten. Dan 70 : 5 levert 14 cm voor AC.
46.
Schaal 1:2 d.w.z 1 cm op tekening (1 hokje) is 2 cm in het echt.

47.
In driehoek ASD = tan∠A1 = 9/7 ≈ 52º
∠A = ∠A1 + ∠A2
∠A = 104º

48.
BE = 2 x √130 ≈ 22,8 cm
49.
De schaarlengte hoort bij een breedte van 5 rode ruiten. Dus bij 10 halve rode "diagonalen".
Dan: cos 13º = x / √130 => x = 11,1 cm. Schaarlengte is 10 maal x en dat levert: 111 cm.
50.
Zie afbeelding

51.
Niet verlicht op de tafel is: 8 036,5 cm2
52.
-
53.
Lengte touw is 88,2 cm
54.
A is lijnsymmetrisch met 1 symmetrieas
B is lijnsymmetrisch met 2 symmetrieassen
C is lijnsymmetrisch met 4 symmetrieassen
E is lijnsymmetrisch met oneindig veel symmetrieassen
F is lijnsymmetrisch met 3 symmetrieassen
G is lijnsymmetrisch met 8 symmetrieassen
H is lijnsymmetrisch met 2 symmetrieassen
I is lijnsymmetrisch met 4 symmetrieassen
55.
B, met kleinste draaihoek 180º
C, met kleinste draaihoek 90º
D, met kleinste draaihoek 180º
E
F, met kleinste draaihoek 120º
G, met kleinste draaihoek 45º
H, met kleinste draaihoek 180º
I, met kleinste draaihoek 90º
56.
Maten van de tegel: 45,6 cm
57.
Een segment = 360º : 12 = 30º
Driehoek ABM is gelijkbenig, dus de basishoeken zijn gelijk.
∠A + ∠B = 180º - 30º = 150º
Dus ∠A is de 150/2 => 75º
Hoek B is ook 75º, dus hieruit volgt dat ∠B12 = 150º
58.
∠EMI = 120º, namelijk 4 segmenten van 30º levert 120º.
59.
Oppervlakte van de twaalfhoek is 107,88 cm2.
60.
De twaalfhoek heeft 12 symmetrieassen.
Niet verlicht op de tafel is: 8 036,5 cm2
52.
-
53.
Lengte touw is 88,2 cm
54.
A is lijnsymmetrisch met 1 symmetrieas
B is lijnsymmetrisch met 2 symmetrieassen
C is lijnsymmetrisch met 4 symmetrieassen
E is lijnsymmetrisch met oneindig veel symmetrieassen
F is lijnsymmetrisch met 3 symmetrieassen
G is lijnsymmetrisch met 8 symmetrieassen
H is lijnsymmetrisch met 2 symmetrieassen
I is lijnsymmetrisch met 4 symmetrieassen
55.
B, met kleinste draaihoek 180º
C, met kleinste draaihoek 90º
D, met kleinste draaihoek 180º
E
F, met kleinste draaihoek 120º
G, met kleinste draaihoek 45º
H, met kleinste draaihoek 180º
I, met kleinste draaihoek 90º
56.
Maten van de tegel: 45,6 cm
57.
Een segment = 360º : 12 = 30º
Driehoek ABM is gelijkbenig, dus de basishoeken zijn gelijk.
∠A + ∠B = 180º - 30º = 150º
Dus ∠A is de 150/2 => 75º
Hoek B is ook 75º, dus hieruit volgt dat ∠B12 = 150º
58.
∠EMI = 120º, namelijk 4 segmenten van 30º levert 120º.
59.
Oppervlakte van de twaalfhoek is 107,88 cm2.
60.
De twaalfhoek heeft 12 symmetrieassen.
61.
Kleinste draaihoek van de twaalfhoek is 360º / 12 = 30º.
62.
-
63.
Vergrotingsfactor is 2, want de straal is 2x zo groot geworden.
64.
Oppervlakte van de grote figuur is 22 x 107,88 = 431,52 cm2
65.
-
66.
Oppervlakte stukje weiland is 3 m2.
67.
Kleiner
68.
In driehoek BCD gebruiken we de Stelling van Pythagoras.
BD = √12,50 ≈ 3,536 m
DS is de helft, dus DS = 1,77 meter.
69.
In driehoek ABS gebruiken we de Stelling van Pythagoras.
AS = √12,68 ≈ 3,56 m
70.
Oppervlakte vlieger is 9,4 m2
Kleinste draaihoek van de twaalfhoek is 360º / 12 = 30º.
62.
-
63.
Vergrotingsfactor is 2, want de straal is 2x zo groot geworden.
64.
Oppervlakte van de grote figuur is 22 x 107,88 = 431,52 cm2
65.
-
66.
Oppervlakte stukje weiland is 3 m2.
67.
Kleiner
68.
In driehoek BCD gebruiken we de Stelling van Pythagoras.
BD = √12,50 ≈ 3,536 m
DS is de helft, dus DS = 1,77 meter.
69.
In driehoek ABS gebruiken we de Stelling van Pythagoras.
AS = √12,68 ≈ 3,56 m
70.
Oppervlakte vlieger is 9,4 m2
71.
De IJssel is 68,7 meter breed.
72.
73,1 meter
73.
-
74.
rijen 1,3,5,7,9,11 (stoel 3 t/m 10) en vanaf rijen 2,4,6,8,10 (stoel 2 t/m 10)
75.
-
76.
46 º
77.
( 7, 4, 4 )
78.
420
80.
Hellingshoek is 10º
81.
Op het bord moet staan: 18%
De IJssel is 68,7 meter breed.
72.
73,1 meter
73.
-
74.
rijen 1,3,5,7,9,11 (stoel 3 t/m 10) en vanaf rijen 2,4,6,8,10 (stoel 2 t/m 10)
75.
-
76.
46 º
77.
( 7, 4, 4 )
78.
420
80.
Hellingshoek is 10º
81.
Op het bord moet staan: 18%
82.
Hoek B1 en hoek B2 zijn overstaande hoeken.
Hoek E is even groot als hoek A
AC = 20
83.
LM = 12 cm
OL = 5,2 cm
LN = 4,8 cm
Hoek B1 en hoek B2 zijn overstaande hoeken.
Hoek E is even groot als hoek A
AC = 20
83.
LM = 12 cm
OL = 5,2 cm
LN = 4,8 cm
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


