TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 7.1 Opgaven VMBO 4 KGT
Boek: Getal & Ruimte - Verbanden VMBO 4 (deel 2) opgaven 1 t/m 147, 2011Onderwerpen die aanbod komen zijn:
- Formules opstellen
- Van formule naar tabel
- Van grafiek naar formule
- Somformule en verschilformule
- Parabolen
- Formules opstellen
- Van formule naar tabel
- Van grafiek naar formule
- Somformule en verschilformule
- Parabolen
1.
I = 75 + 124t
2.
De variabelen in de formule zijn de letters: I en t.
3.
De eenheden die horen bij de variabelen zijn als volgt:
Bij I hoort euro en bij t hoort weken.
4.
Vul voor t = 12 in levert: I = 75 + 124 x 12 = €1563,-
5.
Een kwartaal is 13 weken. Vul voor t = 13 in levert: I = 75 + 124 x 13 = €1687,-
6.
Er is sprake van een lineair verband.
7.
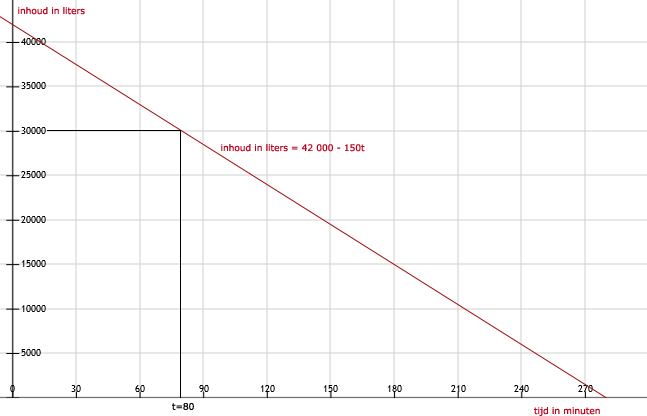
8.
Bij t = 80 zit er nog 30 000 liter in het zwembad.
Los op: 42 000 - 150t = 30 000
Levert: -150t = -12 000
Hieruit volgt: t = 80
9.
De variabelen in de formule zijn de letters: I en t.
10.
Zie afbeelding
I = 75 + 124t
2.
De variabelen in de formule zijn de letters: I en t.
3.
De eenheden die horen bij de variabelen zijn als volgt:
Bij I hoort euro en bij t hoort weken.
4.
Vul voor t = 12 in levert: I = 75 + 124 x 12 = €1563,-
5.
Een kwartaal is 13 weken. Vul voor t = 13 in levert: I = 75 + 124 x 13 = €1687,-
6.
Er is sprake van een lineair verband.
7.
| tijd | 0 | 60 | 80 | 120 | 180 | 270 |
| liters | 42000 | 33000 | 30000 | 24000 | 15000 | 1500 |

8.
Bij t = 80 zit er nog 30 000 liter in het zwembad.
Los op: 42 000 - 150t = 30 000
Levert: -150t = -12 000
Hieruit volgt: t = 80
9.
De variabelen in de formule zijn de letters: I en t.
10.
Zie afbeelding

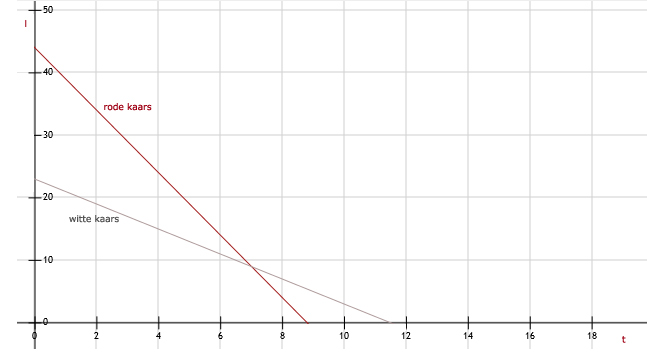
11.
Maximum van de rode kaars is 44 cm. Dit is het snijpunt met de y-as.
12.
Minimum van de witte kaars is 0 cm. Dit is het snijpunt met de x-as.
13.
Los op: 44 - 5t = 23 - 2t (snijpunt van de 2 lijnen)
3t = 21
t = 7
Dus bij t = 7 zijn beide kaarsen even lang.
14.
hoogte in meters = 600 - 10t
15.
Zie afbeelding
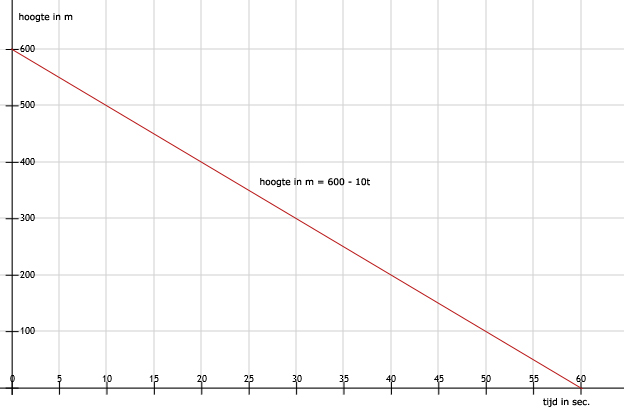
16.
Waar is de hoogte nul? Dat is bij 60 seconden.
17.
600 meter hoogte
18.
Stapgrootte = 5 en bij t = 0 hoort -1, dus de formule wordt:
Inhoud in liters = -1 + 5t
19.
Stapgrootte = 3 en bij t = 0 hoort 38, dus de formule wordt:
lengte in cm = 38 + 3t
20.
Stapgrootte = -50 en bij t = 0 hoort 250, dus de formule wordt:
inhoud in liters = 250 - 50t
Maximum van de rode kaars is 44 cm. Dit is het snijpunt met de y-as.
12.
Minimum van de witte kaars is 0 cm. Dit is het snijpunt met de x-as.
13.
Los op: 44 - 5t = 23 - 2t (snijpunt van de 2 lijnen)
3t = 21
t = 7
Dus bij t = 7 zijn beide kaarsen even lang.
14.
hoogte in meters = 600 - 10t
15.
Zie afbeelding

16.
Waar is de hoogte nul? Dat is bij 60 seconden.
17.
600 meter hoogte
18.
Stapgrootte = 5 en bij t = 0 hoort -1, dus de formule wordt:
Inhoud in liters = -1 + 5t
19.
Stapgrootte = 3 en bij t = 0 hoort 38, dus de formule wordt:
lengte in cm = 38 + 3t
20.
Stapgrootte = -50 en bij t = 0 hoort 250, dus de formule wordt:
inhoud in liters = 250 - 50t
21.
Stapgrootte = -50 : 2 = -25 en bij t = 0 hoort 100, dus de formule wordt:
inhoud in liters = 100 - 25t
22.
Stapgrootte = 100 : 10 = 10 en bij t = 0 hoort 0 euro, dus de formule wordt:
inkomsten in euro = 10t
23.
Stapgrootte = verticaal / horizontaal = 100 : 20 = 10 en bij t = 0 hoort 200 euro, dus de formule wordt:
inkomsten in euro = 200 + 5t
24.
Stapgrootte = verticaal / horizontaal = -1000 : 15 = -66,7 en bij t = 0 hoort 2500 liter, dus de formule wordt:
inhoud in liters = 2500 - 66,7t
25.
Maximum is 2500 liters
26.
Minimum is 500 liters
27.
Stapgrootte = verticaal / horizontaal = 1800 : 50 = 36 en bij t = 0 hoort 0 gram, dus de formule wordt:
G = 36t
28.
Stapgrootte = verticaal / horizontaal = 900 : 50 = 18 en bij t = 0 hoort 300 gram, dus de formule wordt:
G = 300 + 18t
29.
I C
II B
III A
IV D
V B
VI A
30.
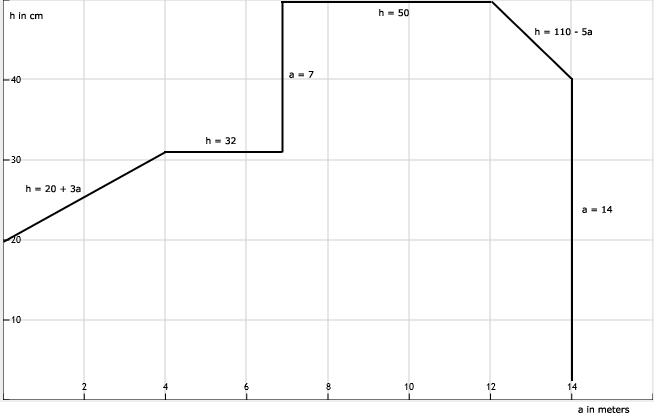
Zie afbeelding
Stapgrootte = -50 : 2 = -25 en bij t = 0 hoort 100, dus de formule wordt:
inhoud in liters = 100 - 25t
22.
Stapgrootte = 100 : 10 = 10 en bij t = 0 hoort 0 euro, dus de formule wordt:
inkomsten in euro = 10t
23.
Stapgrootte = verticaal / horizontaal = 100 : 20 = 10 en bij t = 0 hoort 200 euro, dus de formule wordt:
inkomsten in euro = 200 + 5t
24.
Stapgrootte = verticaal / horizontaal = -1000 : 15 = -66,7 en bij t = 0 hoort 2500 liter, dus de formule wordt:
inhoud in liters = 2500 - 66,7t
25.
Maximum is 2500 liters
26.
Minimum is 500 liters
27.
Stapgrootte = verticaal / horizontaal = 1800 : 50 = 36 en bij t = 0 hoort 0 gram, dus de formule wordt:
G = 36t
28.
Stapgrootte = verticaal / horizontaal = 900 : 50 = 18 en bij t = 0 hoort 300 gram, dus de formule wordt:
G = 300 + 18t
29.
I C
II B
III A
IV D
V B
VI A
30.
Zie afbeelding

31.
Voor grafiek zie afbeelding opgave 30.
32.
Voor grafiek zie afbeelding opgave 30.
33.
Voor grafiek zie afbeelding opgave 30.
34.
Voor grafiek zie afbeelding opgave 30.
35.
Voor grafiek zie afbeelding opgave 30.
36.
Voor grafiek zie afbeelding opgave 30.
37.
Zie afbeelding
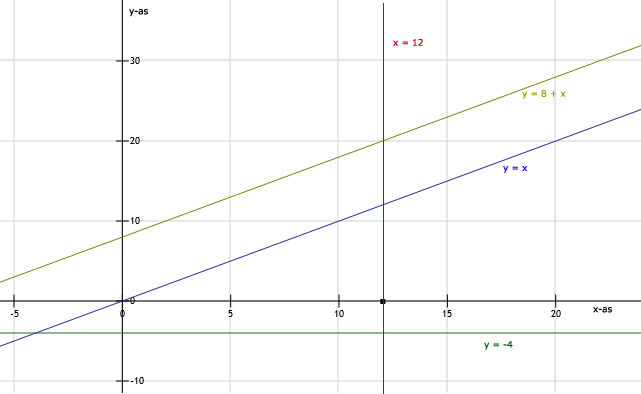
38.
Zie afbeelding opgave 37
39.
grafiek I is t = -10
grafiek II is G = 15
grafiek III is G = -5
grafiek IV is G = t
grafiek V is t = 15
40.
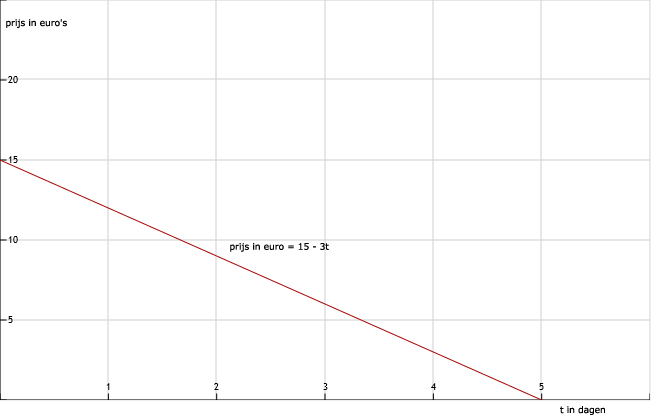
Verschilformule is: prijs in euro = 15 - 3t
Voor grafiek zie afbeelding opgave 30.
| a | 0 | 2 | 4 |
| h | 20 | 26 | 32 |
32.
Voor grafiek zie afbeelding opgave 30.
| a | 4 | 5 | 7 |
| h | 32 | 32 | 32 |
33.
Voor grafiek zie afbeelding opgave 30.
| a | 7 | 7 | 7 |
| h | 32 | 42 | 50 |
34.
Voor grafiek zie afbeelding opgave 30.
| a | 7 | 10 | 12 |
| h | 50 | 50 | 50 |
35.
Voor grafiek zie afbeelding opgave 30.
| a | 12 | 13 | 14 |
| h | 50 | 45 | 40 |
36.
Voor grafiek zie afbeelding opgave 30.
| a | 14 | 14 | 14 |
| h | 40 | 20 | 0 |
37.
Zie afbeelding

38.
Zie afbeelding opgave 37
39.
grafiek I is t = -10
grafiek II is G = 15
grafiek III is G = -5
grafiek IV is G = t
grafiek V is t = 15
40.
Verschilformule is: prijs in euro = 15 - 3t
41.
Zie afbeelding
42.
De verschilfunctie geeft aan hoeveel je meer voor hut B betaalt in relatie met hut A.
43.
Invullen t = 2 levert
Type A: 15 + 55 x 2 = 125
Type B: 30 + 52 x 2 = 134
Dus type A is goedkoper
44.
Invullen t = 6 levert
Type A: 15 + 55 x 6 = 345
Type B: 30 + 52 x 6 = 342
Dus type B is goedkoper
45.
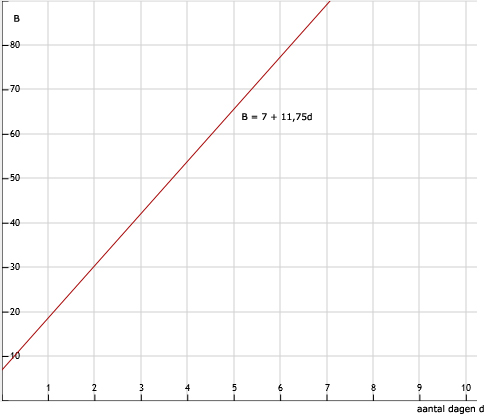
Somformule is: B = 7 + 11,75d
46.
Zie afbeelding
47.
Vergelijking wordt: 7 + 11,75d = 136,25
11,75d = 129,25
d = 11
Dus in totaal 11 dagen gehuurd.
48.
Formule Mark: B = 9 + 0,15k
Formule Sanne: B = 5 + 0,20k
49.
5 + 0,20k = 9 + 0,15k
0,20k = 4 + 0,15k
0,05k = 4
k = 80
50.
Als ze beiden 80 km rijden, betalen ze evenveel.
Zie afbeelding

42.
De verschilfunctie geeft aan hoeveel je meer voor hut B betaalt in relatie met hut A.
43.
Invullen t = 2 levert
Type A: 15 + 55 x 2 = 125
Type B: 30 + 52 x 2 = 134
Dus type A is goedkoper
44.
Invullen t = 6 levert
Type A: 15 + 55 x 6 = 345
Type B: 30 + 52 x 6 = 342
Dus type B is goedkoper
45.
Somformule is: B = 7 + 11,75d
46.
Zie afbeelding

47.
Vergelijking wordt: 7 + 11,75d = 136,25
11,75d = 129,25
d = 11
Dus in totaal 11 dagen gehuurd.
48.
Formule Mark: B = 9 + 0,15k
Formule Sanne: B = 5 + 0,20k
49.
5 + 0,20k = 9 + 0,15k
0,20k = 4 + 0,15k
0,05k = 4
k = 80
50.
Als ze beiden 80 km rijden, betalen ze evenveel.
51.
Vul k=85 in in de formules. Mark betaalt dan 21,75 en Sanne betaalt dan 22,00. Dus Mark betaalt het minst.
52.
(9 + 0,15k) - (5 + 0,20k) => B = 4 - 0,05k
53.
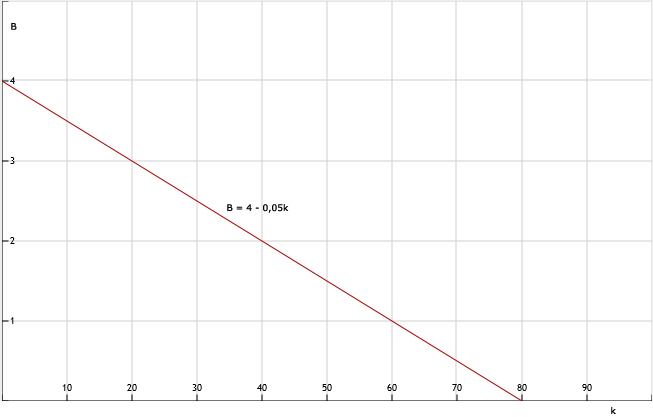
54.
Bij 80 km is er geen verschil.
55.
De antwoorden zijn gelijk.
56.
Stapgrootte = verticaal : horizontaal = 60 : 1000 = 0,06 en bij a = 0 hoort 4 euro, dus de formule wordt:
inkomsten in euro = 4 + 0,06a
57.
Stapgrootte = verticaal : horizontaal = 4 : 100 = 0,04 en bij a = 0 hoort 10 euro, dus de formule wordt:
inkomsten in euro = 10 + 0,04a
58.
Inkomsten Kenneth
59.
Zie afbeelding
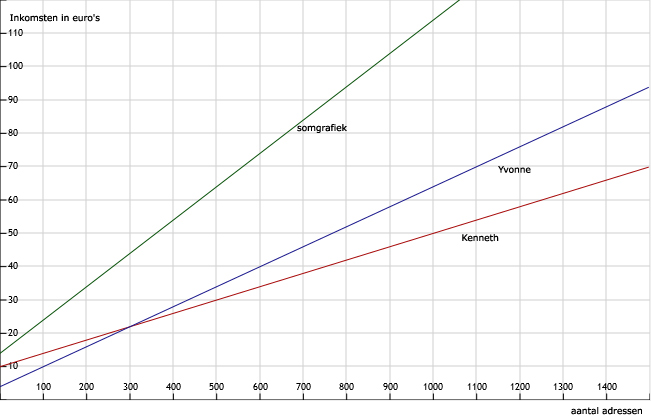
60.
Bij 300 adressen verdienen ze beiden evenveel (22 euro). Het snijpunt is dus (300,22).
Vul k=85 in in de formules. Mark betaalt dan 21,75 en Sanne betaalt dan 22,00. Dus Mark betaalt het minst.
52.
(9 + 0,15k) - (5 + 0,20k) => B = 4 - 0,05k
53.
| k | 0 | 20 | 40 | 60 | 80 | 100 |
| B | 4 | 3 | 2 | 1 | 0 | -1 |

54.
Bij 80 km is er geen verschil.
55.
De antwoorden zijn gelijk.
56.
Stapgrootte = verticaal : horizontaal = 60 : 1000 = 0,06 en bij a = 0 hoort 4 euro, dus de formule wordt:
inkomsten in euro = 4 + 0,06a
57.
Stapgrootte = verticaal : horizontaal = 4 : 100 = 0,04 en bij a = 0 hoort 10 euro, dus de formule wordt:
inkomsten in euro = 10 + 0,04a
58.
Inkomsten Kenneth
| aantal adressen | 100 | 200 | 300 | 400 | 1000 |
| inkomsten in euro's | 14 | 18 | 22 | 26 | 50 |
59.
Zie afbeelding

60.
Bij 300 adressen verdienen ze beiden evenveel (22 euro). Het snijpunt is dus (300,22).
61.
Somformule is (4 + 0,06a) + (10 + 0,04a):
inkomsten in euro = 14 + 0,1a
62.
Zie afbeelding opgave 59
63.
14 + 0,1a = 106,40
0,1a = 92,40
Oplossen geeft: a = 924
Dus dat waren 924 adressen op die dag.
64.
ja, kies bijvoorbeeld a = 0 en a = 10 en kijk of ze dezelfde uitkomsten geven.
65.
formule 2 en 4
66.
A = 0,007v2 + 0,28v + 2
67.
Zie afbeelding
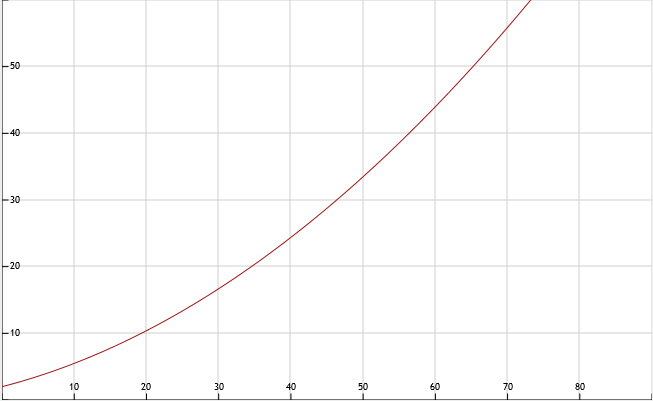
68.
a = 60 geeft afstand = 44, a = 61 geeft afstand 45,13. Dus Jamal rijdt tussen de 60 en 61 km/uur.
69.
De boog vormt een bergparabool.
70.
Teken in je werkboek de lijn m = 3.
Somformule is (4 + 0,06a) + (10 + 0,04a):
inkomsten in euro = 14 + 0,1a
62.
Zie afbeelding opgave 59
63.
14 + 0,1a = 106,40
0,1a = 92,40
Oplossen geeft: a = 924
Dus dat waren 924 adressen op die dag.
64.
ja, kies bijvoorbeeld a = 0 en a = 10 en kijk of ze dezelfde uitkomsten geven.
65.
formule 2 en 4
66.
A = 0,007v2 + 0,28v + 2
| v | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| A | 2 | 5,5 | 10,4 | 16,7 | 24,4 | 33,5 | 44 | 55,9 |
67.
Zie afbeelding

68.
a = 60 geeft afstand = 44, a = 61 geeft afstand 45,13. Dus Jamal rijdt tussen de 60 en 61 km/uur.
69.
De boog vormt een bergparabool.
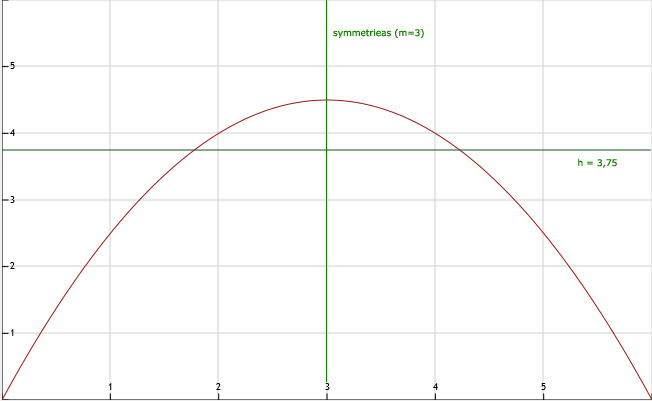
70.
Teken in je werkboek de lijn m = 3.

71.
Het maximum is de y-waarde van de top: 4,5
72.
73.
Formule III
74.
Zie afbeelding bij opgave 70.
75.
Bij a = 1,8 en a = 4,2 komen we redelijk in de buurt van h = 3,75. De breedte van de tunnel is dus ongeveer 4,2 - 1,8 = 2,4 meter.
Met inklemmen kom je bij a = 1,775
76.
Breedte tunnel - 2 x 5 cm levert: 2,40 - 0,10 = 2,30 meter.
77.
78.
Zie afbeelding
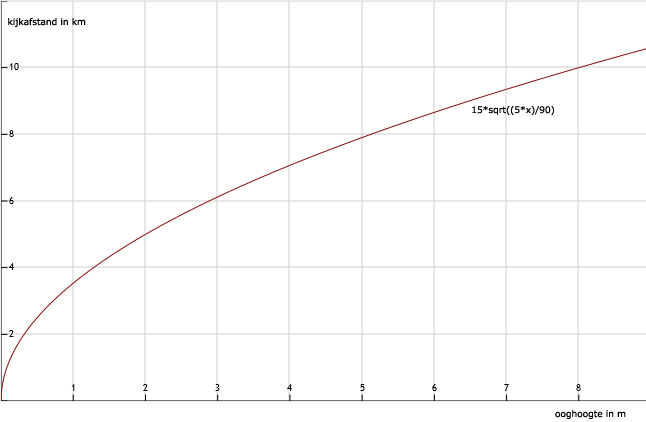
79.
Bij h = 11,5 is de kijkafstand 11,99 (dus bijna 12) km.
80.
Bedenk een verdieping is 3 meter. Dus Selma staat dan op de 3e verdieping (9 tot 12 meter).
Het maximum is de y-waarde van de top: 4,5
72.
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| h | 0 | 2,5 | 4 | 4,5 | 4 | 2,5 | 0 |
73.
Formule III
74.
Zie afbeelding bij opgave 70.
75.
Bij a = 1,8 en a = 4,2 komen we redelijk in de buurt van h = 3,75. De breedte van de tunnel is dus ongeveer 4,2 - 1,8 = 2,4 meter.
Met inklemmen kom je bij a = 1,775
76.
Breedte tunnel - 2 x 5 cm levert: 2,40 - 0,10 = 2,30 meter.
77.
| h | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| kijkafstand | 0 | 3,5 | 5 | 6,1 | 7,1 | 7,9 | 8,7 | 9,4 | 10 | 10,6 |
78.
Zie afbeelding

79.
Bij h = 11,5 is de kijkafstand 11,99 (dus bijna 12) km.
80.
Bedenk een verdieping is 3 meter. Dus Selma staat dan op de 3e verdieping (9 tot 12 meter).
81.
Zijde = 1,52 x √20 ≈ 6,8 cm.
82.
zijde = 1,52 x √(oppervlakte)
83.
Zijde is dus 24,32 cm. Omtrek is 3 x 24,32 = 72,96 cm.
84.
Oppervlakte van 1 zo'n driehoek is 150 : 6 = 25 cm2. Zijde is dus 7,6 cm. Omtrek is 6 x 7,6 = 45,6 cm.
85.
De oppervlakte is ongeveer 43,3 cm2. Je krijgt namelijk: 10 = 1,52 x √opp
Bij opp = 43,2 krijg je zijde = 9,9905
Bij opp = 43,3 krijg je zijde = 10,0020
86.
87.
Zie afbeelding
88.
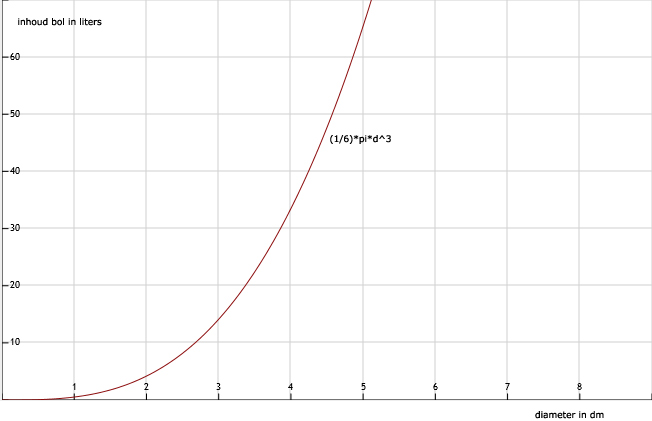
inhoud voetbal = 1/6 x π x 2,23 = 5,6 liter
89.
Diameter van de bol is 27 cm. Bij d = 2,6 krijg je 1/6 x π x 2,63 = 9,20 liter en bij d = 2,7 krijg je 1/6 x π x 2,73 = 10,30 liter. En 2,7 dm = 27 cm.
90.
Zijde = 1,52 x √20 ≈ 6,8 cm.
82.
zijde = 1,52 x √(oppervlakte)
| oppervlakte | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| zijde | 0 | 3,4 | 4,8 | 5,9 | 6,8 | 7,6 | 8,3 |
83.
Zijde is dus 24,32 cm. Omtrek is 3 x 24,32 = 72,96 cm.
84.
Oppervlakte van 1 zo'n driehoek is 150 : 6 = 25 cm2. Zijde is dus 7,6 cm. Omtrek is 6 x 7,6 = 45,6 cm.
85.
De oppervlakte is ongeveer 43,3 cm2. Je krijgt namelijk: 10 = 1,52 x √opp
Bij opp = 43,2 krijg je zijde = 9,9905
Bij opp = 43,3 krijg je zijde = 10,0020
86.
| d | 0 | 1 | 2 | 3 | 4 | 5 | 8 |
| inhoud bol | 0 | 0,52 | 4,19 | 14,14 | 33,51 | 65,45 | 268,08 |
87.
Zie afbeelding

88.
inhoud voetbal = 1/6 x π x 2,23 = 5,6 liter
89.
Diameter van de bol is 27 cm. Bij d = 2,6 krijg je 1/6 x π x 2,63 = 9,20 liter en bij d = 2,7 krijg je 1/6 x π x 2,73 = 10,30 liter. En 2,7 dm = 27 cm.
90.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| A | 0 | 25 | 32 | 27 | 16 | 5 | 0 |
91.
Zie afbeelding
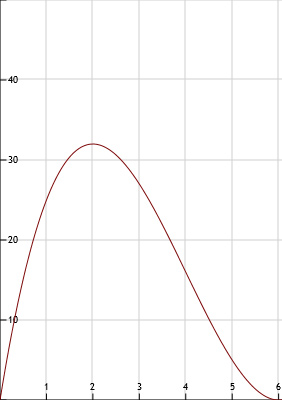
92.
Er staan maximaal 32 mensen te wachten, dat is rond 11:00.
93.
94.
Zie afbeelding
95.
De maximale winst is bij 2000 bezoekers. De winst is dan 30.000 euro. Dit is bij de top van de parabool.
96.
Verlies bij als aantal bezoekers minder is dan 268 en meer dan 3732 bezoekers.
97.
3095 bezoekers. Als a = 905 dan is de winst ongeveer 18.009,75 euro. En ook bij 4000 - 905 = 3095. De parabool is symmetrisch. De lijn y = 18000 snijdt de parabool in 2 punten.
98.
512 dm2
99.
Na 14 dagen. Bij t = 14 is de oppervlakte van de waterlelie 8192 dm2. Bij t = 13 is de oppervlakte nog 4096 dm2.
100.
t = 14 geeft oppervlakte 8192
t = 15 geeft oppervlakte 16384
Er komt dus 16384 - 8192 = 8192 dm2 bij.
Zie afbeelding

92.
Er staan maximaal 32 mensen te wachten, dat is rond 11:00.
93.
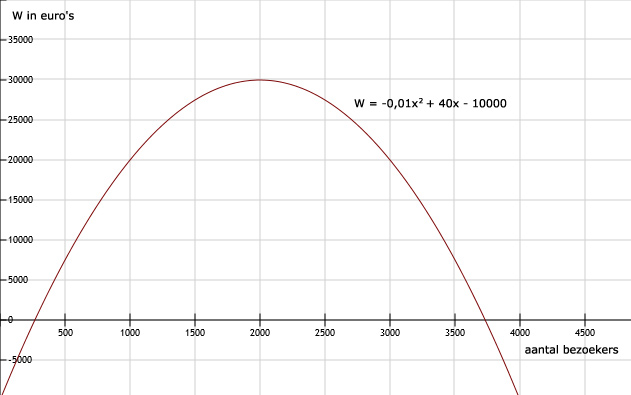
| a | 0 | 500 | 1000 | 2000 | 3000 | 4000 |
| W | -10000 | 7500 | 20000 | 30000 | 20000 | -10000 |
94.
Zie afbeelding

95.
De maximale winst is bij 2000 bezoekers. De winst is dan 30.000 euro. Dit is bij de top van de parabool.
96.
Verlies bij als aantal bezoekers minder is dan 268 en meer dan 3732 bezoekers.
97.
3095 bezoekers. Als a = 905 dan is de winst ongeveer 18.009,75 euro. En ook bij 4000 - 905 = 3095. De parabool is symmetrisch. De lijn y = 18000 snijdt de parabool in 2 punten.
98.
512 dm2
99.
Na 14 dagen. Bij t = 14 is de oppervlakte van de waterlelie 8192 dm2. Bij t = 13 is de oppervlakte nog 4096 dm2.
100.
t = 14 geeft oppervlakte 8192
t = 15 geeft oppervlakte 16384
Er komt dus 16384 - 8192 = 8192 dm2 bij.
101.
De dag van morgen is 2x de dag van vandaag. Dus als de vijver vandaag halfvol is, dan is deze morgen helemaal vol. Dus nog 1 dag. Dit kun je ook zien omdat de groeifactor 2 is.
102.
Groeifactor is ongeveer 1,1 want 440 / 400 is 1,1. Dat geldt ook bij de andere verhoudingen.
t = 0 levert 400
Formule wordt dus: aantal reigers = 400 x 1,1t
103.
Zie afbeelding
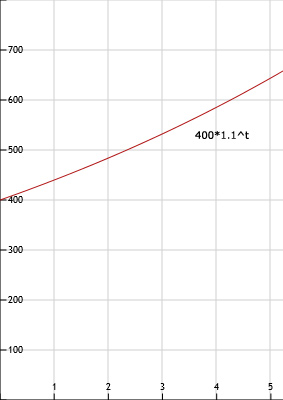
104.
Groeifactor is 1,098. Dat is gelijk aan 109,8%. Dus de toename is 9,8%.
105.
Invullen t = 3 levert: 3144 lepelaars in 2013.
106.
Bij t = 20 geeft A ≈ 15407 lepelaars. Dus in 2030 zijn het er al veel meer. Dus ergens in de loop van 2029 passeren we de 15000.
107.
Invullen t = 3 geeft: V = 9,2 x 0,9753 ≈ 8,5 liter in de ballon.
109.
Na 8 uur
110.
Tijdens de negende ademstoot klapt de ballon.
111.
20%
De dag van morgen is 2x de dag van vandaag. Dus als de vijver vandaag halfvol is, dan is deze morgen helemaal vol. Dus nog 1 dag. Dit kun je ook zien omdat de groeifactor 2 is.
102.
Groeifactor is ongeveer 1,1 want 440 / 400 is 1,1. Dat geldt ook bij de andere verhoudingen.
t = 0 levert 400
Formule wordt dus: aantal reigers = 400 x 1,1t
103.
Zie afbeelding

104.
Groeifactor is 1,098. Dat is gelijk aan 109,8%. Dus de toename is 9,8%.
105.
Invullen t = 3 levert: 3144 lepelaars in 2013.
106.
Bij t = 20 geeft A ≈ 15407 lepelaars. Dus in 2030 zijn het er al veel meer. Dus ergens in de loop van 2029 passeren we de 15000.
107.
Invullen t = 3 geeft: V = 9,2 x 0,9753 ≈ 8,5 liter in de ballon.
109.
Na 8 uur
110.
Tijdens de negende ademstoot klapt de ballon.
111.
20%
112.
De waarde van de fiets na 5 jaar is: €173,67.
113.
Halveringstijd is 4 jaar.
114.
Groeifactor is 1,028. Dus spaarbedrag = 350 x 1,028t
115.
Invullen t = 5 levert: € 401,82
116.
Bij t = 26 is het spaarbedrag € 717,61. Dus medio 2035 is het bedrag verdubbeld.
117.
Formule: 350 x 1,04t en t = 0 is 1 jan. 2010.
Bij t = 18 is het spaarbedrag € 709,04. Dus medio 2027 is het bedrag verdubbeld. Want op 1 jan. 2028 is het bedrag al meer dan verdubbeld.
118.
18 : 6 = 3 euro.
119.
V x B = 18 en B = 18 : V
120.
9 vriendinnen
121.
Zie afbeelding
De waarde van de fiets na 5 jaar is: €173,67.
113.
Halveringstijd is 4 jaar.
114.
Groeifactor is 1,028. Dus spaarbedrag = 350 x 1,028t
115.
Invullen t = 5 levert: € 401,82
116.
Bij t = 26 is het spaarbedrag € 717,61. Dus medio 2035 is het bedrag verdubbeld.
117.
Formule: 350 x 1,04t en t = 0 is 1 jan. 2010.
Bij t = 18 is het spaarbedrag € 709,04. Dus medio 2027 is het bedrag verdubbeld. Want op 1 jan. 2028 is het bedrag al meer dan verdubbeld.
118.
18 : 6 = 3 euro.
119.
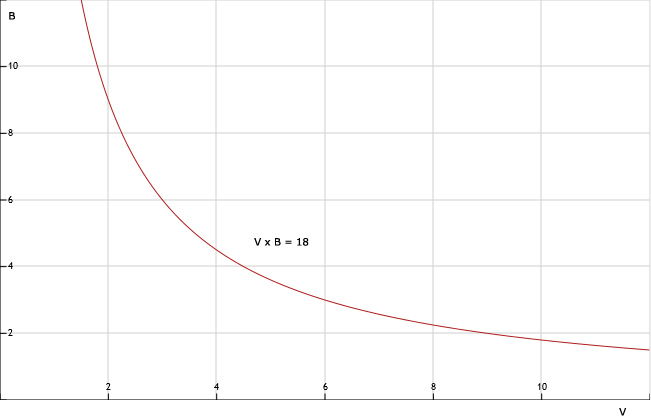
V x B = 18 en B = 18 : V
120.
9 vriendinnen
121.
Zie afbeelding

122.
36 km : 18 km/uur = 2 uur
123.
36 km : 24 km/uur = 1,5 uur
124.
kleiner
125.
Bij het verhaal hoort een omgekeerd evenredig verband.
126.
Formules: I en II en IV
127.
Zie afbeelding
128.
36 : 30 = 1,2 uur. Bedenk 0,1 uur = 6 minuten. Dus 0,2 uur is 12 minuten.
Dus 1,2 uur is 1 uur en 12 minuten.
129.
60 km/uur. Want in 36 minuten rijdt ze 36 km. In 1 minuut dus 1 km. In 60 minuten dus 60 km.
130.
131.
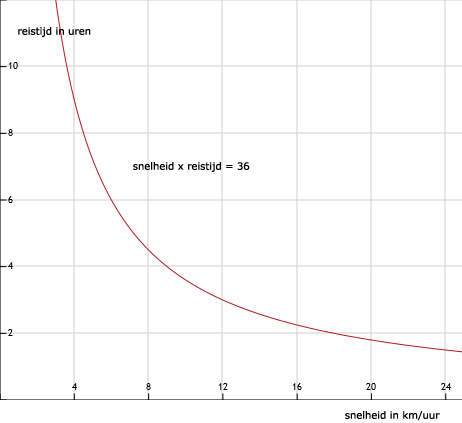
Zie afbeelding
36 km : 18 km/uur = 2 uur
123.
36 km : 24 km/uur = 1,5 uur
124.
kleiner
125.
Bij het verhaal hoort een omgekeerd evenredig verband.
126.
Formules: I en II en IV
127.
Zie afbeelding

128.
36 : 30 = 1,2 uur. Bedenk 0,1 uur = 6 minuten. Dus 0,2 uur is 12 minuten.
Dus 1,2 uur is 1 uur en 12 minuten.
129.
60 km/uur. Want in 36 minuten rijdt ze 36 km. In 1 minuut dus 1 km. In 60 minuten dus 60 km.
130.
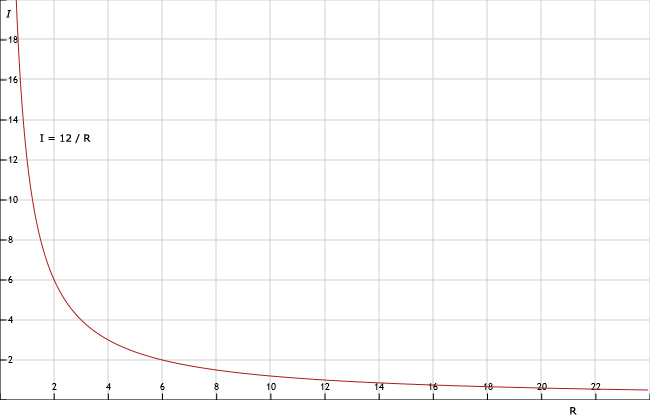
| R | 0,5 | 1 | 1,5 | 2 | 3 | 4 | 6 | 12 | 24 |
| I | 24 | 12 | 8 | 6 | 4 | 3 | 2 | 1 | 0,5 |
131.
Zie afbeelding

132.
Dan wordt I 10x zo klein.
133.
Als 6 = 12 / 2 dan geldt ook 2 = 12 / 6. Dus I = 12 / R is hetzelfde als R = 12 / I
134.
Het reuzenrad is 35 meter hoog.
135.
*
136.
*
137.
Na 100 seconden
138.
Het reuzenrad is dan 2 keer rond geweest en het minirad 5 keer.
139.
Annet is dan 130 meter hoog.
140.
17,5 meter
141.
De frequenties zijn 72 per uur en 180 per uur
Dan wordt I 10x zo klein.
133.
Als 6 = 12 / 2 dan geldt ook 2 = 12 / 6. Dus I = 12 / R is hetzelfde als R = 12 / I
134.
Het reuzenrad is 35 meter hoog.
135.
*
136.
*
137.
Na 100 seconden
138.
Het reuzenrad is dan 2 keer rond geweest en het minirad 5 keer.
139.
Annet is dan 130 meter hoog.
140.
17,5 meter
141.
De frequenties zijn 72 per uur en 180 per uur
142.
Het verschil is 10 cm.
143.
Je ziet 2 etmalen.
144.
Iets minder dan 12 uur.
145.
Het is hoogwater rond 09:00 uur en rond 21:00 uur.
146.
Evenwichtsstand is 0 cm.
147.
Amplitude is 150 cm.
Het verschil is 10 cm.
143.
Je ziet 2 etmalen.
144.
Iets minder dan 12 uur.
145.
Het is hoogwater rond 09:00 uur en rond 21:00 uur.
146.
Evenwichtsstand is 0 cm.
147.
Amplitude is 150 cm.
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


