TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 8.1 Opgaven VMBO 4 KGT
Boek: Getal & Ruimte - Meetkunde 2 VMBO 4 (deel 2) opgaven 1 t/m 70, 2011Onderwerpen die aanbod komen zijn:
- Ruimtefiguren tekenen
- Hoe teken ik een kubus en een balk?
- Evenwijdige, kruisende en snijdende lijnen
- Aanzichten maken en bekijken
- Een uitslag maken
- Doorsneden
- Pythagoras
- Hoogtelijnen
- Inhouden berekenen
- Ruimtefiguren tekenen
- Hoe teken ik een kubus en een balk?
- Evenwijdige, kruisende en snijdende lijnen
- Aanzichten maken en bekijken
- Een uitslag maken
- Doorsneden
- Pythagoras
- Hoogtelijnen
- Inhouden berekenen
1.
2.
3.
Zie afbeelding
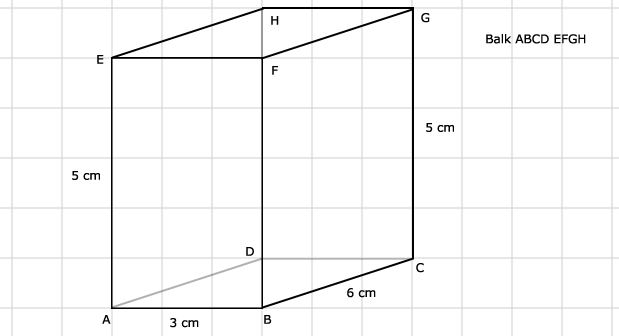
4.
Zie afbeelding
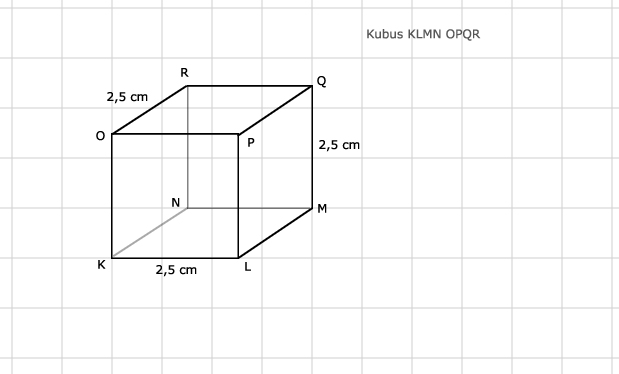
5.
De ribben die evenwijdig zijn met PQ zijn: OR, LM en KN.
6.
De ribben die PQ kruisen zijn: KO, KL, NR en MN.
7.
8.
De ribben PS, SW en RS.
9.
Zie afbeelding met de balk met diagonaalvlak PQVW.
De ribben die PW kruisen zijn: TU, RS, QR, UV, VR en QU
De diagonalen (rood) die PW kruisen zijn: TV, UR, SQ, SV en TQ
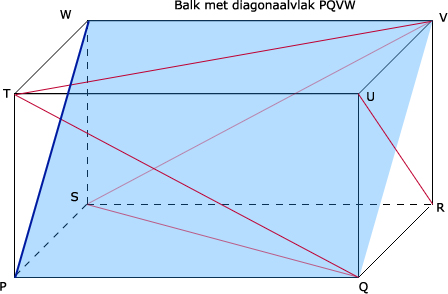
10.
Zie afbeelding
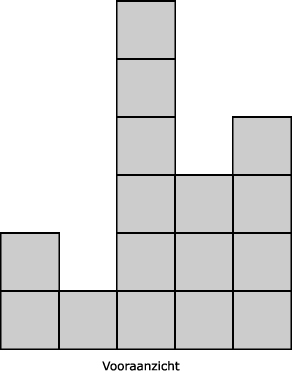
| grensvlak(ken) | kubus | balk | bol | kegel | prisma | piramide | cilinder |
| 1 gebogen | X | ||||||
| 6 platte | X | X | X | ||||
| 1 gebogen + 2 platte | X | ||||||
| 1 gebogen + 1 platte | X | ||||||
| 5 platte | X | X |
2.
| A | B | C | D | |
| Aantal grensvlakken | 5 | 6 | 5 | 6 |
| Aantal ribben | 8 | 12 | 9 | 12 |
| Aantal hoekpunten | 5 | 8 | 6 | 8 |
| Naam | Piramide | Balk | Prisma | Kubus |
3.
Zie afbeelding

4.
Zie afbeelding

5.
De ribben die evenwijdig zijn met PQ zijn: OR, LM en KN.
6.
De ribben die PQ kruisen zijn: KO, KL, NR en MN.
7.
| ribben | snijdend | evenwijdig | kruisend |
| AB en GJ | X | ||
| AD en IJ | X | ||
| BC en EH | X | ||
| HJ en DH | X |
8.
De ribben PS, SW en RS.
9.
Zie afbeelding met de balk met diagonaalvlak PQVW.
De ribben die PW kruisen zijn: TU, RS, QR, UV, VR en QU
De diagonalen (rood) die PW kruisen zijn: TV, UR, SQ, SV en TQ

10.
Zie afbeelding

11.
Zie afbeelding
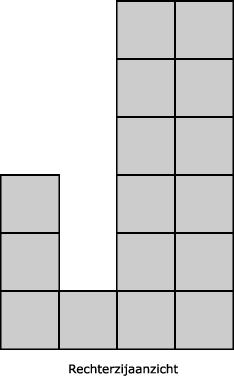
12.
Zie afbeelding
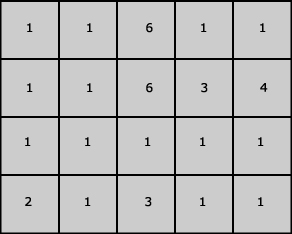
13.
Zie afbeelding
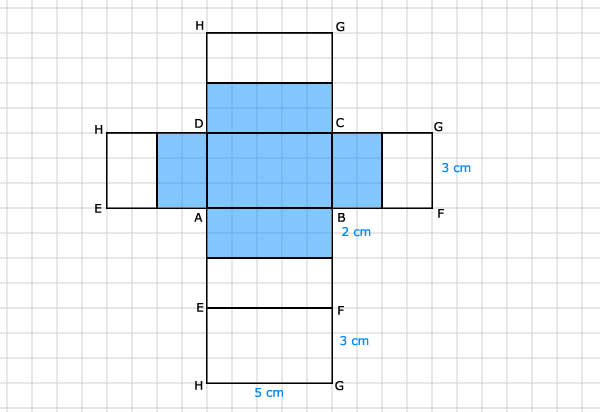
14.
Zie afbeelding opgave 13.
15.
Figuur b. De uitslag hoort bij een halve cilinder (cirkel) met diameter is 2. En c. heeft een diameter van 3.
16.
Zie afbeelding
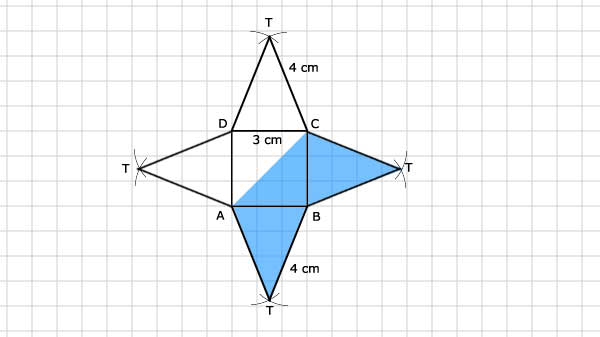
17.
Zie afbeelding bij opgave 16.
18.
Zie afbeelding
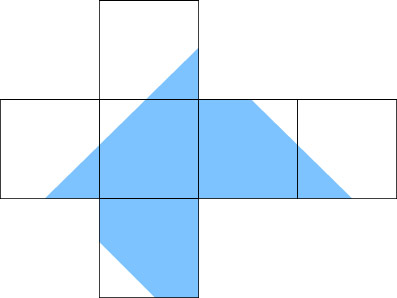
19.
Oppervlakte 1 vlak is 4 m2. Oppervlakte blauw = (6 x 4) / 2 = 12 m2
20.
Oppervlakte van de cilinder: 25,1 cm2
Oppervlakte van de halve cilinder: 22,5 cm2
Zie afbeelding

12.
Zie afbeelding

13.
Zie afbeelding

14.
Zie afbeelding opgave 13.
15.
Figuur b. De uitslag hoort bij een halve cilinder (cirkel) met diameter is 2. En c. heeft een diameter van 3.
16.
Zie afbeelding

17.
Zie afbeelding bij opgave 16.
18.
Zie afbeelding

19.
Oppervlakte 1 vlak is 4 m2. Oppervlakte blauw = (6 x 4) / 2 = 12 m2
20.
Tip:
Bij de piramide: maak een schets van driehoek ABT en trek TQ loodrecht op AB. Dan geldt: AQ = BQ = 2.
Doe hetzelfde bij driehoek BCT, trek loodlijn uit T. Bereken van beide loodlijnen de hoogte met de Stelling van Pythagoras en bepaal zo de oppervlakte van de 4 driehoeken m.b.v ½ x basis x hoogte.
Bij de cilinder: bepaal de omtrek van de cirkel en gebruik deze als lengte van de cilindermantel.
Oppervlakte van de piramide: 44,6 cm2Bij de piramide: maak een schets van driehoek ABT en trek TQ loodrecht op AB. Dan geldt: AQ = BQ = 2.
Doe hetzelfde bij driehoek BCT, trek loodlijn uit T. Bereken van beide loodlijnen de hoogte met de Stelling van Pythagoras en bepaal zo de oppervlakte van de 4 driehoeken m.b.v ½ x basis x hoogte.
Bij de cilinder: bepaal de omtrek van de cirkel en gebruik deze als lengte van de cilindermantel.
Oppervlakte van de cilinder: 25,1 cm2
Oppervlakte van de halve cilinder: 22,5 cm2
21.
Bereken eerst AC met de Stelling van Pythagoras. AC = √73 ≈ 8,5.
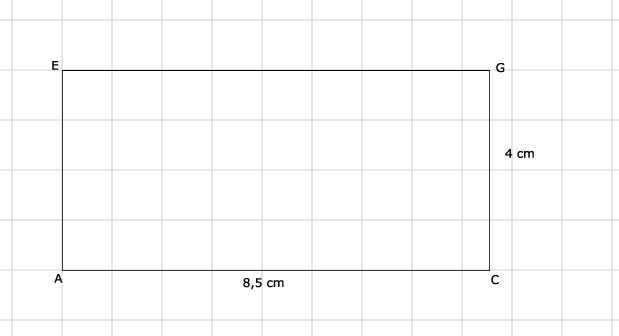
22.
Nee, diagonaalvlak ABGH heeft andere afmetingen dan diagonaalvlak ACGE.
23.
Bereken eerst AQ met de Stelling van Pythagoras. AQ = √34 ≈ 5,8.
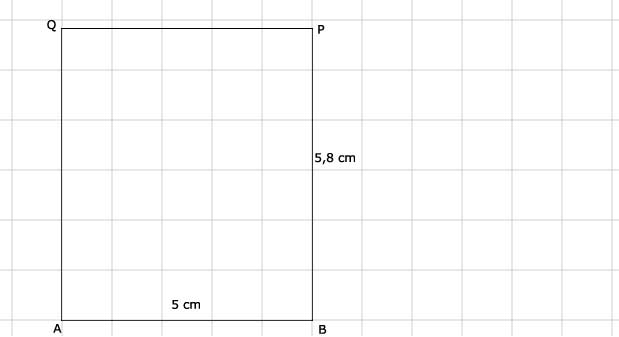
24.
Met Stelling van Pythagoras bereken je de zijde van de zeshoek. Deze is √8 ≈ 2,8.
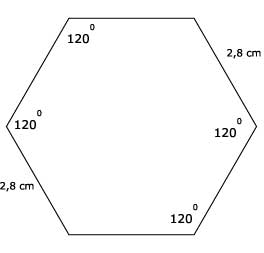
25.
Bereken eerst AC en gebruik dan de tangens.
∠GAC = 25º
26.
27.
28.
BH ≈ 15,1 cm
29.
CM ≈ 13,4 cm
30.
Lengte rietje binnen het blikje is √170 ≈ 13,0 cm. Dan lengte rietje = 13,0 + 5 = 18 cm.
Bereken eerst AC met de Stelling van Pythagoras. AC = √73 ≈ 8,5.

22.
Nee, diagonaalvlak ABGH heeft andere afmetingen dan diagonaalvlak ACGE.
23.
Bereken eerst AQ met de Stelling van Pythagoras. AQ = √34 ≈ 5,8.

24.
Met Stelling van Pythagoras bereken je de zijde van de zeshoek. Deze is √8 ≈ 2,8.

25.
Bereken eerst AC en gebruik dan de tangens.
∠GAC = 25º
26.
Tip:
Bereken eerst lengte rietje in het glas met: h = 6 : cos(59º). Dat is 11,6 cm. Dan 15 - 11,6 = 3,4 cm.
Hoogte glas bereken je met 6 x tan(59º).
Het rietje steekt 3,4 cm boven het glas uit. Het glas is 10 cm hoog. Bereken eerst lengte rietje in het glas met: h = 6 : cos(59º). Dat is 11,6 cm. Dan 15 - 11,6 = 3,4 cm.
Hoogte glas bereken je met 6 x tan(59º).
27.
Tip:
Neem H het midden van EF. Bereken dan EH met de tangens. Dan AB = 2 x EH.
AB = 9,2 cmNeem H het midden van EF. Bereken dan EH met de tangens. Dan AB = 2 x EH.
28.
BH ≈ 15,1 cm
29.
CM ≈ 13,4 cm
30.
Lengte rietje binnen het blikje is √170 ≈ 13,0 cm. Dan lengte rietje = 13,0 + 5 = 18 cm.
31.
196,8 meter
32.
We zien 3 hoogtelijnen: 330 feet, 395 feet en 265 feet. In meters: 99 meter, 118,5 meter en 79,5 meter. (steeds 0,3 keer)
33.
Nee, want hoogtelijn 500 is niet getekend in dat gebied.
34.
Arceer als het hoogste gebied bij punt A (500) / bergtop.
35.
400 meter
36.
37.
Nee, Rienk kan de hut niet zien.
38.
*
39.
D(200, 200, 400)
40.
B(150, 255, 490)
C(355, 255, 480)
P(300, 105, 350)
Q(205, 280, 400)
Y(100, 50, 350)
Z(410, 60, 350)
196,8 meter
32.
We zien 3 hoogtelijnen: 330 feet, 395 feet en 265 feet. In meters: 99 meter, 118,5 meter en 79,5 meter. (steeds 0,3 keer)
33.
Nee, want hoogtelijn 500 is niet getekend in dat gebied.
34.
Arceer als het hoogste gebied bij punt A (500) / bergtop.
35.
400 meter
36.
Tip:
Maak een driehoek PQR, met hoek R is recht en QR = 50 en PQ is de schuine zijde (203,1 meter). Gebruik dan de sinus.
∠P ≈ 14ºMaak een driehoek PQR, met hoek R is recht en QR = 50 en PQ is de schuine zijde (203,1 meter). Gebruik dan de sinus.
37.
Nee, Rienk kan de hut niet zien.
38.
*
39.
D(200, 200, 400)
40.
B(150, 255, 490)
C(355, 255, 480)
P(300, 105, 350)
Q(205, 280, 400)
Y(100, 50, 350)
Z(410, 60, 350)
41.
42.
Hoekpunt C hoort bij (0, 6, 0)
43.
Hoekpunt F hoort bij (6, 6, 4)
44.
Snijpunt S hoort bij (3, 3, 4)
45.
Q ligt op de balk (achterwand)
R ligt binnen de balk
S ligt op de balk (plafond)
T ligt binnen de balk
46.
47.
Inhoud clinder = 9 cm3
Inhoud halve clinder = 7 cm3
48.
49.
50.
Tip:
Tussen P(300, 105, 350) en C(355, 255, 480) is het verschil in de x-richting: 55, in de y-richting: 150 en in de z-richting: 130. Gebruik de verlengde Stelling van Pythagoras.
Kabelbaan wordt: √42 425 ≈ 205,97 meter.Tussen P(300, 105, 350) en C(355, 255, 480) is het verschil in de x-richting: 55, in de y-richting: 150 en in de z-richting: 130. Gebruik de verlengde Stelling van Pythagoras.
42.
Hoekpunt C hoort bij (0, 6, 0)
43.
Hoekpunt F hoort bij (6, 6, 4)
44.
Snijpunt S hoort bij (3, 3, 4)
45.
Q ligt op de balk (achterwand)
R ligt binnen de balk
S ligt op de balk (plafond)
T ligt binnen de balk
46.
Tip:
Inhoud cilinder = oppervlakte grondvlak x hoogte en oppervlakte grondvlak is π x r2
Inhoud blikje = 499,22 cm3 ≈ 0,5 literInhoud cilinder = oppervlakte grondvlak x hoogte en oppervlakte grondvlak is π x r2
47.
Inhoud clinder = 9 cm3
Inhoud halve clinder = 7 cm3
48.
Tip:
Inhoud piramide = 1/3 x oppervlakte grondvlak x hoogte
4500 m3Inhoud piramide = 1/3 x oppervlakte grondvlak x hoogte
49.
Tip:
Inhoud balk = lengte x breedte x hoogte
Reken eerst alles terug naar cm!
Inhoud balk = 8000 cm3Inhoud balk = lengte x breedte x hoogte
Reken eerst alles terug naar cm!
50.
Tip:
Tent is een prisma. Inhoud prisma = [ oppervlakte grondvlak ] x hoogte = [ oppervlakte driehoek ] x hoogte
Inhoud tent = 3,45 m3Tent is een prisma. Inhoud prisma = [ oppervlakte grondvlak ] x hoogte = [ oppervlakte driehoek ] x hoogte
51.
Inhoud zwembad: 59,375 m3 = 593 750 liter
52.
53.
3817 cm3 ≈ 3,8 liter
54.
1885 cm3
55.
38,2 cl
56.
Inhoud rode pot = 1,6875 liter
57.
43 = 64 porties
58.
Schaal is 1 : 250
59.
Breedte doos B ≈ 28 cm.
60.
Figuur A wordt een kubus
Figuur B wordt een balk
Figuur C wordt een piramide
Figuur D wordt een prisma
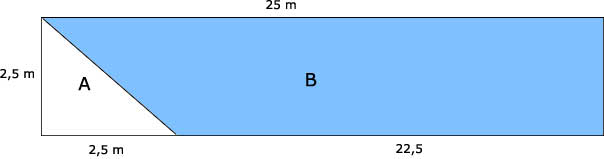
Tip:
Bereken [ oppervlakte rechthoek - oppervlakte witte driehoek ]. Je houdt oppervlakte blauwe figuur B over. Vermenigvuldig dat met 10 en je hebt de inhoud van het zwembad.
Oppervlakte blauw B = (2,50 x 25) - (1/2 x 2,2 x 2,5)Bereken [ oppervlakte rechthoek - oppervlakte witte driehoek ]. Je houdt oppervlakte blauwe figuur B over. Vermenigvuldig dat met 10 en je hebt de inhoud van het zwembad.
Inhoud zwembad: 59,375 m3 = 593 750 liter

52.
Tip:
Bereken inhoud baksteen en haal daar de inhoud van 10 kleine cilinders vanaf. Bedenk: straal (r) cilinder = 0,75 cm.
873,3 cm3Bereken inhoud baksteen en haal daar de inhoud van 10 kleine cilinders vanaf. Bedenk: straal (r) cilinder = 0,75 cm.
53.
3817 cm3 ≈ 3,8 liter
54.
1885 cm3
55.
38,2 cl
56.
Tip:
Bereken steeds de vergrotingsfactor van de ene naar de andere pot.
Inhoud gele pot = 0,864 literBereken steeds de vergrotingsfactor van de ene naar de andere pot.
Inhoud rode pot = 1,6875 liter
57.
43 = 64 porties
58.
Schaal is 1 : 250
59.
Breedte doos B ≈ 28 cm.
60.
Figuur A wordt een kubus
Figuur B wordt een balk
Figuur C wordt een piramide
Figuur D wordt een prisma
61.
*
62.
B = 7 plakranden
C = 4 plakranden
D = 5 plakranden
63.
Ja, de formule klopt.
64.
Inhoud van figuur A = 125 cm3
Inhoud van figuur B = 81 cm3
Inhoud van figuur C = 107,67 cm3
Inhoud van figuur D = 129,90 cm3
65.
66.
67.
Vergrotingsfactor ≈ 1,26, namelijk √ (5 / 3,14) ≈ 1,26.
68.
69.
A(2, 1, 1)
B(2, 2, 0)
C(1, 2, 2)
D(0, 1, 2)
E(1, 3, 1)
F(0, 0, 1)
G(1, 0, 1)
H(2, 0, 0)
70.
BF = √900 = 30 cm
*
62.
B = 7 plakranden
C = 4 plakranden
D = 5 plakranden
63.
Ja, de formule klopt.
64.
Inhoud van figuur A = 125 cm3
Inhoud van figuur B = 81 cm3
Inhoud van figuur C = 107,67 cm3
Inhoud van figuur D = 129,90 cm3
65.
Tip:
Bereken inhoud van cilinder met straal = 0,375 meter.
Inhoud van de kolom is 1,1 m3.Bereken inhoud van cilinder met straal = 0,375 meter.
66.
Tip:
Bedenk dat diameter raam ongeveer 2 meter is.
Oppervlakte raam ≈ 3,14 m2Bedenk dat diameter raam ongeveer 2 meter is.
67.
Vergrotingsfactor ≈ 1,26, namelijk √ (5 / 3,14) ≈ 1,26.
68.
Tip:
Hellingspercentage = tan(van de hoek) x 100%
Hellingspercentage = 21%Hellingspercentage = tan(van de hoek) x 100%
69.
A(2, 1, 1)
B(2, 2, 0)
C(1, 2, 2)
D(0, 1, 2)
E(1, 3, 1)
F(0, 0, 1)
G(1, 0, 1)
H(2, 0, 0)
70.
BF = √900 = 30 cm
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


