TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Uitwerking 6.3 Berekeningen met de stelling van Pythagoras opgave 38
01-07-2025
admin
Getal & Ruimte HAVO/VWO 2 (deel 2) hoofdstuk 6 De stelling van Pythagoras
Uitleg
Om afstanden in een assenstelsel tussen twee roosterpunten te bepalen, zoeken we eerst een rechte hoek in een rechthoekige driehoek. Bepaal daarna de rechthoekszijden.
Vraag 38
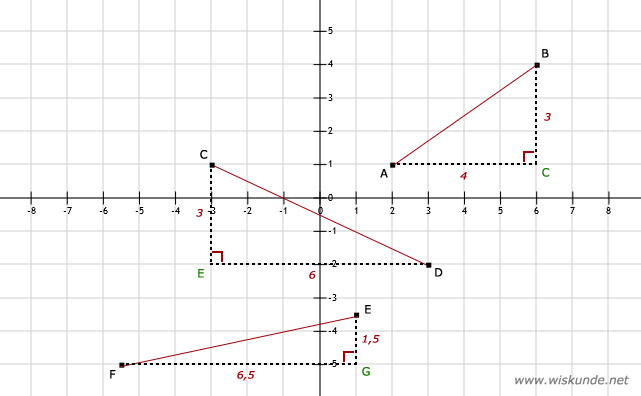
Gegeven een assenstelsel met daarin de punten A, B t/m F. Gevraagd om de afstand tussen diverse punten te berekenen.
Antwoord
|
a. AC(kwadraat) + BC(kwadraat) = AB(kwadraat) 4(kwadraat) + 3(kwadraat) = AB(kwadraat) AB(kwadraat) = 16 + 9 AB(kwadraat) = 25 AB = (wortel)25 AB = 5 |
b. DE(kwadraat) + CE(kwadraat) = CD(kwadraat) 6(kwadraat) + 3(kwadraat) = CD(kwadraat) CD(kwadraat) = 36 + 9 CD(kwadraat) = 45 CD = (wortel)45 CD (ongeveer) 6,71 |
FG(kwadraat) + EG(kwadraat) = EF(kwadraat)
6,5(kwadraat) + 1,5(kwadraat) = EF(kwadraat)
EF(kwadraat) = 44,5
EF = (wortel)44,5
EF (ongeveer) 6,67
Uitwerking
a.
AP2 + BP2 = AB2
42 + 32 = AB2
AB2 = 16 + 9
AB2 = 25
AB = √25 = 5
b.
CQ2 + DQ2 = CD2
32 + 62 = CD2
CD2 = 9 + 36
CD2 = 45
CD = √45 ≈ 6,71
c.
ER2 + FR2 = EF2
1,52 + 6,52 = EF2
EF2 = 2,25 + 42,25
EF2 = 44,5
EF = √44,5 ≈ 6,67
Reageer op deze uitwerking
Heb je een vraag over deze opgave, snap je iets niet of ben je een fout tegengekomen en wil je binnen 10 minuten antwoord? Stel een vraag!