Uitwerking 6.2 Het berekenen van schuine zijden opgave 21
01-06-2025
admin
Getal & Ruimte HAVO/VWO 2 (deel 2) hoofdstuk 6 De stelling van Pythagoras
Uitleg
Bedenk: knip de cilinder over de hoogte door. Je krijgt dan een rechthoek. Deze rechthoek heeft een schuine ziijde in het midden. (diagonaal). Deze diagonaal is het rode touwtje. Gebruik omtrek cirkel = π x diameter om de lengte van de mantel (rechthoek) te berekenen. De hoogte is bekend. Via de Stelling van Pythagoras bereken je de lengte van het touwtje (schuine zijde).
Vraag 21
Gegeven een cilinder met een rood touwtje dat gaat om de cilinder heen van A naar B. Bereken de lengte van het touwtje.
Antwoord
Bereken eerst AB.
AB = omtrek cirkel = π x diameter
AB = π x 9
AB (ongeveer) 28,3 cm
AB(kwadraat) + BC(kwadraat) = AC(kwadraat)
28,3(kwadraat) + 21(kwadraat) = AC(kwadraat)
AC(kwadraat) = 1241,89
AC = (wortel)1241,89
AC (ongeveer) 35,24 cm
Dus de lengte van het rode touwtje is 352 mm.
Uitwerking
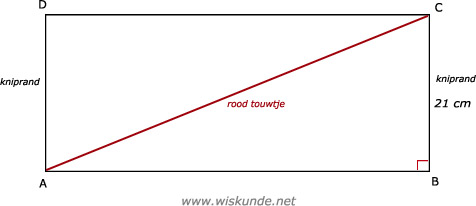
De omtrek van de grondcirkel van de cilinder is: diameter x π = 9π
Bekijk de afbeelding, dan kun je AC (het rode touwtje) berekenen met de Stelling van Pythagoras:
AB2 + BC2 = AC2
(9π)2 + 212 = AC2
AC2 = 81π2 + 441
AC2 = 1240,437956
AC ≈ 35,22 cm
Dus lengte rode touw is dus ongeveer 352 mm.
Reageer op deze uitwerking
Heb je een vraag over deze opgave, snap je iets niet of ben je een fout tegengekomen en wil je binnen 10 minuten antwoord? Stel een vraag!