Uitwerking 3.2 De top van een parabool opgave 19
01-06-2025
admin
Getal & Ruimte HAVO 3 (deel 1) hoofdstuk 3 Kwadratische problemen
Uitleg
Om de top van een parabool ax2 + bx + c, met a ongelijk 0 te berekenen, gebruiken we:
Xtop = -( b / 2a). Daarnaast
Ytop krijg je door Xtop in de formule in te vullen.
Bij een dalparabool geldt: a > 0. Bij een bergparabool geldt: a < 0.
Vraag 19
Bereken de coordinaten van de top van de volgende grafieken / parabolen:
a. y = x2 + 4x + 1
b. y = -x2 + 2x + 10
c. y = 1,2x2 - 8,4x + 1,3
b. y = -0,25x2 + 4x - 17
Antwoord
a.
a = 1, b = 4, c = 1
Xtop = -b / 2a = -4/2 = -2
Ytop => y = (-2)(kwadraat) + 4 ⋅ -2 + 1 = 4 - 8 + 1 = -3
Dus de top van deze parabool is: Top(-2,-3)
b.
a = -1, b = 2, c = 10
Xtop = -b / 2a = -2/-2 = 1
Ytop => y = -(1)(kwadraat) + 2 ⋅ 1 + 10 = -1 + 2 + 10 = 11
Dus de top van deze parabool is: Top(1,11)
c.
a = 1,2, b = -8,4, c = 1,3
Xtop = -b / 2a = 8,4/2,4 = 3,5
Ytop => y = 1,2 ⋅ (3,5)(kwadraat) - 8,4 ⋅ 3,5 + 1,3 = 14,7 - 29,4 + 1,3 = -13,4
Dus de top van deze parabool is: Top(3,5 ; -13,4)
d.
a = -0,25, b = 4, c = -17
Xtop = -b / 2a = -4/-0,5 = 8
Ytop => y = -0,25 ⋅ (8)(kwadraat) + 4 ⋅ 8 - 17 = -0,25 ⋅ 64 + 32 - 17 = -16 + 32 - 17 = -1
Dus de top van deze parabool is: Top(8,-1)
Uitwerking
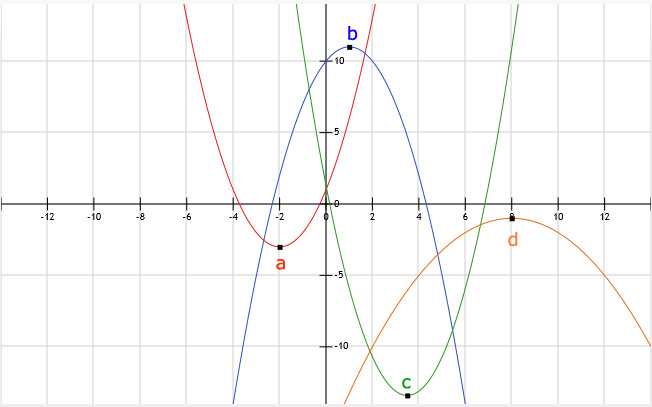
a.
Gegeven y = x2 + 4x + 1, dus dan is a = 1 en b = 4.
Xtop = -(b/2a) = -(4/2) = -(2) = -2.
Ytop => invullen in de functie => y = (-2)2 + 4 ⋅ -2 + 1 = 4 - 8 + 1 = -3.
De top van de parabool is dus T(-2,-3).
b.
Gegeven y = -x2 + 2x + 10, dus dan is a = -1 en b = 2.
Xtop = -(b/2a) = -(2/-2) = -(-1) = 1.
Ytop => invullen in de functie => y = -(1)2 + 2 ⋅ 1 + 10 = -1 + 2 + 10 = 11.
De top van de parabool is dus T(1,11).
c.
Gegeven y = 1,2x2 - 8,4x + 1,3, dus dan is a = 1,2 en b = -8,4.
Xtop = -(b/2a) = -(-8,4/2,4) = -(-3,5) = 3,5.
Ytop => invullen in de functie => y = 1,2 ⋅ (3,5)2 - 8,4 ⋅ 3,5 + 1,3 = 14,7 - 29,4 + 1,3 = -13,4.
De top van de parabool is dus T(3,5;-13,4).
d.
Gegeven y = -0,25x2 + 4x - 17, dus dan is a = -0,25 en b = 4.
Xtop = -(b/2a) = -(4/-0,5) = -(-8) = 8.
Ytop => invullen in de functie => y = -0,25 ⋅ (8)2 + 4 ⋅ 8 - 17 = -16 + 32 - 17 = -1.
De top van de parabool is dus T(8,-1).
Reageer op deze uitwerking
Heb je een vraag over deze opgave, snap je iets niet of ben je een fout tegengekomen en wil je binnen 10 minuten antwoord? Stel een vraag!