Wiskunde.netLogo Wiskunde


Video uitwerking §4.3 Gebroken vormen: opgave 60 - (7:06)

Boek: Getal & Ruimte - Werken met formules HAVO 4 (deel 1) 12e editie, 2020

Je kunt nú 1 minuut kijken. Word lid om 16.000 video-uitwerkingen in z'n geheel te bekijken. Klik hier...


Rate deze video:
Rating is 5 / 5.
Aantal stemmen: 1 keer.
Heb je een vraag of opmerking over deze video?
Laat ons weten wat je van deze video en Wiskunde.net vindt. Ben je tevreden? We horen het graag! Klik hier om je opmerking te plaatsen...
   
Opgave 56
Gebroken vormen opgave 56 		Opgave 59
Gebroken vormen opgave 59 		Opgave 60
Gebroken vormen opgave 60 		Opgave 61
Gebroken vormen opgave 61

Gebroken functies Gebroken vergelijkingen
×

Geel uitlegblok per bladzijde:
Blz 156: Gebroken functies (09:34)
Blz 158: Gebroken vergelijkingen (13:03)
Andere paragrafen:
4.0. Voorkennis (1 t/m 4)
4.1. Kwadratische formules (1 t/m 27)
4.2. Hogeregraadsvergelijkingen en ongelijkheden (28 t/m 51)
4.3. Gebroken vormen (52 t/m 61)
4.4. Extreme waarden en wiskundige modellen (62 t/m 77)
4.5. D-toets (1 t/m 14)
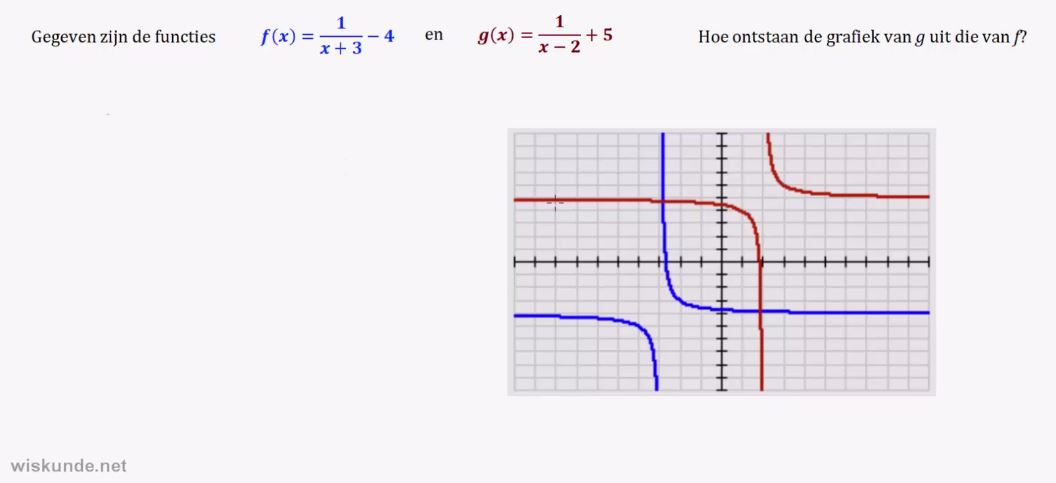
Leerdoelen paragraaf: Gebroken vormen:
1. Een gebroken functie herkennen en weten wat een hyperbool is.
2. De eenvoudigste gebroken functie kennen f(x) = 1/x.
3. De horizontale- en verticale asymptoot kunnen opschrijven bij een gebroken functie.
4. Een translatie met een hyperbool kunnen uitvoeren.
5. Gebroken vergelijkingen kunnen oplossen.
6. De regels van gebroken vergelijkingen kunnen toepassen.
7. Breuken kunnen herleiden en uitdelen.
8. Gebroken formules kunnen omwerken.
Oefenen met Geogebra...

Geef je mening aan ons:
Review
Tevreden? Laat het ons weten!
Schrijf een review...
Jurgen de Bont Foto: Jurgen de Bont - Docent Wiskunde - Breda   
Welkom leerlingen op Wiskunde.net!   

Op deze site vind je duidelijke uitlegvideo's gekoppeld aan jouw boek om jou verder te helpen met het mooie vak Wiskunde. Hierboven vind je de video-uitleg van §4.3 Gebroken vormen opgave 60 en links in het gele blokje (indien aanwezig), kun je de theorie bekijken in video. Ben je nog geen lid? Klik dan hier...
Succes verzekerd!

Met wiskundige groet,
Jurgen de Bont & Martijn Claassen & Bob Pruiksma, docenten Wiskunde onder- en bovenbouw