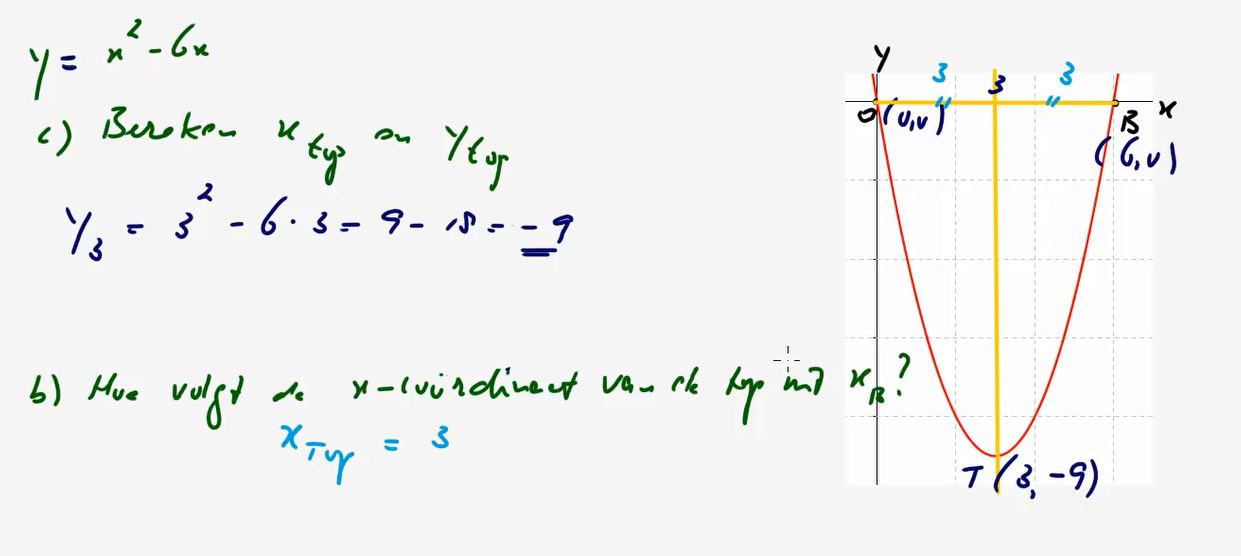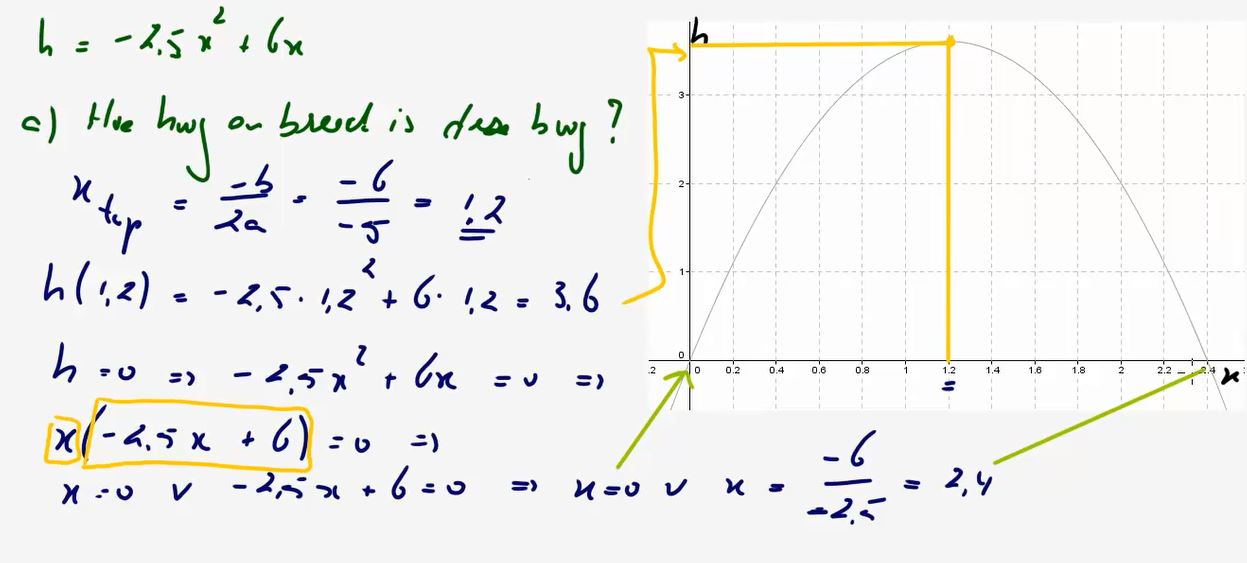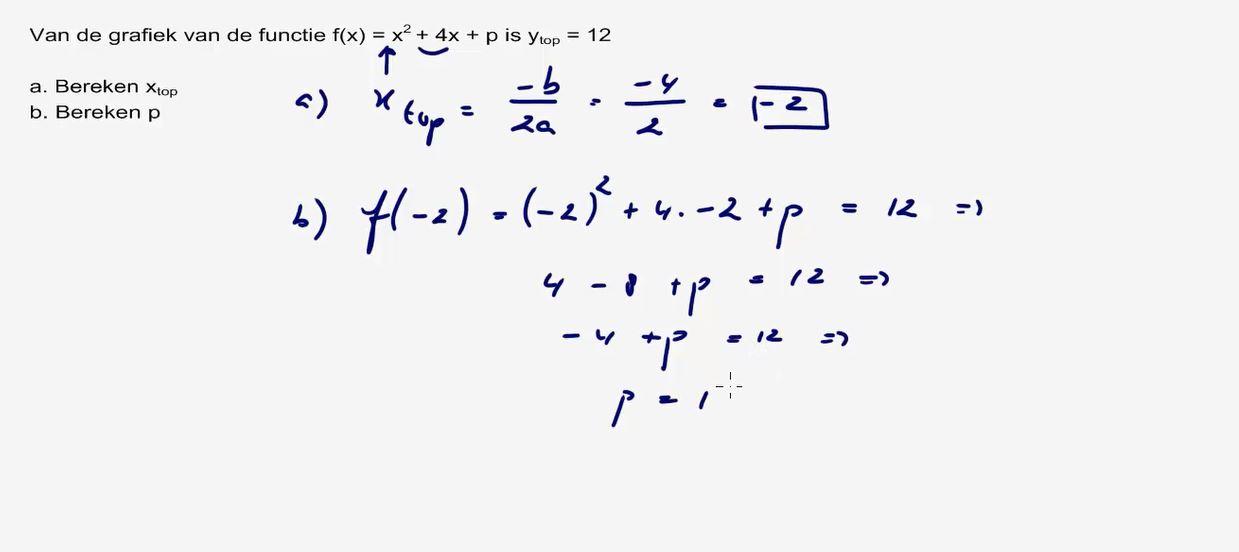Wiskunde.netLogo Wiskunde


Video uitwerking §3.5 De top van de parabool y = ax2 + bx + c: opgave 65 - (5:01)

Boek: Getal & Ruimte - Kwadratische problemen HAVO 3 (deel 1) 10e editie, 2014

Je kunt nú 1 minuut kijken. Word lid om 16.000 video-uitwerkingen in z'n geheel te bekijken. Klik hier...


Rate deze video:
Rating is 4.1 / 5.
Aantal stemmen: 15 keer.
Helaas zit er een fout in de video. Bij opgave b. moet de diepte van de tunnel niet 8 meter zijn, maar 20 meter.
Heb je een vraag of opmerking over deze video?
Laat ons weten wat je van deze video en Wiskunde.net vindt. Ben je tevreden? We horen het graag! Klik hier om je opmerking te plaatsen...
   
Opgave 58
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 58 		Opgave 59
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 59 		Opgave 60
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 60 		Opgave 61
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 61 		Opgave 62
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 62 		Opgave 63
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 63 		Opgave 64
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 64 		Opgave 65
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 65
Opgave 66
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 66 		Opgave 67
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 67 		Opgave 68
De top van de parabool y = ax<sup>2</sup> + bx + c opgave 68

Andere paragrafen:
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 30)
3.3. De parabool y = a(x - d)(x - e) (31 t/m 43)
3.4. De parabool y = a(x - p)2 + q (44 t/m 57)
3.5. De top van de parabool y = ax2 + bx + c (58 t/m 68)
Leerdoelen paragraaf: De top van de parabool y = ax2 + bx + c:
1. De top van een parabool kunnen berekenen.
2. De basisformule van een parabool y = ax2 + bx + c kennen en kunnen opschrijven.
3. De Xtop van een parabool kunnen berekenen met -b/2a.
4. De Ytop kunnen berekenen door de Xtop in te vullen in de formule.
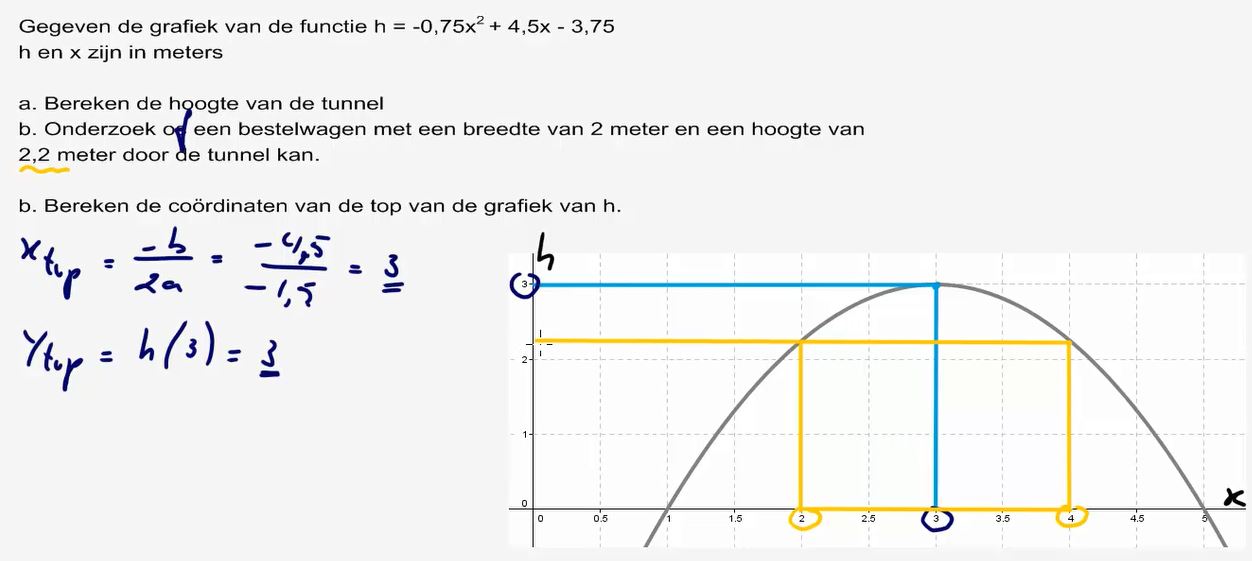
5. De hoogte en breedte van bogen kunnen berekenen.
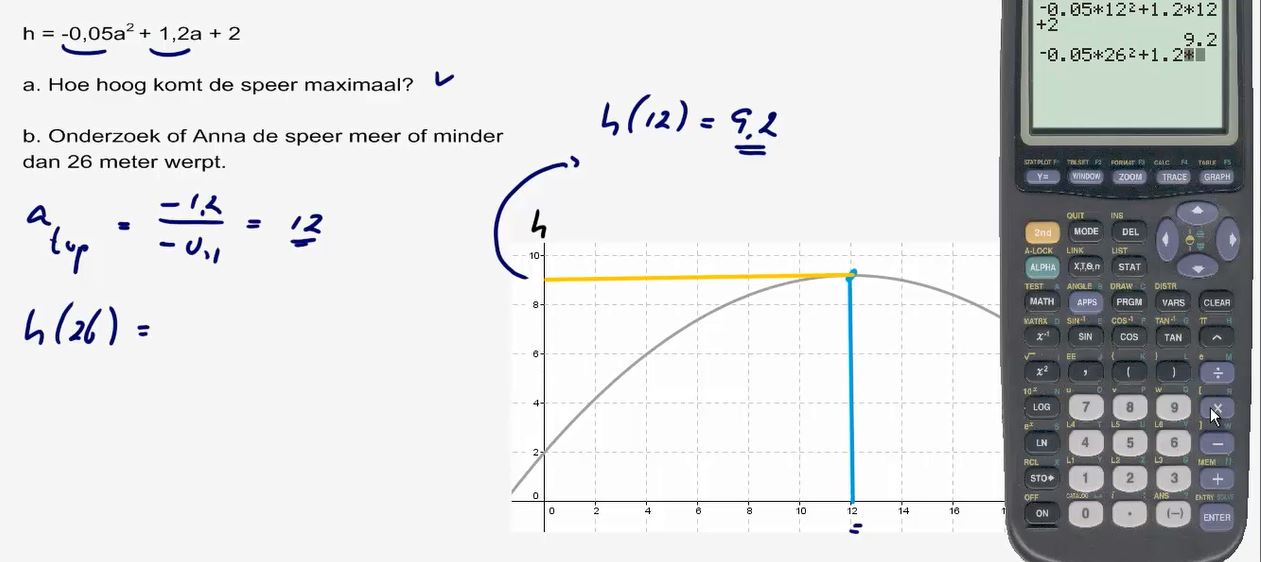
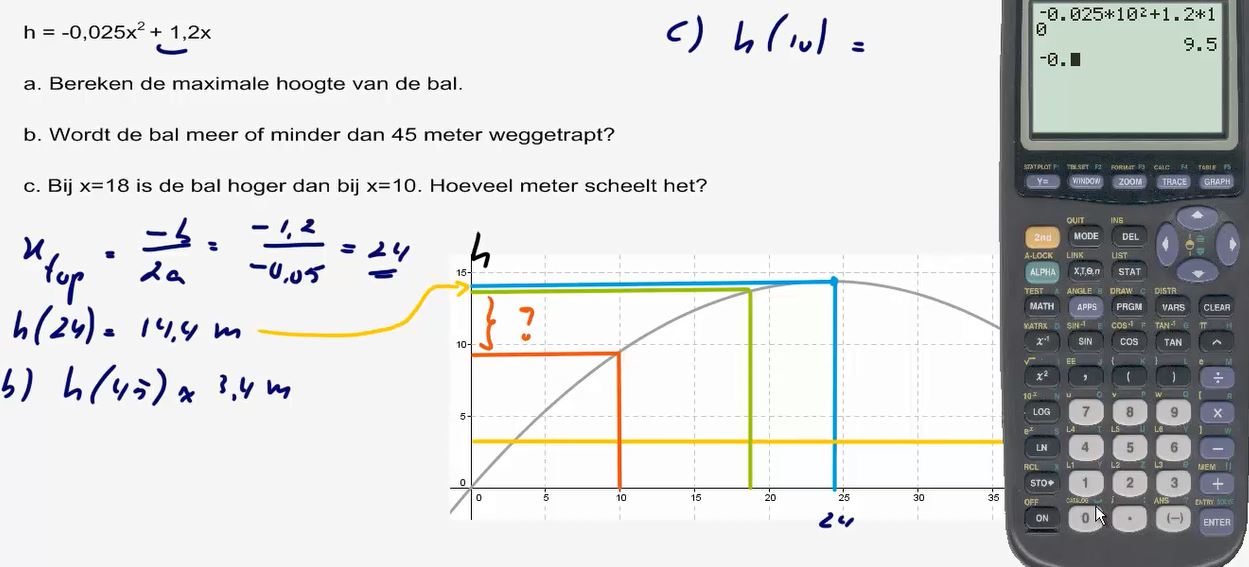
6. Kunnen berekenen wanneer een bal weer op de grond komt.
7. Onderzoeken of een bestelwagen door een tunnel kan.
Oefenen met Geogebra...

Geef je mening aan ons:
Review
Tevreden? Laat het ons weten!
Schrijf een review...
Jurgen de Bont Foto: Jurgen de Bont - Docent Wiskunde - Breda   
Welkom leerlingen op Wiskunde.net!   

Op deze site vind je duidelijke uitlegvideo's gekoppeld aan jouw boek om jou verder te helpen met het mooie vak Wiskunde. Hierboven vind je de video-uitleg van §3.5 De top van de parabool y = ax2 + bx + c opgave 65 en links in het gele blokje (indien aanwezig), kun je de theorie bekijken in video. Ben je nog geen lid? Klik dan hier...
Succes verzekerd!

Met wiskundige groet,
Jurgen de Bont & Martijn Claassen & Bob Pruiksma, docenten Wiskunde onder- en bovenbouw