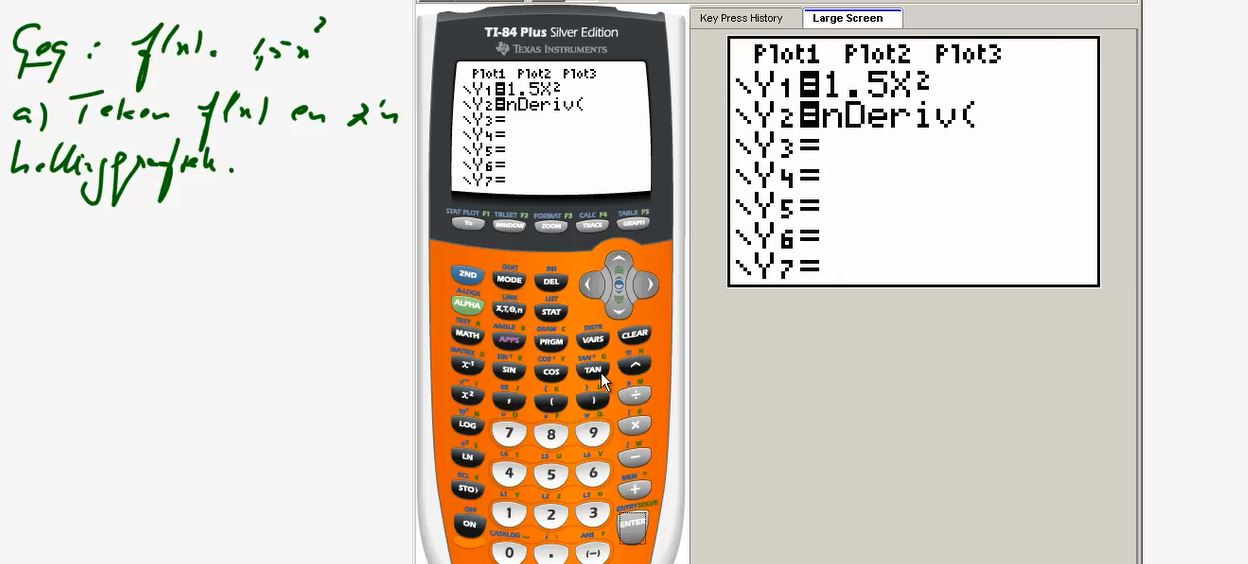
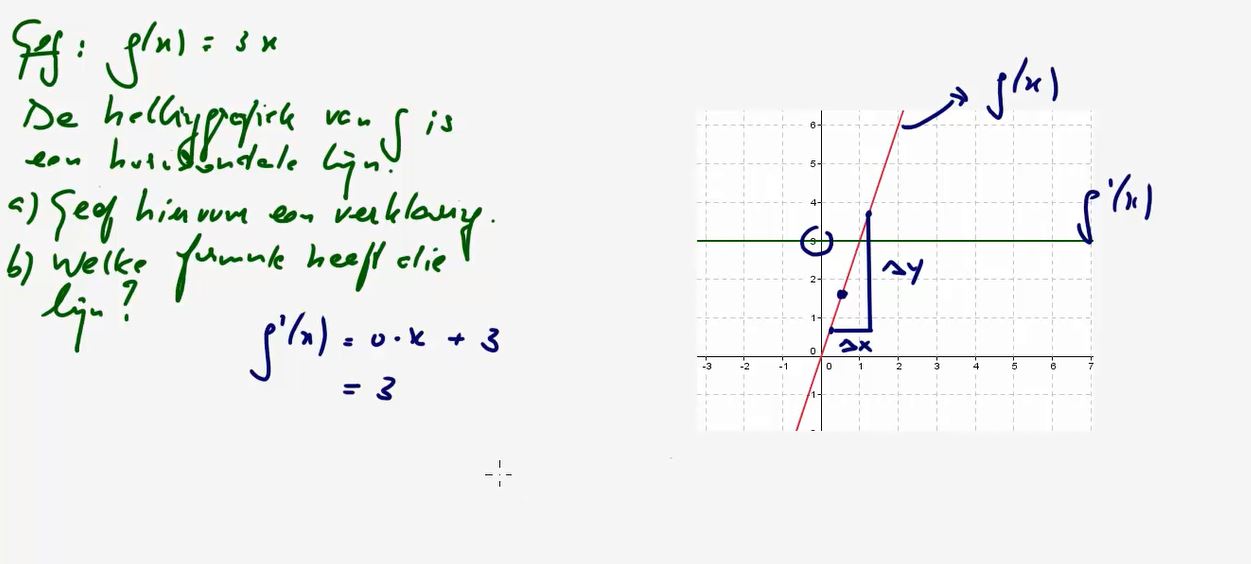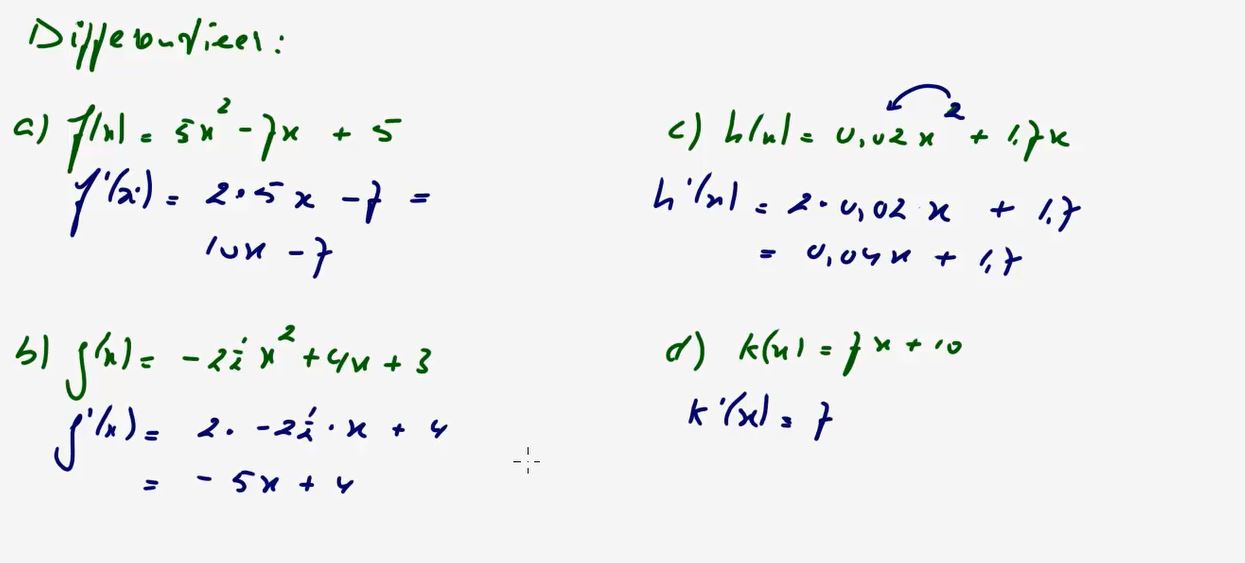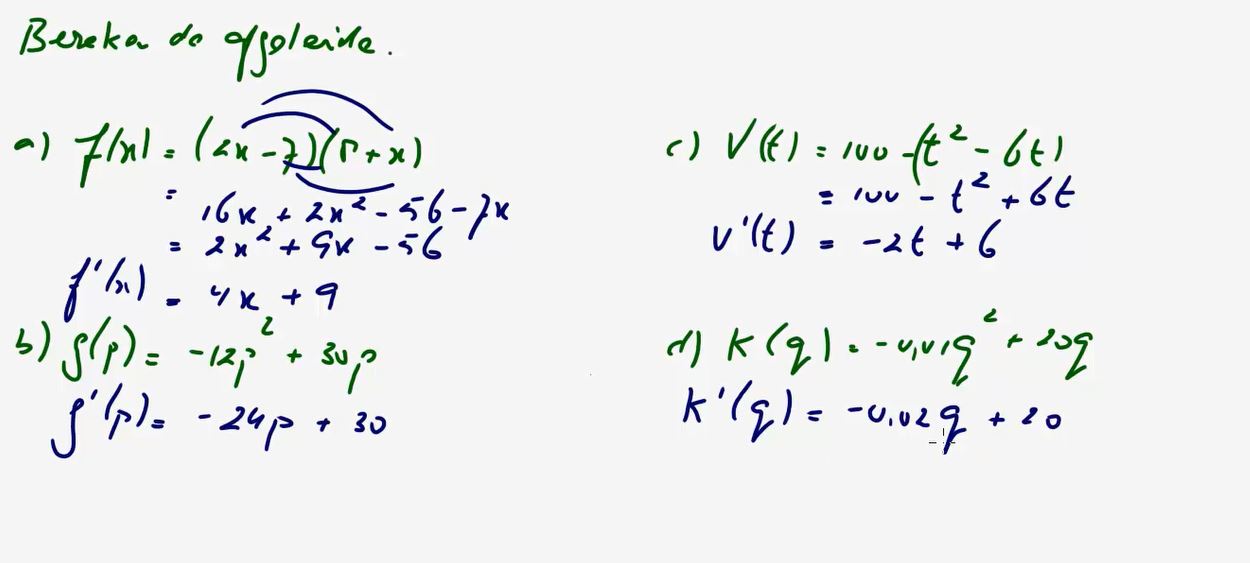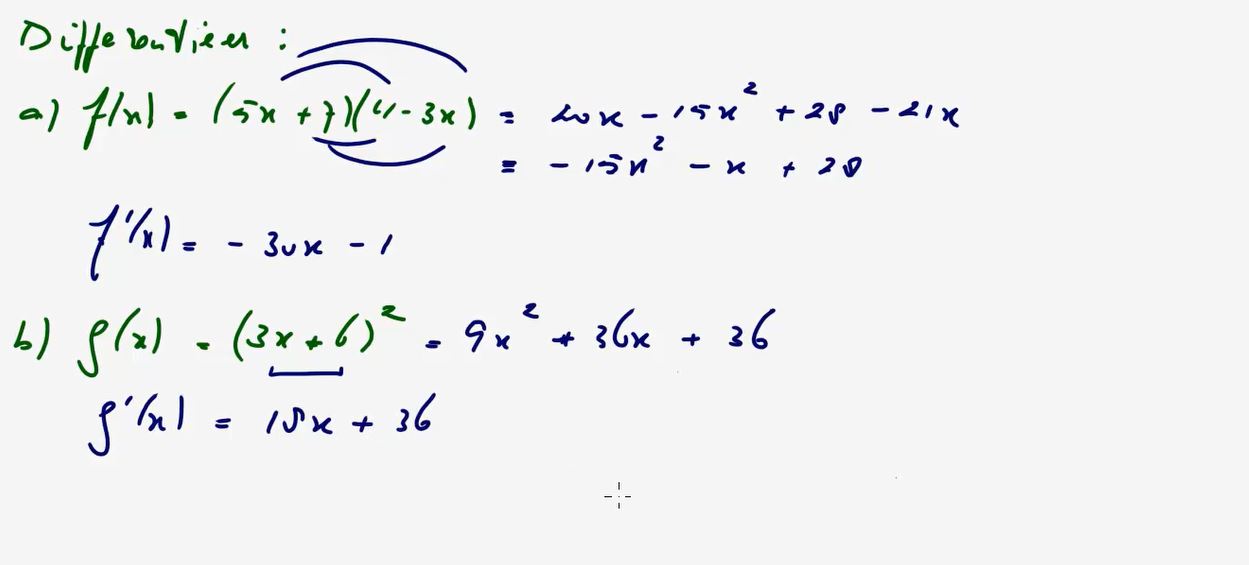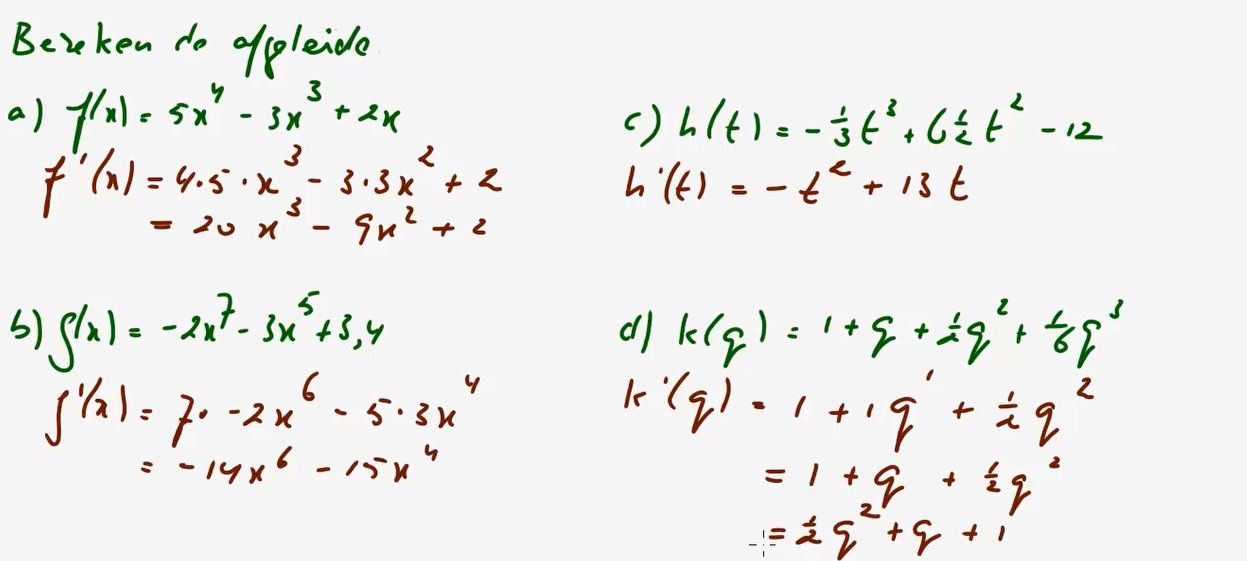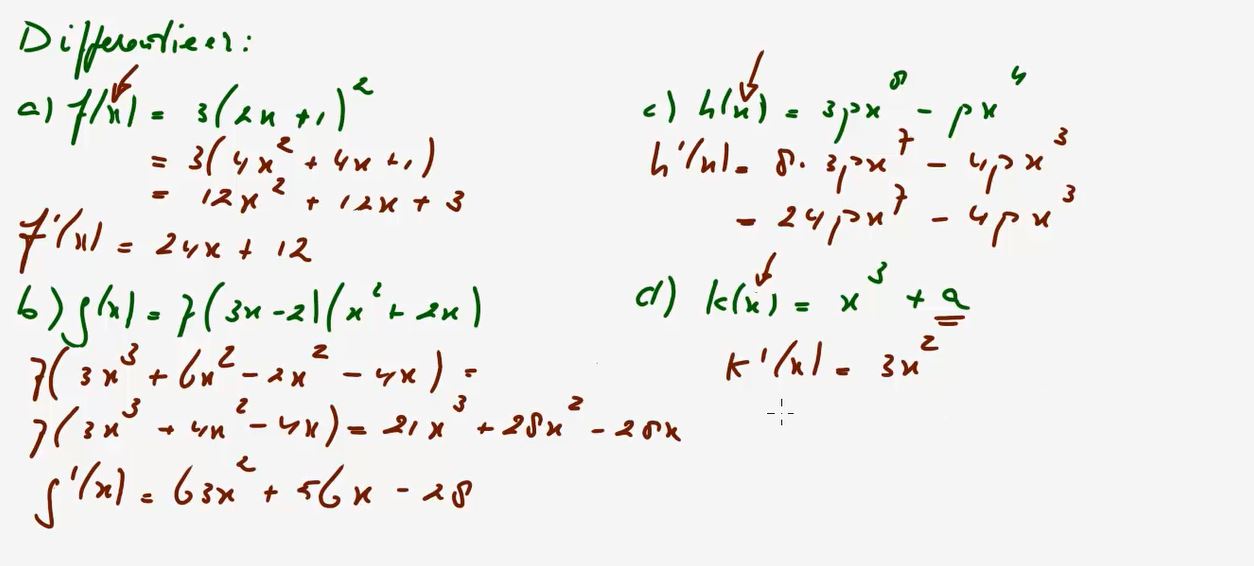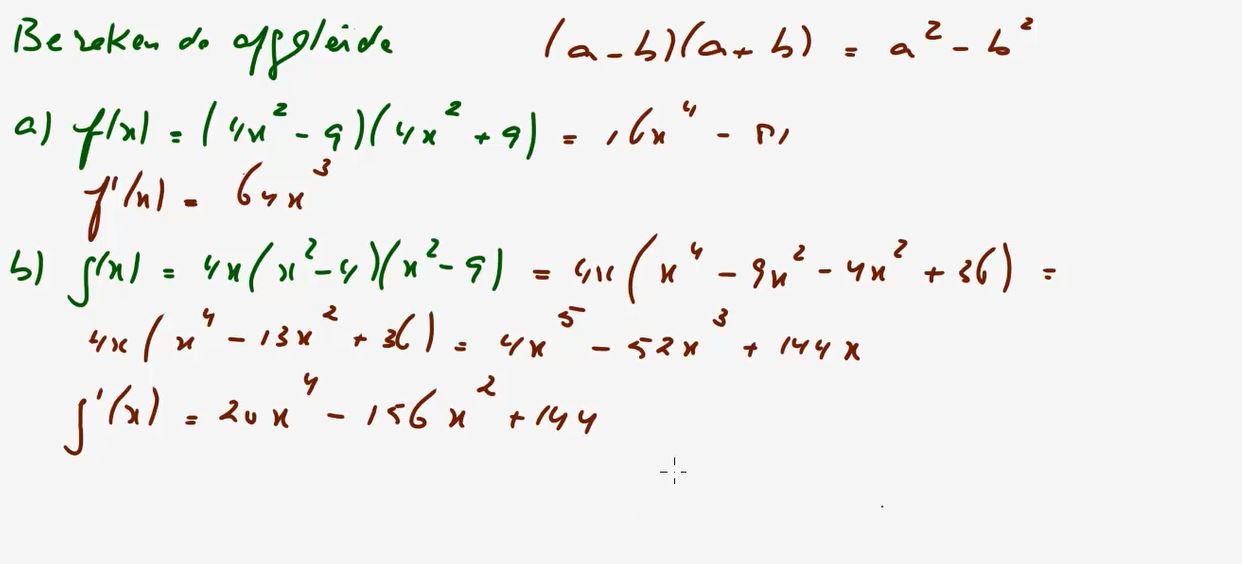Wiskunde.netLogo Wiskunde


Video uitwerking §2.5 Differentieren: opgave 82 - (2:54)

Boek: Getal & Ruimte - Veranderingen HAVO 4 (deel 1) 11e editie, 2014

Je kunt nú 1 minuut kijken. Word lid om 16.000 video-uitwerkingen in z'n geheel te bekijken. Klik hier...


Rate deze video:
Rating is 5 / 5.
Aantal stemmen: 3 keer.
Heb je een vraag of opmerking over deze video?
Laat ons weten wat je van deze video en Wiskunde.net vindt. Ben je tevreden? We horen het graag! Klik hier om je opmerking te plaatsen...
   
Opgave 73
Differentieren opgave 73 		Opgave 74
Differentieren opgave 74 		Opgave 75
Differentieren opgave 75 		Opgave 77
Differentieren opgave 77 		Opgave 78
Differentieren opgave 78 		Opgave 79
Differentieren opgave 79 		Opgave 80
Differentieren opgave 80 		Opgave 81
Differentieren opgave 81
Opgave 82
Differentieren opgave 82 		Opgave 83
Differentieren opgave 83

Differentiëren De afgeleide van f(x)=axn
×

Geel uitlegblok per bladzijde:
Blz 97: Differentiëren (13:28)
Blz 99: De afgeleide van f(x)=axn (06:44)
Andere paragrafen:
2.1. Toenamediagrammen (1 t/m 25)
2.2. Differentiequotienten en snelheden (26 t/m 45)
2.3. Raaklijnen (46 t/m 58)
2.4. Hellinggrafieken (59 t/m 72)
2.5. Differentieren (73 t/m 84)
Leerdoelen paragraaf: Differentieren:
1. De raaklijn aan de grafiek in een punt A kunnen opstellen.
2. De optie [ dy / dx ] op de grafische rekenmachine kunnen gebruiken.
3. De afgeleide van een functie kunnen bepalen.
4. De somregel van differentiëren kunnen toepassen.
5. Weten dat de afgeleide van een constante gelijk is aan 0.
6. De afgeleide van f(x) = axn kunnen berekenen.
7. De merkwaardige producten kunnen uitwerken.
Oefenen met Geogebra...

Geef je mening aan ons:
Review
Tevreden? Laat het ons weten!
Schrijf een review...
Jurgen de Bont Foto: Jurgen de Bont - Docent Wiskunde - Breda   
Welkom leerlingen op Wiskunde.net!   

Op deze site vind je duidelijke uitlegvideo's gekoppeld aan jouw boek om jou verder te helpen met het mooie vak Wiskunde. Hierboven vind je de video-uitleg van §2.5 Differentieren opgave 82 en links in het gele blokje (indien aanwezig), kun je de theorie bekijken in video. Ben je nog geen lid? Klik dan hier...
Succes verzekerd!

Met wiskundige groet,
Jurgen de Bont & Martijn Claassen & Bob Pruiksma, docenten Wiskunde onder- en bovenbouw