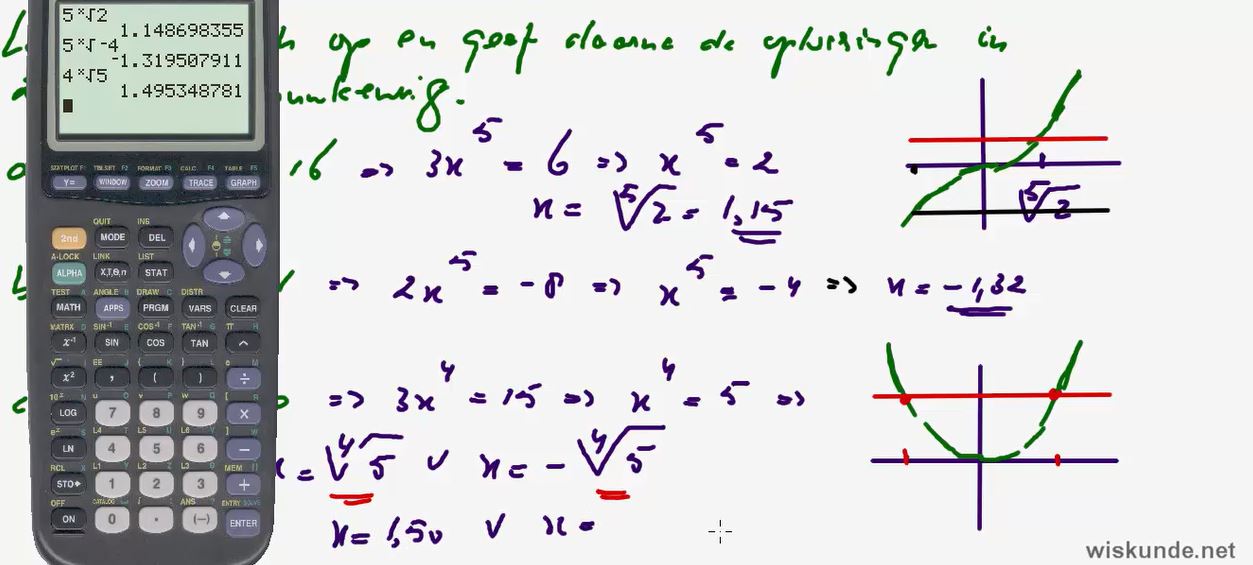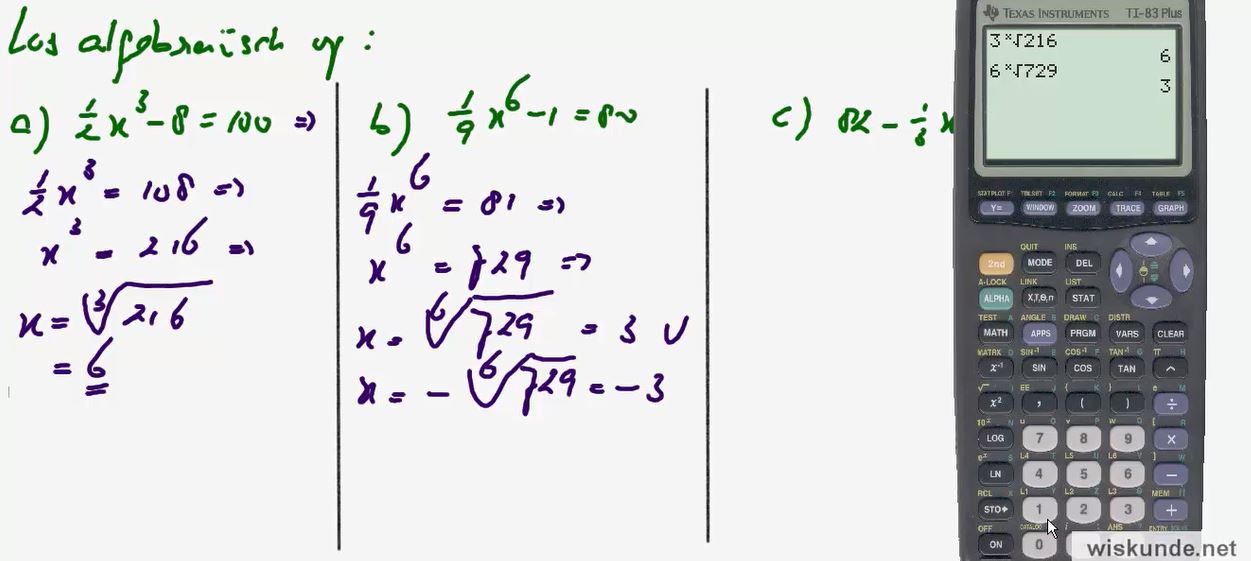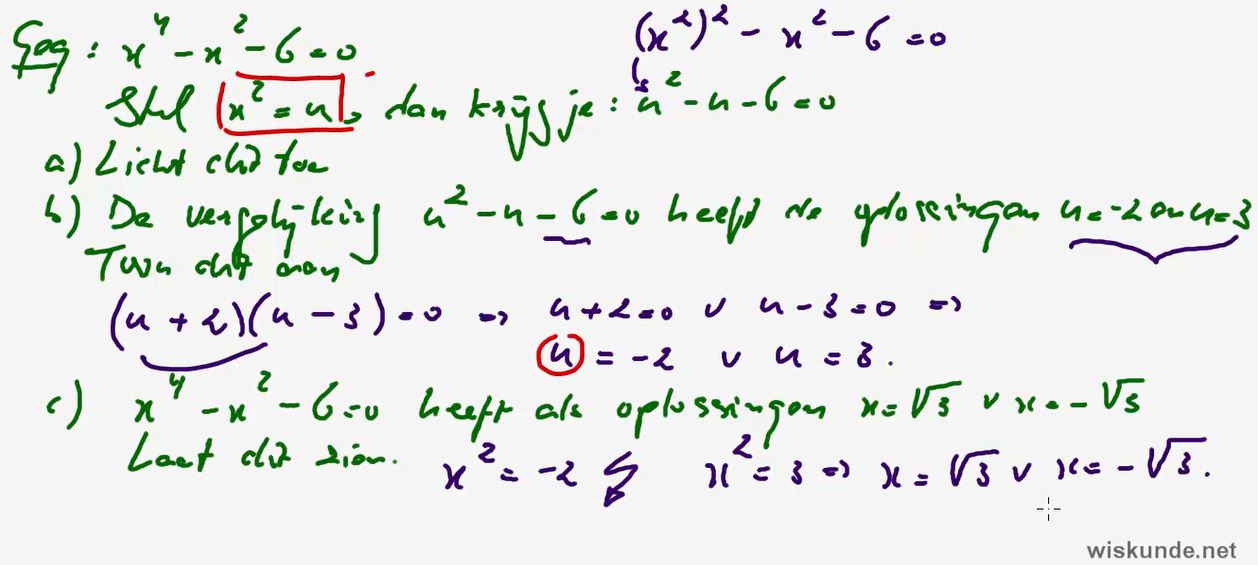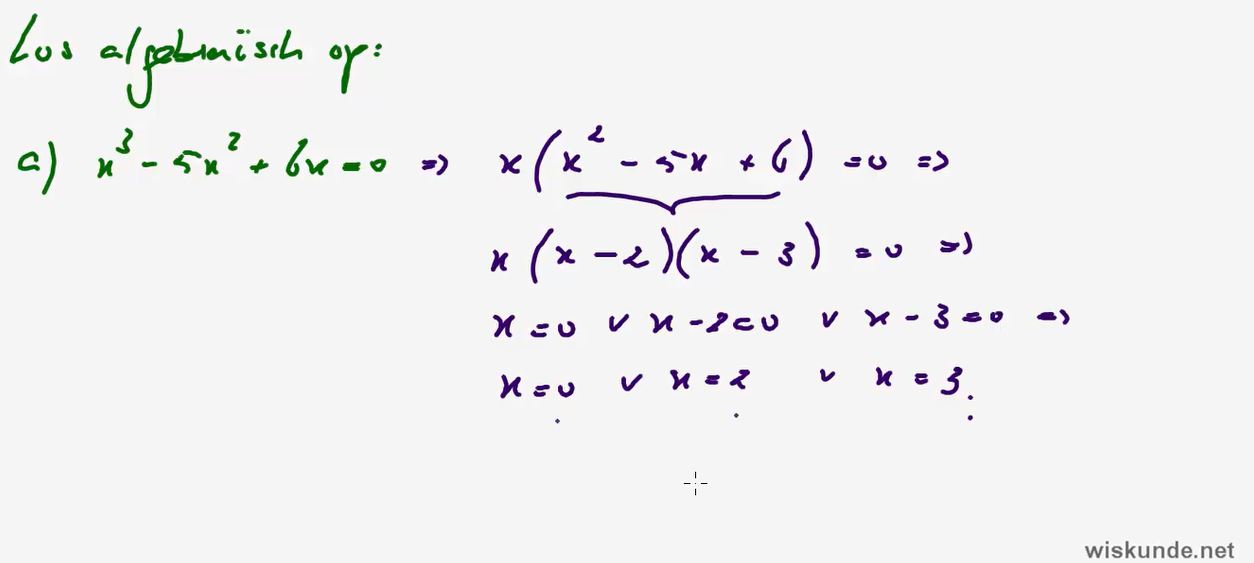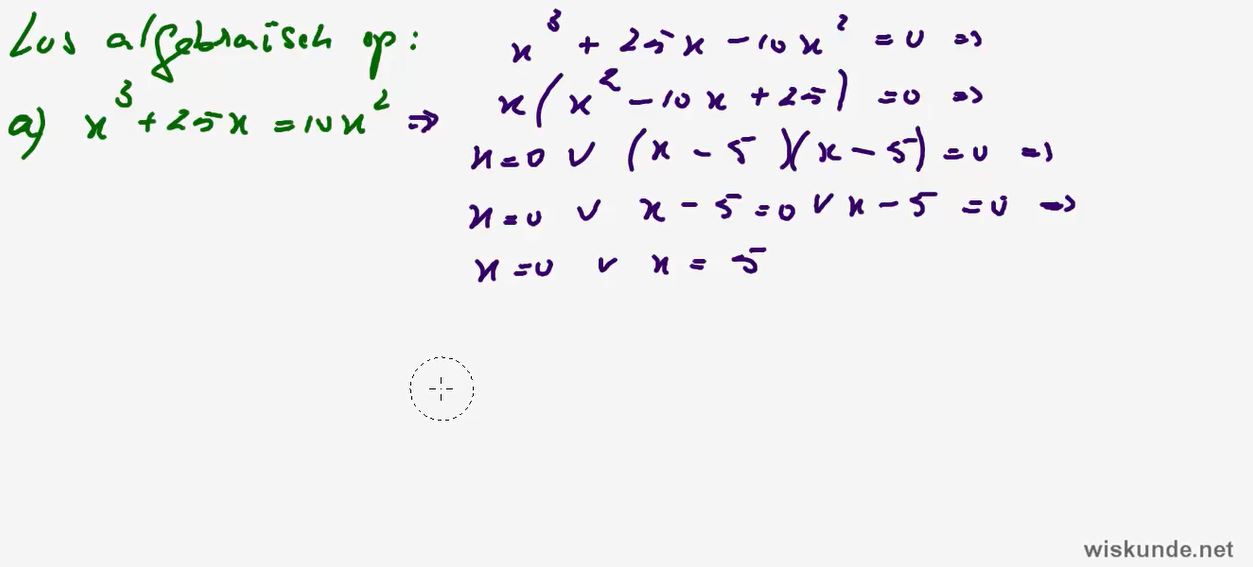Leerdoelen paragraaf: Hogeregraadsvergelijkingen:
1. Weten dat √5 ook wel de
tweedemachtswortel van 5 is.
2. Met
hogeremachtswortels kunnen rekenen.
3. De hogeremachtswortels
op je GR kunnen vinden.
4. Weten dat x
a = p, met p is even (2,4,6,..) de vorm heeft van een
olifantenpoot.
5. Weten dat x
a = p, met p is oneven (3,5,7,..) de vorm heeft van een
slang.
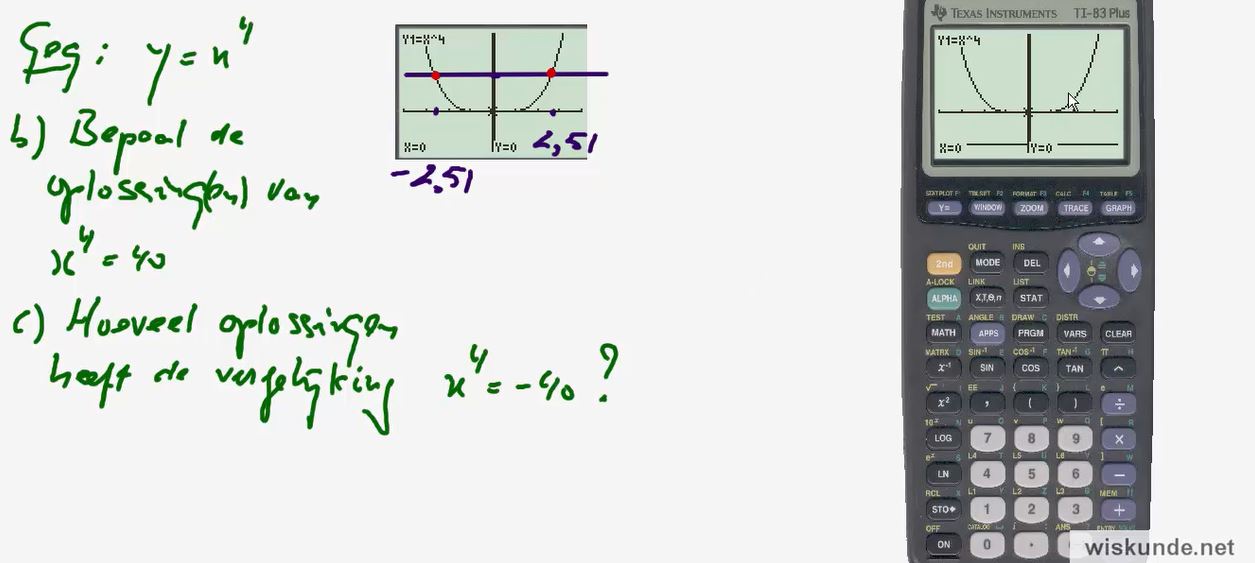
6. Inzien dat x
4 = 60
twee oplossingen heeft.
7. Inzien dat x
5 = 60
één oplossing heeft.
8. Inzien dat x
4 = -60
nul oplossingen heeft.
9. Hogeregraadsvergelijkingen algebraïsch kunnen
oplossen.
Oefenen met Geogebra...
Foto: Jurgen de Bont - Docent Wiskunde - Breda
