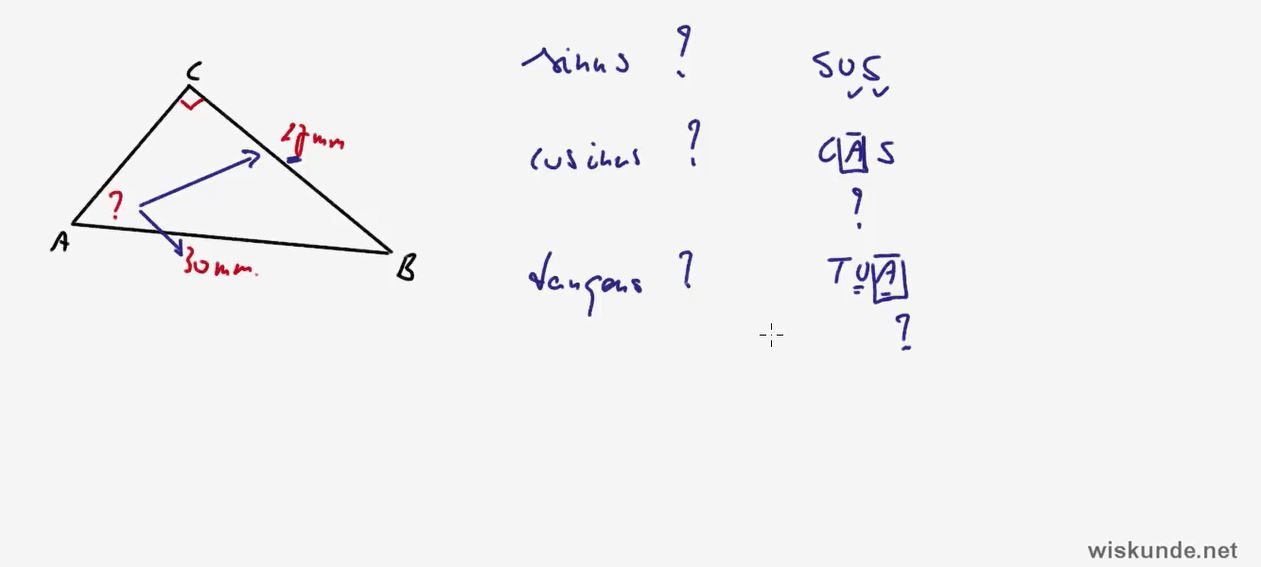
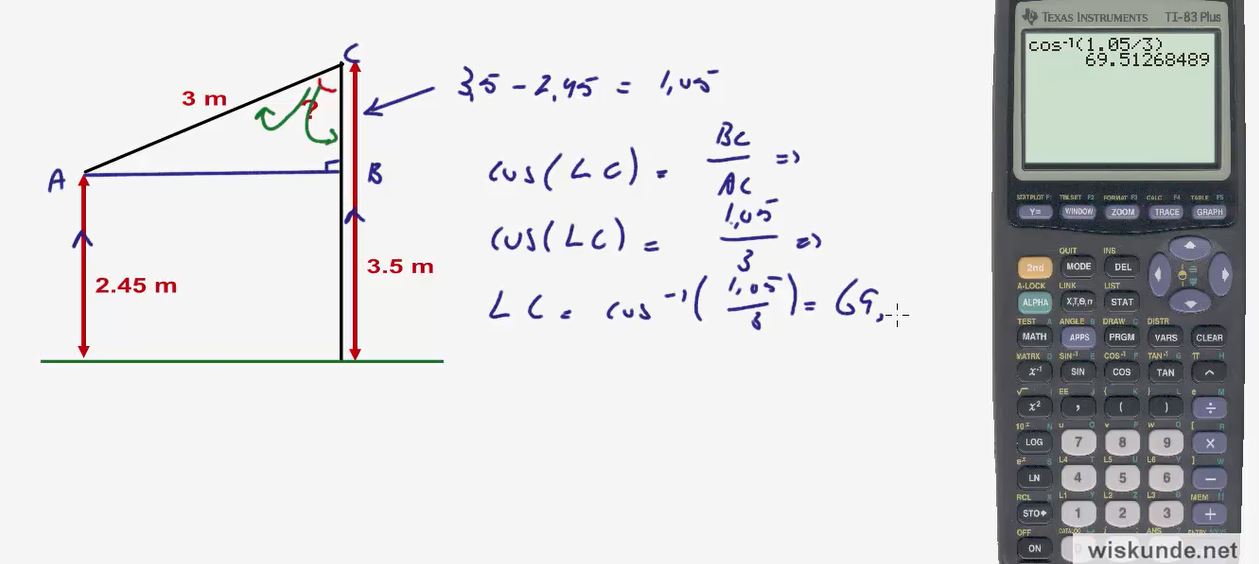
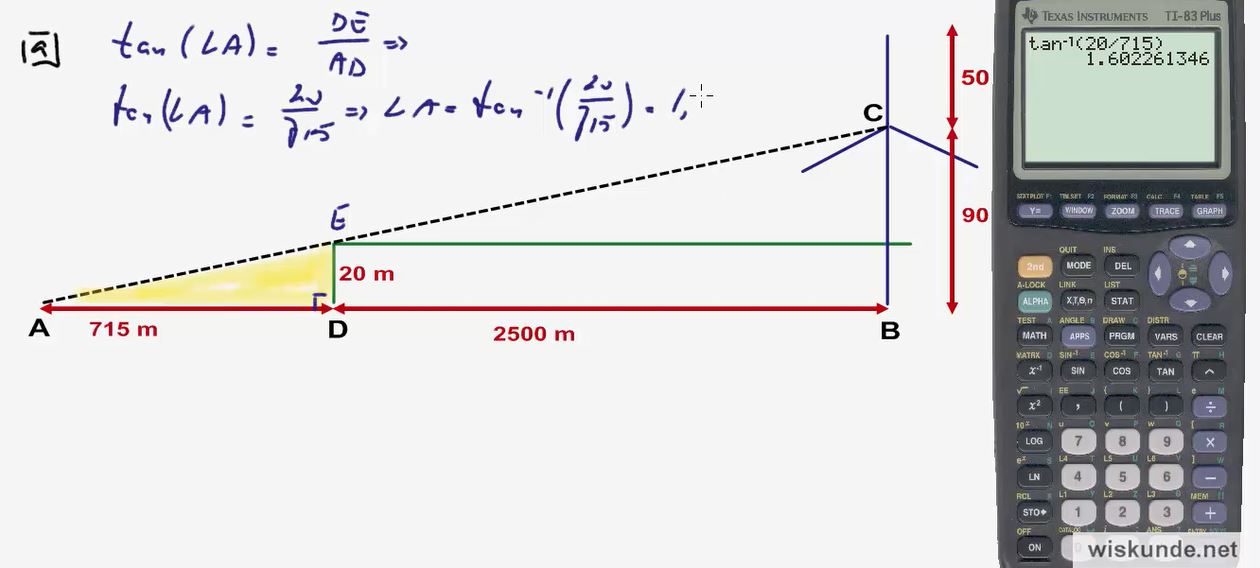
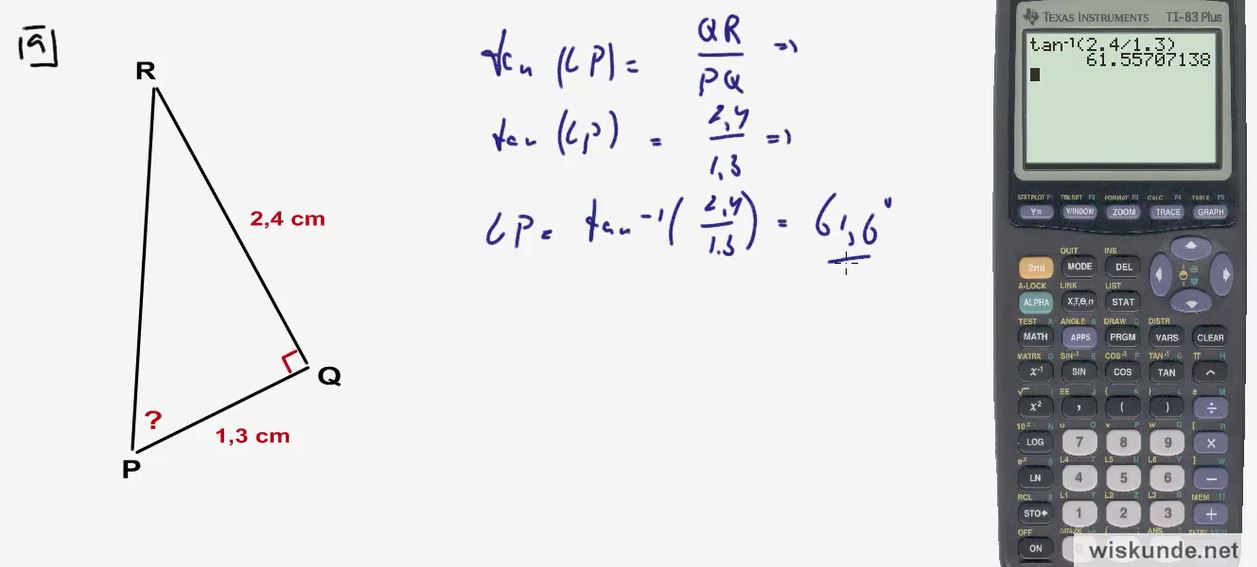Wiskunde.netLogo Wiskunde


Video uitwerking §3.2 Hoeken berekenen met goniometrie: opgave 25 - (6:27)

Boek: Getal & Ruimte - Afstanden en hoeken VMBO 4 (deel 1) 10e editie, 2016

Je kunt nú 1 minuut kijken. Word lid om 16.000 video-uitwerkingen in z'n geheel te bekijken. Klik hier...


Rate deze video:
Rating is 5 / 5.
Aantal stemmen: 1 keer.
Heb je een vraag of opmerking over deze video?
Laat ons weten wat je van deze video en Wiskunde.net vindt. Ben je tevreden? We horen het graag! Klik hier om je opmerking te plaatsen...
   
Opgave 20
Hoeken berekenen met goniometrie opgave 20 		Opgave 21
Hoeken berekenen met goniometrie opgave 21 		Opgave 22
Hoeken berekenen met goniometrie opgave 22 		Opgave 23
Hoeken berekenen met goniometrie opgave 23 		Opgave 24
Hoeken berekenen met goniometrie opgave 24 		Opgave 25
Hoeken berekenen met goniometrie opgave 25

Andere paragrafen:
3.1. Zijden berekenen (1 t/m 19)
3.2. Hoeken berekenen met goniometrie (20 t/m 25)
3.3. Hoeken in vlakke figuren (26 t/m 46)
3.4. Tekenen in perspectief (47 t/m 55)
3.5. Berekeningen in de ruimte (56 t/m 65)
3.6. Coördinaten in de ruimte (66 t/m 77)
3.7. Trainen op examenniveau (78 t/m 88)
3.8. Diagnostische toets (1 t/m 19)
Leerdoelen paragraaf: Hoeken berekenen met goniometrie:
1. De goniometrische verhoudingen kunnen benoemen.
2. Inzicht krijgen wanneer SOS CAS TOA te gebruiken.
3. De juiste keuze kunnen maken voor de SIN, COS en TAN.
4. Goniometrie kunnen toepassen in een gelijkbenige driehoek.
5. Zijden kunnen berekenen.
6. Een juiste schets kunnen maken bij de situatie.
7. Indien nodig, een hulplijn trekken bij de situatie.
Oefenen met Geogebra...

Geef je mening aan ons:
Review
Tevreden? Laat het ons weten!
Schrijf een review...
Jurgen de Bont Foto: Jurgen de Bont - Docent Wiskunde - Breda   
Welkom leerlingen op Wiskunde.net!   

Op deze site vind je duidelijke uitlegvideo's gekoppeld aan jouw boek om jou verder te helpen met het mooie vak Wiskunde. Hierboven vind je de video-uitleg van §3.2 Hoeken berekenen met goniometrie opgave 25 en links in het gele blokje (indien aanwezig), kun je de theorie bekijken in video. Ben je nog geen lid? Klik dan hier...
Succes verzekerd!

Met wiskundige groet,
Jurgen de Bont & Martijn Claassen & Bob Pruiksma, docenten Wiskunde onder- en bovenbouw