Uitwerking 6.2 Het berekenen van schuine zijden opgave 18
01-07-2025
admin
Getal & Ruimte HAVO/VWO 2 (deel 2) hoofdstuk 6 De stelling van Pythagoras
Uitleg
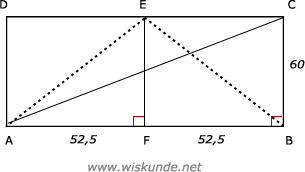
De punten A, B en C vormen een rechthoekige driehoek. Maak een schets van een driehoek. De rechthoekszijden zijn AB = 106 meter en BC = 60 meter. AC is dus de schuine. Deze is te berekenen met de Stelling van Pythagoras. Bij opgave b. krijg je 2 driehoeken met schuine zijden BE en AE.
Vraag 18
Gegeven een voetbalveld van 105 meter bij 60 meter. De spelers rennen via A, B en C weer terug naar A.
a. Hoeveel meter lopen ze?
b. Hoeveel lopen ze als ze ABEA lopen?
Antwoord
a.
AB(kwadraat) + BC(kwadraat) = AC(kwadraat)
105(kwadraat) + 60(kwadraat) = AC(kwadraat)
AC(kwadraat) = 14625
AC = (wortel)14625
AC (ongeveer) 120,93 meter.
AB + BC + AC = 105 + 60 + 120,93 = 285,93 meter.
b.
AF(kwadraat) + EF(kwadraat) = AE(kwadraat)
52,5(kwadraat) + 60(kwadraat) = AE(kwadraat)
AE(kwadraat) = 6356,25
AE = (wortel)6356,25
AE (ongeveer) 79,73 meter.
AB + BE + AE = 105 + 79,73 + 79,73 = 264,46 meter.
Uitwerking
Wil je meer uitleg over: Reageer op deze uitwerking
Heb je een vraag over deze opgave, snap je iets niet of ben je een fout tegengekomen en wil je binnen 10 minuten antwoord? Stel een vraag!