Stelling van Pythagoras
 01-01-2026
01-01-2026 admin
admin 23
23
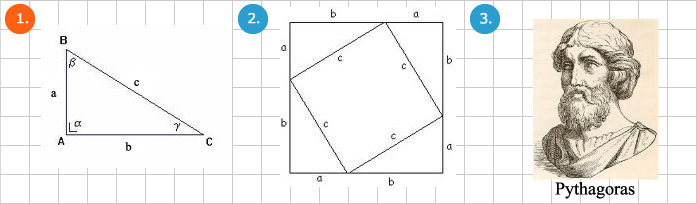
Inleiding
De stelling van Pythagoras is een van de bekendste wiskundige formules en een van de weinige die mensen na school onthouden. De stelling kent ook veel dagelijkse toepassingen. Dit betekent dat steeds twee van de lengten a, b en c bepalend zijn voor de derde. Wanneer bijvoorbeeld de korte zijden van een rechthoekige driehoek de lengten 3 en 4 hebben, geldt: c2 = 32 + 42 = 25, dus c = 5. De stelling geldt voor alle rechthoekige driehoeken, ongeacht of de lengten van de zijden een heel, een rationeel of irrationeel getal is. De stelling van Pythagoras stelt dat bij een rechtloekige driehoek de som van de kwadraten van de twee korte zijden gelijk is aan het kwadraat van de lange zijde. Als formule: a2 + b2 = c2
In de bouw wordt de stelling van Pythagoras gebruikt om te controleren hoe recht een hoek is. Ik betwijfel echter of de bouwvakkers zeggen 'Wacht even... ik pas eerst de Stelling van Pythagoras even toe op deze hoek'. Maar ze gebruiken hem wel degelijk, want om er snel achter te komen of een hoek recht is (90 graden), meet je langs één muur drie meter af, langs de andere vier meter en meet je vervolgens de diagonaal tussen die twee punten. Als de diagonaal niet vijf meter is, is de hoek niet recht. Je kunt ook veelvouden van drie en vier langs beide muren afmeten voor een grotere nauwkeurigheid.
Formule Stelling van Pythagoras
Voorbeelden Stelling van Pythagoras
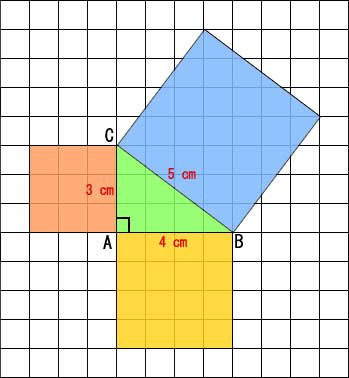
Voorbeeld 1
Gegeven een rechthoekige driehoek met hoekpunten A, B en C. Hoek A is een rechte hoek. Lijnstuk AB = 4 cm en lijnstuk AC = 3 cm.
Bereken de lengte van BC. We noemen BC de schuine zijde of hypotenusa.
Uitwerking:
Gebruik de formule: a2 + b2 = c2.
In plat Nederlands: de ene rechthoekszijde2 + de andere rechthoekszijde2 = schuine 2.
Dit levert: AB2 + AC2 = BC2.
Vul in wat je weet: 42 + 32 = BC2.
Hieruit volgt dat BC2 = 25 => BC = √25 => BC = 5.
Bewijs Stelling van Pythagoras
Dit is een van de vele manieren waarop de Stelling kan worden bewezen (zie afb.2). De oppervlakte van het grote vierkant is:
(a+b)2 of (a+b)(a+b)
Na vermenigvuldiging en de verzameling van soortgelijke termen, wordt dit: a2+2ab+b2.
De oppervlakte van het grote vierkant kan ook worden bepaald door de oppervlakten van de vier driehoeken en het kleine vierkant met zijden van lengte c bij elkaar op te tellen.
De oppervlakte van het scheve vierkant is c2 en de oppervlakte van elk van de driehoeken is 1/2ab. De som van de vier driehoeken en het scheve vierkant is:
4 * 1/2ab + c2
Dit komt neer op 2ab + c2. Omdat we het over hetzelfde vierkant hebben, moeten de oppervlakten gelijk zijn. Dus:
a2 + 2ab + b2 = 2ab + c2
De 2ab aan beide kanten van de vergelijking kunnen tegen elkaar worden weggestreept:
a2 + b2 = c2
Extra
Hoewel de formule naar Pythagoras is vernoemd, was de stelling al lang voor zijn tijd bekend bij de Babyloniërs en Indiërs.
Maar Pythagoras, of misschien een van de pythagoreeërs, was waarschijnlijk de eerste die de stelling heeft bewezen.
De stelling van Pythagoras is de stelling met de meeste bewijzen: tot op heden zijn er ongeveer 400 bewijzen bekend, waaronder ook een bewijs dat werd geleverd door de Amerikaanse president J.A. Garfield (1831- 1881).
Pythagorisch drietallen
In het voorbeeld hierboven waarin drie, vier en vijf worden gebruikt voor de zijden van een rechthoekige driehoek, heet een 'pythagorisch drietal'.
Er zijn veel pythagorische drietallen, waaronder alle veelvouden van drie, vier en vijf.
In feite maken de beeldverhoudingen (de hoogte-breedteverhouding) van normale (4:3) en breedbeeld (16:9) televisies deel uit van pythagorische drietallen.
Hier is de formule om deze te bepalen. Gegeven zijn twee hele getallen n en m waarbij n groter is dan m:
a = n2 - m2
b = 2 * n * m
c = n2 + m2
Dus als n=2 en m=1 dan:
a = 3, b = 4, c = 5
3D: Pythagoras in de ruimte
Nog iets interessants van de Stelling van Pythagoras is dat deze kan worden toegepast op andere dimensies.
Voor ons, in de echte wereld, betekent dat drie dimensies. Stel bijvoorbeeld dat een meisje prulletjes verzamelt en een schoenendoos wil gebruiken om die in te bewaren.
Ze ziet een mooi potlood in de winkel, maar voordat ze het koopt, wil ze weten of dit in de doos past. Ieder ander had het potlood gewoon gekocht, maar dit meisje is erg precies.
Gelukkig kent ze de afmetingen van de doos: die is 18 cm breed, 28 cm lang en 11 cm hoog. Dan past ze de stelling toe op drie dimensies, ofwel:
a2 + b2 + c2 = d2
waarbij a,b en c de breedte, lengte en hoogte zijn en d de diagonaal is. Nu krijg ze:
182 + 282 + 112 = d2
Dit wordt: 324 + 784 + 121 = d2 ofwel d2 = 1129. Als we de wortel uit beide kanten nemen, zien we dat een potlood van 35 cm erin past.
Gerelateerd
Oppervlakte trapezium Wat is een trapezium? Een trapezium is een vierhoek waarvan minstens 1 paar over...
Inhoud prisma Een prisma is een meetkundig figuur dat bestaat uit allemaal rechthoeken, behalv...
Video's
Word ook lid!
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


