Uitwerking 6.4 Pythagoras in de ruimte opgave 46
01-07-2025
admin
Getal & Ruimte HAVO/VWO 2 (deel 2) hoofdstuk 6 De stelling van Pythagoras
Uitleg
Noem de linkerdraad l. Noem de rechterdraad r en noem de diagonaal van het dak d (ligt dus op het grondvlak van het dak). Stel de middelste draad m.
Vraag 46
Op een dak staat een vlaggenmast. Deze heeft een hoogte van 6 meter. De mast is verbonden met draden aan de hoekpunten van het dak. Bereken de lengte van de draden in meters. De mast staat in een hoekpunt.
Antwoord
6(kwadraat) + 4(kwadraat) = d1(kwadraat)
d1(kwadraat) = 36 + 16
d1(kwadraat) = 52
d1 = (wortel)52
d1 (ongeveer) 7,21 m (draad links)
8(kwadraat) + 4(kwadraat) = d3(kwadraat)
d3(kwadraat) = 64 + 16
d3(kwadraat) = 80
d3 = (wortel)80
d3 (ongeveer) 8,94 m (draad rechts)
Nu de middelste draad d2:
AB(kwadraat) + AD(kwadraat) = BD(kwadraat)
8(kwadraat) + 6(kwadraat) = BD(kwadraat)
BD(kwadraat) = 64 + 36
BD(kwadraat) = 100
BD = (wortel)100
BD = 10 m
BD(kwadraat) + DE(kwadraat) = BE(kwadraat)
10(kwadraat) + 4(kwadraat) = BE(kwadraat)
BE(kwadraat) = 100 + 16
BE(kwadraat) = 116
BE = (wortel)116
BE (ongeveer) 10,77 m (draad midden = d2)
Totale lengte van de draad is: d1 + d2 + d3 = (wortel)52 + (wortel)116 + (wortel)80 = 26,93 meter.
Uitwerking
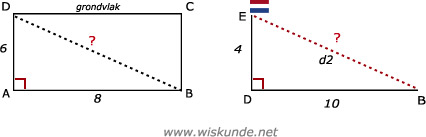
Voor de draad links (l) geldt:
62 + 42 = l2
36 + 16 = l2
l2 = 52
Hieruit volgt dat: l = √52
Voor de diagonaal d op het dak (grondvlak) geldt:
82 + 62 = d2
64 + 36 = d2
d2 = 100
Hieruit volgt dat: d = √100 = 10
Voor de middendraad m (lichaamsdiagonaal) geldt:
d2 + 42 = m2
100 + 16 = m2
m2 = 116
Hieruit volgt dat: m = √116
Voor de draad rechts (r) geldt:
82 + 42 = r2
64 + 16 = r2
r2 = 80
Hieruit volgt dat: r = √80
Tellen we nu de lengte van alle draden op dan krijgen we: √52 + √116 + √80 ≈ 26,93 meter.
Reageer op deze uitwerking
Heb je een vraag over deze opgave, snap je iets niet of ben je een fout tegengekomen en wil je binnen 10 minuten antwoord? Stel een vraag!