Uitwerking 6.4 Pythagoras in de ruimte opgave 47
01-07-2025
admin
Getal & Ruimte HAVO/VWO 2 (deel 2) hoofdstuk 6 De stelling van Pythagoras
Uitleg
Nu hoeven we dus niet "een" lichaamsdiagonaal te berekenen. Deze is nu namelijk gegeven. Dat is de lengte van de pen. Maar bereken de hoogte a bij een gegeven lichaamsdiagonaal. Bereken eerst de lengte van de diagonaal in het grondvlak. Bereken daarna a in het verticale diagonaalvlak.
Vraag 47
Gegeven een pennenbakje van glas. Deze heeft de vorm van een kubus. De ribben zijn 10 cm. In de kubus ligt een pen. De pen heeft een lengte van 16,5 cm. Bereken de hoogte van a.
Antwoord
AB(kwadraat) + BC(kwadraat) = AC(kwadraat)
10(kwadraat) + 10(kwadraat) = AC(kwadraat)
AC(kwadraat) = 100 + 100
AC(kwadraat) = 200
AC = (wortel)200
AC (ongeveer) 14,14
Bereken nu AX (=a) in driehoek ACX:
AC(kwadraat) + AX(kwadraat) = CX(kwadraat)
200 + AX(kwadraat) = 16,5(kwadraat)
AX(kwadraat) = 16,5(kwadraat) - 200
AX(kwadraat) = 72,25
AX = (wortel)72,25
AX = 8,5 cm
Dus de hoogte van a is 8,5 cm.
Uitwerking
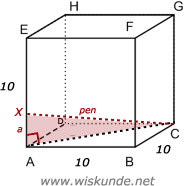
Maak eerst een schets van het grondvlak. Teken daarin de diagonaal d. Deze d berekenen we als volgt:
102 + 102 = d2
100 + 100 = d2
d2 = 200
Hieruit volgt dat: d = √200
Schets nu een nieuwe rechthoekige driehoek met d als "bodem" en de pen als schuine zijde (16,5 cm). We krijgen dan:
d2 + a2 = 16,52
200 + a2 = 272,25
Links en rechts -200 (balansmethode) levert:
a2 = 72,25
Hieruit volgt dat: a = √72,25 = 8,5 cm
Reageer op deze uitwerking
Heb je een vraag over deze opgave, snap je iets niet of ben je een fout tegengekomen en wil je binnen 10 minuten antwoord? Stel een vraag!