Wiskunde.net

a.
x = 20 invullen, levert: h = -0,03 ⋅ (20)(kwadraat) + 1,5 ⋅ 20 = -0,03 ⋅ 400 + 30 = -12 + 30 = 18 (meter)
x = 30 invullen, levert: h = -0,03 ⋅ (30)(kwadraat) + 1,5 ⋅ 30 = -0,03 ⋅ 900 + 45 = -27 + 45 = 18 (meter)
b.
X_top ligt in het midden van x = 20 en x = 30. Dus X_top = 25.
x = 25 invullen, levert: h = -0,03 ⋅ (25)(kwadraat) + 1,5 ⋅ 25 = -0,03 ⋅ 625 + 37,5 = -18,75 + 37,5 = 18,75 (meter)
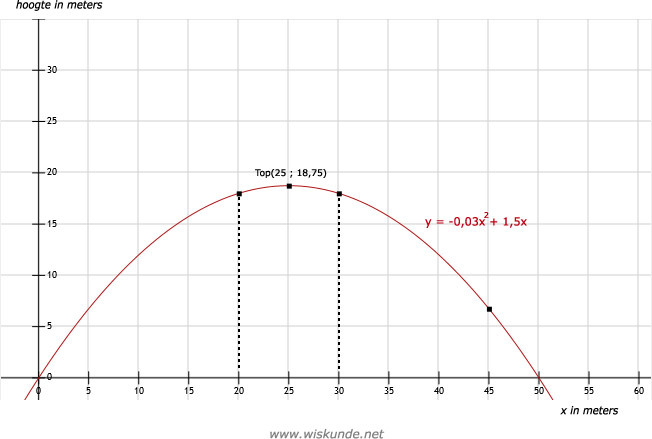
Dus de maximale hoogte is 18,75 meter bij x = 25 meter (top van de parabool: (25 ; 18,75)).
c.
x = 18 invullen, levert: h = -0,03 ⋅ (18)(kwadraat) + 1,5 ⋅ 18 = 17,28 (meter)
x = 10 invullen, levert: h = -0,03 ⋅ (10)(kwadraat) + 1,5 ⋅ 10 = 12 (meter)
Het verschil is dus 17,28 - 12 = 5,28 meter.
d.
x = 45 invullen, levert: h = -0,03 ⋅ (45)(kwadraat) + 1,5 ⋅ 45 = -0,03 ⋅ 2025 + 67,5 = -60,75 + 67,5 = 6,75 (meter)
Dus bij x = 45 is de hoogte nog 6,75 meter. Dus de bal is bij een grotere x pas op de grond (zie x = 50).
Dus hij trapt de bal verder weg dan 45 meter.