Leerdoelen paragraaf: Kwadratische formules:
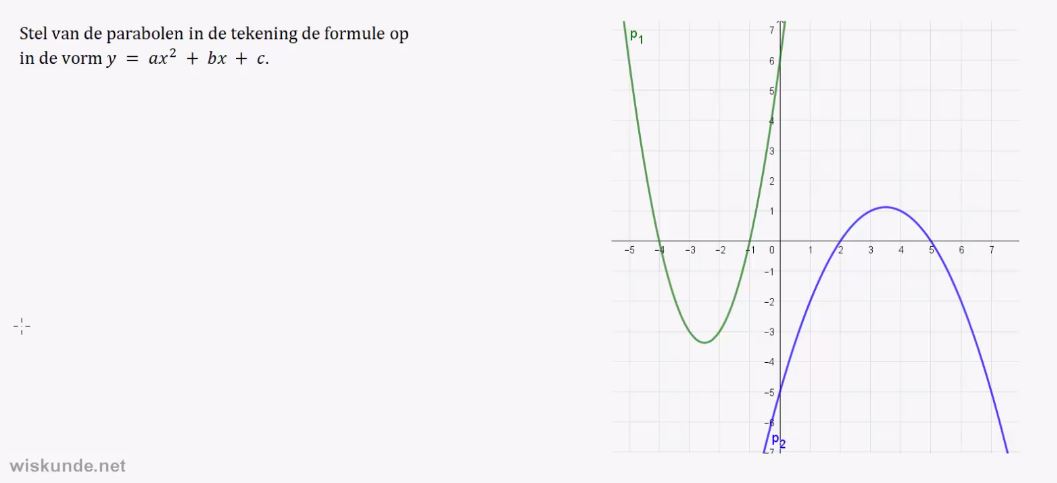
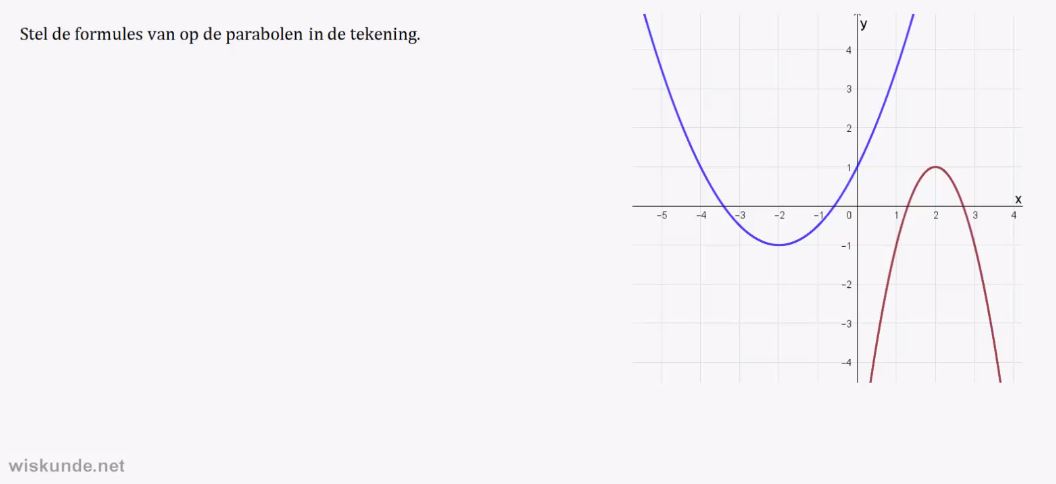
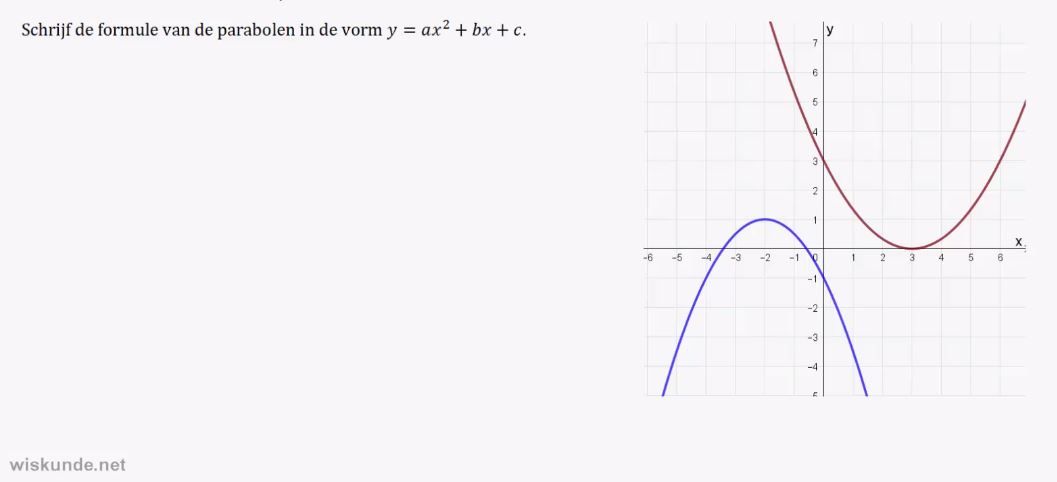
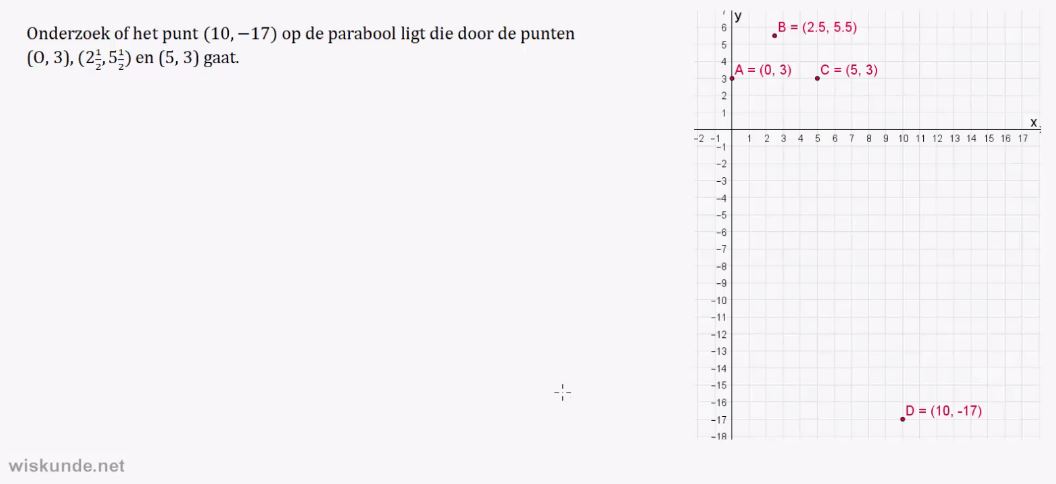
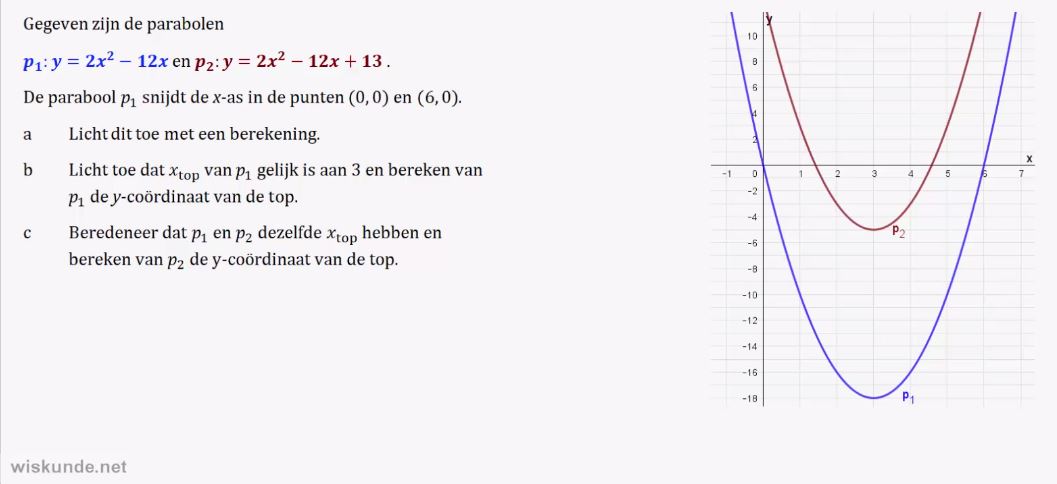
1. Parabool van de vorm:.
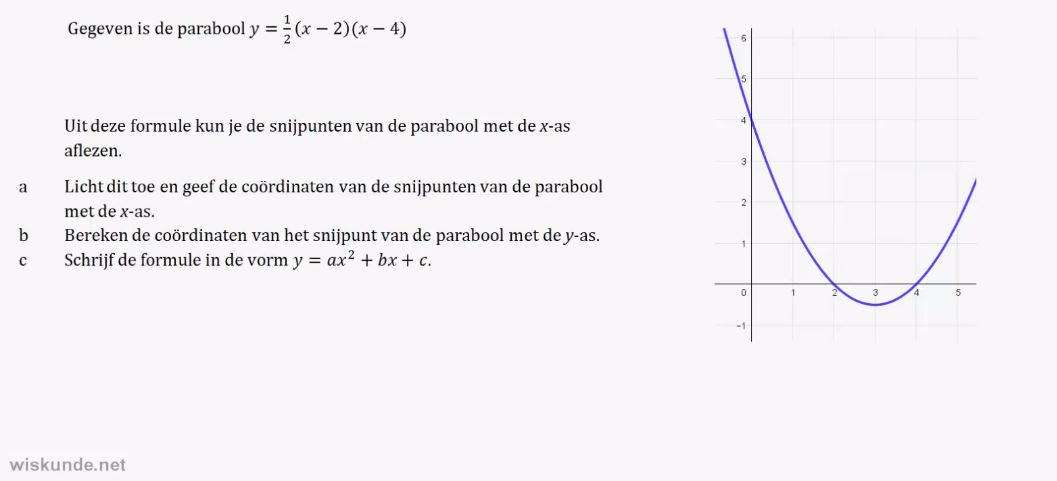
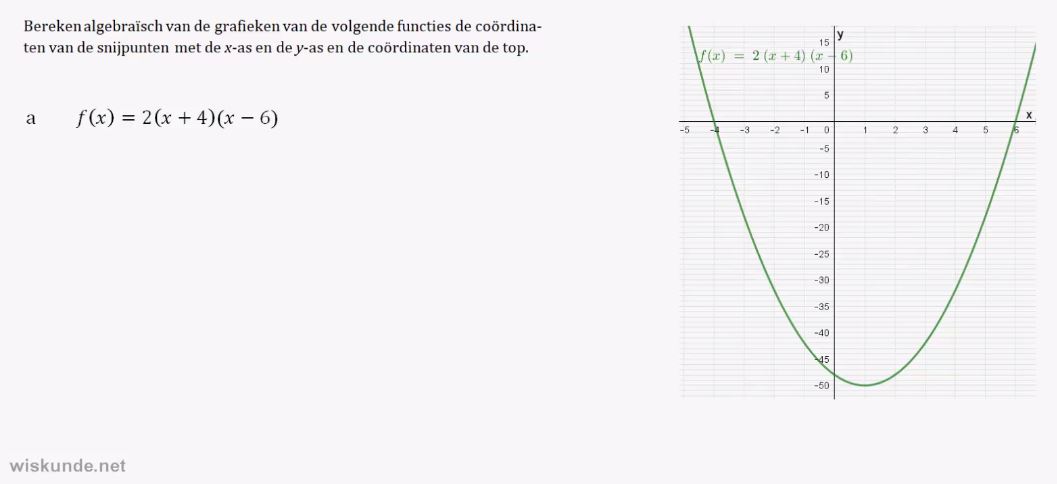
y = a(x – d)(x – e) herkennen.
2. Snijpunten met de x-as kunnen opschrijven van de parabool y = a(x – d)(x – e).
3. De parabool van de vorm
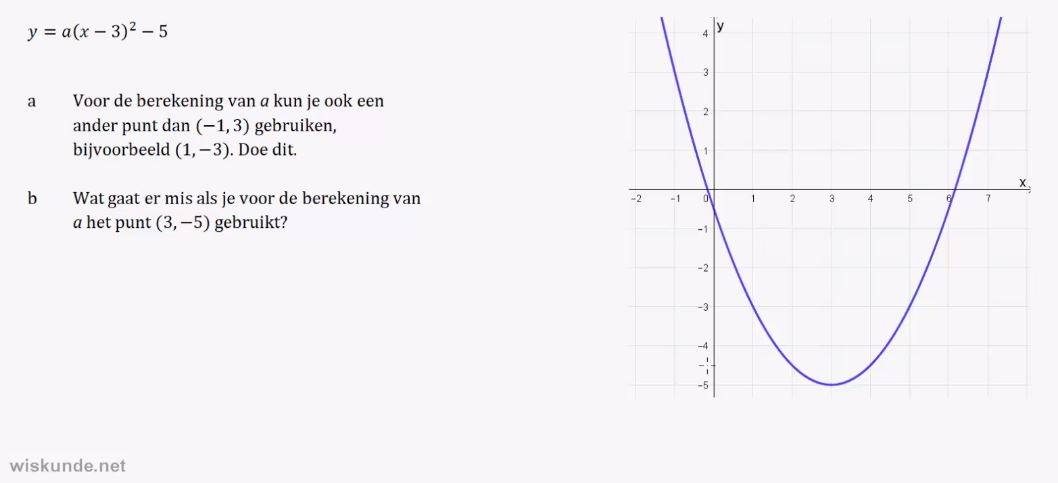
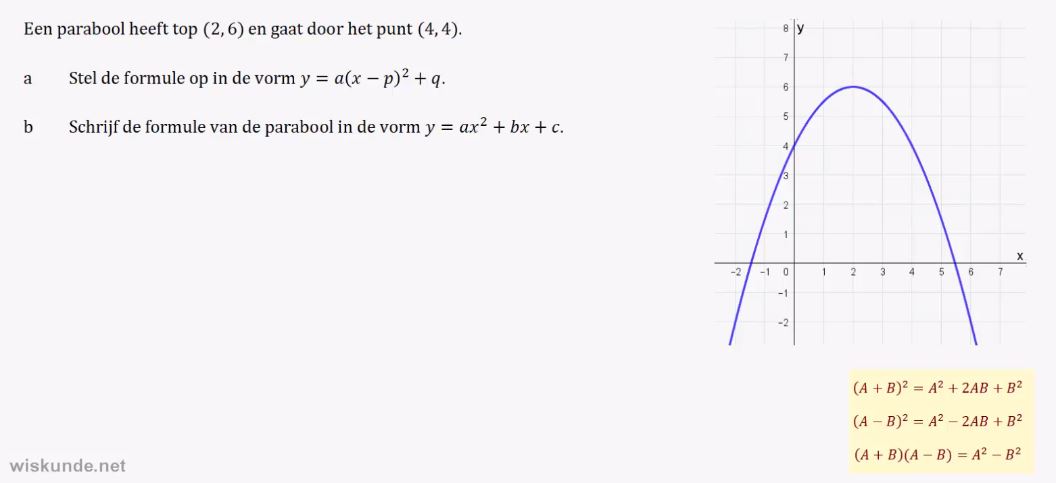
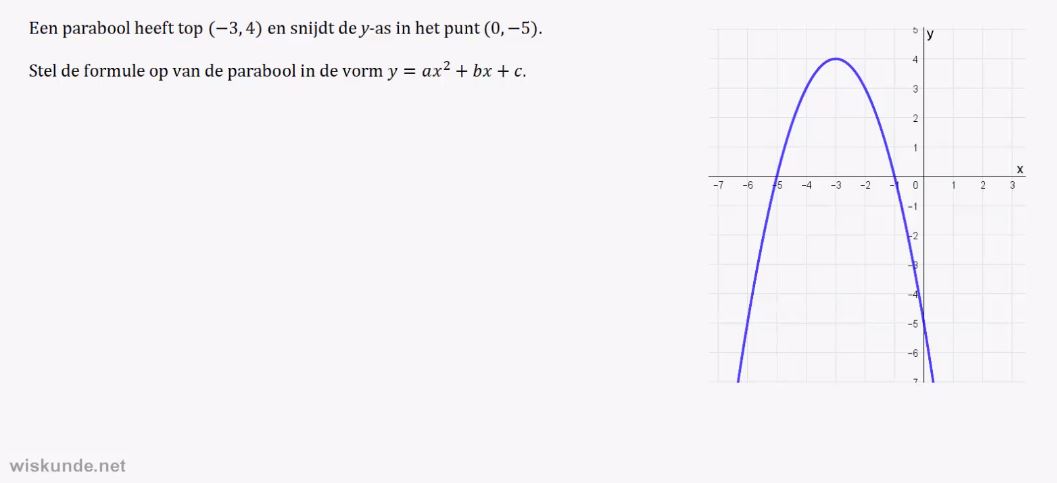
y = a(x - p)2 + q herkennen.
4. De top van de parabool y = a(x - p)
2 + q in
1 keer kunnen opschrijven.
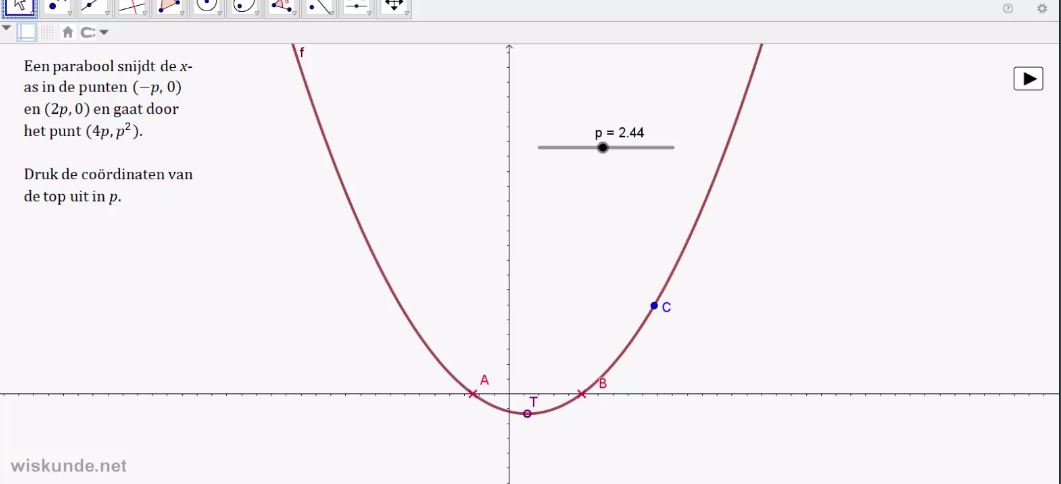
5. De
Xtop en Ytop kunnen berekenen van de Top van de parabool.
6. Weten dat de Y
top gelijk is aan de
f(Xtop). Dus de X
top invullen in de functie/formule.
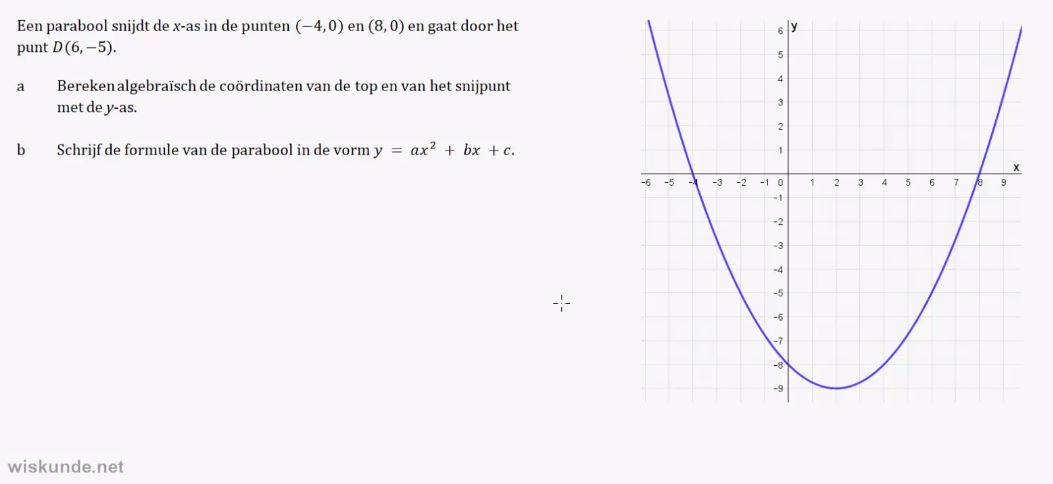
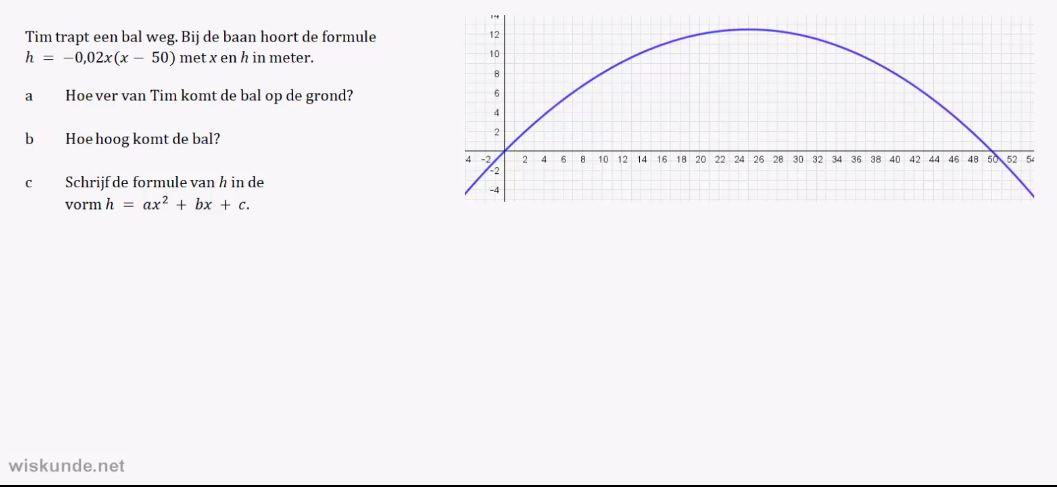
7. Snijpunten van een parabool met de
x-as en y-as berekenen.
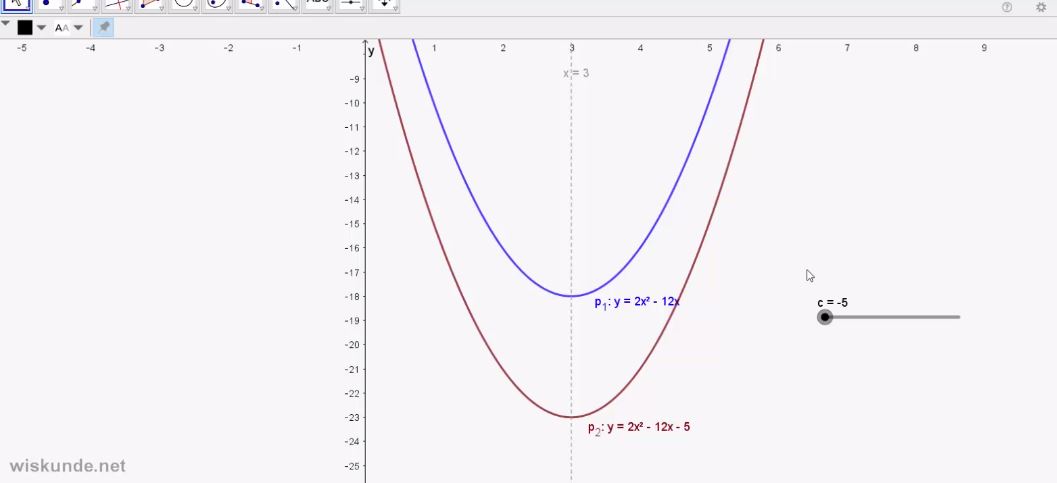
Oefenen met Geogebra...
