TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 9.4 Tellen met en zonder herhaling VWO 3
Boek: Getal & Ruimte - Statistiek VWO 3 (deel 2) opgaven 35 t/m 55, 2011Wat is de vermenigvuldigingsregel?
De vermenigvuldigingsregel gebruik je als handeling I op p manieren kan en handeling II op q manieren kan en handeling III op r manieren kan.
De gecombineerde handeling kun je dan op p x q x r manieren doen.
De vermenigvuldigingsregel gebruik je als handeling I op p manieren kan en handeling II op q manieren kan en handeling III op r manieren kan.
De gecombineerde handeling kun je dan op p x q x r manieren doen.
35.
a. Aantal mogelijke combinaties: 3 x 2 x 3 = 18
b. Aantal mogelijke combinaties: 1 x 2 x 3 = 6
c. Aantal mogelijke combinaties: 3 x 1 x 1 = 3
36.
b. Aantal mogelijke combinaties: 4 x 5 x 4 x 2 = 160
c. Aantal mogelijke combinaties: 3 x 5 x 4 x 3 = 180
d. Aantal mogelijke combinaties: 4 x 5 x 1 x 1 = 20
e. Aantal mogelijke combinaties: 1 x 3 x 4 x 3 = 36
37.
b. Aantal mogelijke combinaties: 1 x 3 x 6 = 18
c. Aantal mogelijke combinaties: 3 x 4 x 6 = 72
d. Aantal mogelijke combinaties: 3 x 2 x 3 = 18
e. Aantal mogelijke combinaties: 5 x 4 x 1 = 20
38.
a. Op 600 manieren kan hij een band samenstellen.
b. 1280 - 600 levert een toename van 680.
39.
a. Aantal mogelijke combinaties: 12 x 17 = 204
b. Aantal mogelijke combinaties: 10 x 6 = 60
c. Aantal mogelijke combinaties: 4 x 3 = 12
d. Aantal mogelijke combinaties: 7 x 14 = 98
40.
a. Aantal mogelijke combinaties: 1 x 6 x 2 = 12
b. Aantal mogelijke combinaties: 2 x 1 x 3 = 6
c. Aantal mogelijke combinaties: 6 x 6 x 3 = 108
d. Aantal mogelijke combinaties: 6 x 10 x 10 = 600
41.
a. Aantal mogelijke combinaties: 24 x 24 = 576
b. Aantal mogelijke combinaties: 24 x 23 = 552
c. Kies methode 2. Bij methode 1 loop je de kans dat 1 persoon 2x wint. Dat is minder eerlijk.
42.
b. 7 x 7 x 7 x 7 = 2401
c. 1 x 1 x 7 x 7 = 49
d. 1 x 1 x 5 x 4 = 20
43.
a. 10 x 10 x 10 x 10 = 10 000
b. 10 x 9 x 8 x 7 = 5040
c. 10 x 1 x 1 x 1 = 10
d. 5 x 5 x 5 x 5 = 625
44.
Met herhaling: 7 x 7 x 7 x 7 = 2401
b. 5-lettercode MET herhaling: 7 x 7 x 7 x 7 x 7 = 16 807
5-lettercode ZONDER herhaling: 7 x 6 x 5 x 4 x 3 = 2520
Het verschil is inderdaad groter dan 14 000.
a. Aantal mogelijke combinaties: 3 x 2 x 3 = 18
b. Aantal mogelijke combinaties: 1 x 2 x 3 = 6
c. Aantal mogelijke combinaties: 3 x 1 x 1 = 3
36.
Tip:
Alleen even getallen? Dat betekent dat de 1e 3 schijven alles kunnen zijn, alleen de laatste schijf mag dan alleen een 4 of een 6 zijn.
a. Aantal mogelijke combinaties: 4 x 5 x 4 x 3 = 240Alleen even getallen? Dat betekent dat de 1e 3 schijven alles kunnen zijn, alleen de laatste schijf mag dan alleen een 4 of een 6 zijn.
b. Aantal mogelijke combinaties: 4 x 5 x 4 x 2 = 160
c. Aantal mogelijke combinaties: 3 x 5 x 4 x 3 = 180
d. Aantal mogelijke combinaties: 4 x 5 x 1 x 1 = 20
e. Aantal mogelijke combinaties: 1 x 3 x 4 x 3 = 36
37.
Tip:
Groter dan 520? Dan kan schijf 1 nog maar een 5 zijn, schijf 2 nog maar 2, 3 en 4 en schijf 3 kan nog alles zijn. Dat levert 1 x 3 x 6 = 18 combinaties.
a. Aantal mogelijke combinaties: 5 x 4 x 6 = 120Groter dan 520? Dan kan schijf 1 nog maar een 5 zijn, schijf 2 nog maar 2, 3 en 4 en schijf 3 kan nog alles zijn. Dat levert 1 x 3 x 6 = 18 combinaties.
b. Aantal mogelijke combinaties: 1 x 3 x 6 = 18
c. Aantal mogelijke combinaties: 3 x 4 x 6 = 72
d. Aantal mogelijke combinaties: 3 x 2 x 3 = 18
e. Aantal mogelijke combinaties: 5 x 4 x 1 = 20
38.
a. Op 600 manieren kan hij een band samenstellen.
b. 1280 - 600 levert een toename van 680.
39.
a. Aantal mogelijke combinaties: 12 x 17 = 204
b. Aantal mogelijke combinaties: 10 x 6 = 60
c. Aantal mogelijke combinaties: 4 x 3 = 12
d. Aantal mogelijke combinaties: 7 x 14 = 98
40.
a. Aantal mogelijke combinaties: 1 x 6 x 2 = 12
b. Aantal mogelijke combinaties: 2 x 1 x 3 = 6
c. Aantal mogelijke combinaties: 6 x 6 x 3 = 108
d. Aantal mogelijke combinaties: 6 x 10 x 10 = 600
41.
a. Aantal mogelijke combinaties: 24 x 24 = 576
b. Aantal mogelijke combinaties: 24 x 23 = 552
c. Kies methode 2. Bij methode 1 loop je de kans dat 1 persoon 2x wint. Dat is minder eerlijk.
42.
Tip:
Voorbeeld van MET herhaling: ABCA en voorbeeld van ZONDER herhaling: ABCG
a. 7 x 6 x 5 x 4 = 840 Voorbeeld van MET herhaling: ABCA en voorbeeld van ZONDER herhaling: ABCG
b. 7 x 7 x 7 x 7 = 2401
c. 1 x 1 x 7 x 7 = 49
d. 1 x 1 x 5 x 4 = 20
43.
a. 10 x 10 x 10 x 10 = 10 000
b. 10 x 9 x 8 x 7 = 5040
c. 10 x 1 x 1 x 1 = 10
d. 5 x 5 x 5 x 5 = 625
44.
Tip:
3-lettercode wil zeggen dat je 3 hokjes hebt waar je iets in kunt zetten. Bij een 4-lettercode heb je dus 4 hokjes waar je iets in kunt zetten.
a.
Zonder herhaling: 7 x 6 x 5 = 2103-lettercode wil zeggen dat je 3 hokjes hebt waar je iets in kunt zetten. Bij een 4-lettercode heb je dus 4 hokjes waar je iets in kunt zetten.
Met herhaling: 7 x 7 x 7 x 7 = 2401
b. 5-lettercode MET herhaling: 7 x 7 x 7 x 7 x 7 = 16 807
5-lettercode ZONDER herhaling: 7 x 6 x 5 x 4 x 3 = 2520
Het verschil is inderdaad groter dan 14 000.
45.
a. Aantal mogelijke combinaties: 4 x 4 x 4 x 4 = 256
b. Aantal mogelijke combinaties: 1 x 4 x 4 x 4 = 64
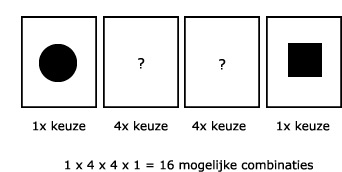
c. Aantal mogelijke combinaties: 1 x 4 x 4 x 1 = 16 (zie afbeelding)
d. Aantal mogelijke combinaties: 4 x 3 x 2 x 1 = 24
46.
a. 218 = 262 144
b. 114 x 24 = 16
c. 16 x 212 = 4096
47.
a. Aantal mogelijke combinaties: 16 x 13 x 27 = 5616
b. Aantal mogelijke combinaties: 13 x 16 x 15 = 3120
c. Aantal mogelijke combinaties: 13 x 12 x 11 = 1716
48.
a. Aantal mogelijke combinaties: 6 x 5 x 4 x 3 = 360
b. Aantal mogelijke combinaties: 2 x 5 x 4 x 3 = 120
c. Aantal mogelijke combinaties: 6 x 6 x 6 x 3 = 648
49.
a. Aantal mogelijke combinaties: 8 x 7 x 6 = 366
b. Aantal mogelijke combinaties: 6 x 5 x 4 x 3 = 360
c. Aantal mogelijke combinaties: 412 = 16 777 216
d. Aantal mogelijke combinaties: 10 x 9 x 8 x 7 x 6 x 5 = 151 200
e.
- 5 x 5 x 5 x 5 = 54 = 625
- 21 x 21 x 21 x 21 = 214 = 194 481
- 26 x 25 x 24 x 23 = 358 800
- 5 x 21 x 5 x 21 = 11 025
50.
a. aantal = 2 x 4 = 8
b. aantal = 3 x 2 = 6
c. totaal = 14
51.
a. r-r-r of gr-gr-gr of g-g-g levert 3 + 1 + 4 = 8 manieren
b. r-gr-gr of r-g-g levert 3 + 6 = 9 manieren
52.
APQB = 2 x 3 x 3 = 18
AQB = 1 x 3 = 3
53.
a. 12 x 5 x 6 = 360
b. 12 x 11 = 132
54.
b. 46 x 45 = 2070
c. mm of jj levert (52 x 51) + (46 x 45) = 4722
d. (28 x 27) + (50 x 49) + (20 x 19) = 3586
a. Aantal mogelijke combinaties: 4 x 4 x 4 x 4 = 256
b. Aantal mogelijke combinaties: 1 x 4 x 4 x 4 = 64
c. Aantal mogelijke combinaties: 1 x 4 x 4 x 1 = 16 (zie afbeelding)
d. Aantal mogelijke combinaties: 4 x 3 x 2 x 1 = 24

46.
a. 218 = 262 144
b. 114 x 24 = 16
c. 16 x 212 = 4096
47.
a. Aantal mogelijke combinaties: 16 x 13 x 27 = 5616
b. Aantal mogelijke combinaties: 13 x 16 x 15 = 3120
c. Aantal mogelijke combinaties: 13 x 12 x 11 = 1716
48.
a. Aantal mogelijke combinaties: 6 x 5 x 4 x 3 = 360
b. Aantal mogelijke combinaties: 2 x 5 x 4 x 3 = 120
c. Aantal mogelijke combinaties: 6 x 6 x 6 x 3 = 648
49.
a. Aantal mogelijke combinaties: 8 x 7 x 6 = 366
b. Aantal mogelijke combinaties: 6 x 5 x 4 x 3 = 360
c. Aantal mogelijke combinaties: 412 = 16 777 216
d. Aantal mogelijke combinaties: 10 x 9 x 8 x 7 x 6 x 5 = 151 200
e.
- 5 x 5 x 5 x 5 = 54 = 625
- 21 x 21 x 21 x 21 = 214 = 194 481
- 26 x 25 x 24 x 23 = 358 800
- 5 x 21 x 5 x 21 = 11 025
50.
a. aantal = 2 x 4 = 8
b. aantal = 3 x 2 = 6
c. totaal = 14
51.
a. r-r-r of gr-gr-gr of g-g-g levert 3 + 1 + 4 = 8 manieren
b. r-gr-gr of r-g-g levert 3 + 6 = 9 manieren
52.
Tip:
Je kan lopen via APQB en via AQB.
Dat kan op 18 + 3 = 21 manieren.Je kan lopen via APQB en via AQB.
APQB = 2 x 3 x 3 = 18
AQB = 1 x 3 = 3
53.
a. 12 x 5 x 6 = 360
b. 12 x 11 = 132
54.
Tip:
Bij d. even oud? Doe dan: 14-14 of 15-15 of 16-16
a. 14 x 19 = 266Bij d. even oud? Doe dan: 14-14 of 15-15 of 16-16
b. 46 x 45 = 2070
c. mm of jj levert (52 x 51) + (46 x 45) = 4722
d. (28 x 27) + (50 x 49) + (20 x 19) = 3586
55.
a. 120 en 40 320
b. 5! = 120 en 8! = 40 320
c. 5! = 5 x 4 x 3 x 2 x 1
d. n!
e. *
f. *
a. 120 en 40 320
b. 5! = 120 en 8! = 40 320
c. 5! = 5 x 4 x 3 x 2 x 1
d. n!
e. *
f. *
Andere paragrafen:
9.1. Centrummaten en verdelingen (1 t/m 13)
9.2. Spreiding en boxplot (14 t/m 26)
9.3. Spreidingsdiagrammen (27 t/m 34)
9.4. Tellen met en zonder herhaling (35 t/m 55)
9.1. Centrummaten en verdelingen (1 t/m 13)
9.2. Spreiding en boxplot (14 t/m 26)
9.3. Spreidingsdiagrammen (27 t/m 34)
9.4. Tellen met en zonder herhaling (35 t/m 55)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


