TIP: Wil je ook toegang tot meer dan 16.900 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 5.1 Lineaire formules VWO 2
Boek: Getal & Ruimte - Vergelijkingen VWO 2 (deel 1) opgaven 1 t/m 12, 2009De basisformule voor een lijn is: y = ax + b, waarbij je voor a en b waarden kunt invullen.
Bedenk hierbij dat:
- a: 1 naar rechts is a omhoog
- b: de lijn de y-as snijdt in het punt (0,b)
Om een lijn te tekenen, heb je maar 2 punten nodig. Maak altijd een tabel. We noemen dit ook wel een visgraat.
Voorbeelden van lineaire formules zijn: y = -3x + 6 of N = 1/2t - 4
Teken een lijn altijd netjes met je geodriehoek.
Bedenk hierbij dat:
- a: 1 naar rechts is a omhoog
- b: de lijn de y-as snijdt in het punt (0,b)
Om een lijn te tekenen, heb je maar 2 punten nodig. Maak altijd een tabel. We noemen dit ook wel een visgraat.
Voorbeelden van lineaire formules zijn: y = -3x + 6 of N = 1/2t - 4
Teken een lijn altijd netjes met je geodriehoek.
1.
b.
c. Uit de tabel volgt de punten: (-2,1), (0,2), (2,3), (4,4), (6,5)
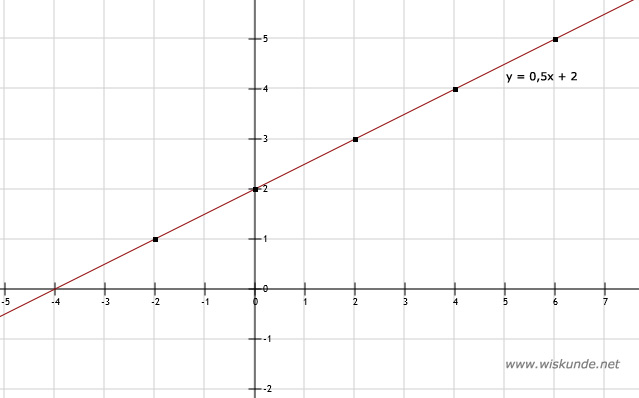
2.
b.
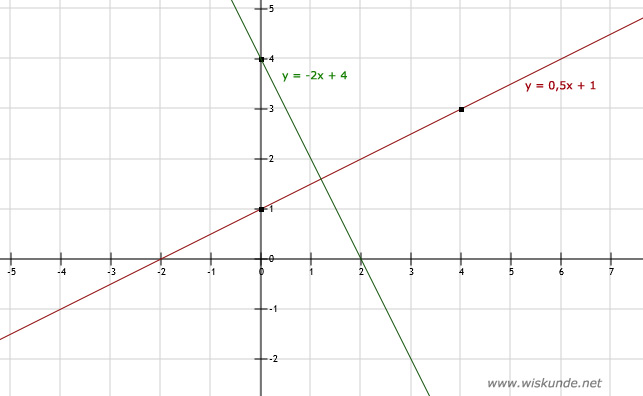
3.
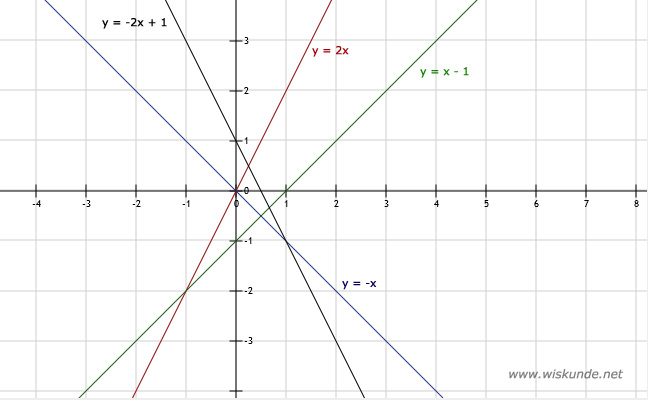
4.
b. Het snijpunt van deze 2 lijnen is: (2,-1)
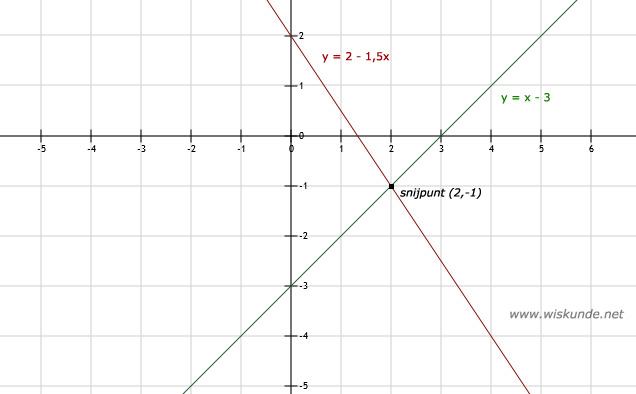
5.
b. Bij t = 2 krijg je als B-waarde 3,2. Dat tekent lastig in een assenstelsel want het is geen exact roosterpunt.
Nog een goede waarde is bij t = 10 of t = -5.
c. Zie afbeelding

6.
b. (groen)
7.
b. Zie afbeelding
8.
b. B = 200 + 15 ⋅ 4,5 = 200 + 67,50 = 267,50 euro
c. B = 200 + 15 ⋅ 0 = 200 + 0 = 200 euro
d. 200 is een vast basisbedrag en 15 is de variabele prijs per 1000 views.
9.
b. De grafiek snijdt de y-as in (0,3).
c. 3
d. Snijdt de y-as in (0,-8).
10.
Snijden in de y-as: y = 2x + 2 en y = 0,5x + 2.
Dat zie je omdat ze gelijke b-waarde hebben (y = ax + b). De waarde van b is dus 2.
b.
Evenwijdig zijn: y = 0,5x - 4 en y = 0,5x + 2.
Dat zie je omdat ze gelijke a-waarde hebben (y = ax + b). De waarde van a is dus 0,5.
Tip:
Alle punten liggen op een rechte lijn. Deze punten krijg je door in de formule een waarde voor x in te vullen. Je krijgt dan ook de y-waarde van het coördinaat (x,y).
a. y = 0,5 ⋅ -2 + 2 = -1 + 2 = 1Alle punten liggen op een rechte lijn. Deze punten krijg je door in de formule een waarde voor x in te vullen. Je krijgt dan ook de y-waarde van het coördinaat (x,y).
b.
| x | -2 | 0 | 2 | 4 | 6 |
| y | 1 | 2 | 3 | 4 | 5 |
c. Uit de tabel volgt de punten: (-2,1), (0,2), (2,3), (4,4), (6,5)

2.
Tip:
Kies in de tabel altijd x = 0. Dit rekent altijd makkelijk.
a. Kies in de tabel altijd x = 0. Dit rekent altijd makkelijk.
| x | 0 | 4 |
| y | 1 | 3 |
b.
| x | 0 | 4 |
| y | 4 | -4 |

3.
Tip:
Kies 2 punten per lijn en teken dan de lijn.
Zie afbeelding
Kies 2 punten per lijn en teken dan de lijn.

4.
Tip:
Bij x = 0 heb je het snijpunt met de y-as.
a. Zie afbeeldingBij x = 0 heb je het snijpunt met de y-as.
b. Het snijpunt van deze 2 lijnen is: (2,-1)

5.
Tip:
Het is handig om 2 punten te kiezen voor een lijn die beide wel roosterpunten zijn.
In deze opgave hebben we een t-as en een B-as i.p.v. een x-as en y-as. Maar het komt op hetzelfde neer.
a. Het is handig om 2 punten te kiezen voor een lijn die beide wel roosterpunten zijn.
In deze opgave hebben we een t-as en een B-as i.p.v. een x-as en y-as. Maar het komt op hetzelfde neer.
| t | 0 | 5 |
| B | 2 | 5 |
b. Bij t = 2 krijg je als B-waarde 3,2. Dat tekent lastig in een assenstelsel want het is geen exact roosterpunt.
Nog een goede waarde is bij t = 10 of t = -5.
c. Zie afbeelding

6.
Tip:
Ik heb ze nu even in 1 plaatje gedaan.
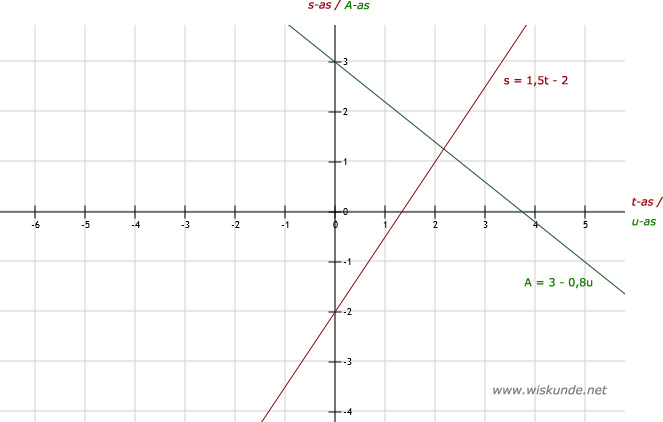
a. (rood)Ik heb ze nu even in 1 plaatje gedaan.
| t | 0 | 4 |
| s | -2 | 4 |
b. (groen)
| u | 0 | 5 |
| A | 3 | -1 |

7.
Tip:
Een assenstelsel hoeft niet altijd in stappen van 1 te zijn. Kan ook 10 of 20 zijn.
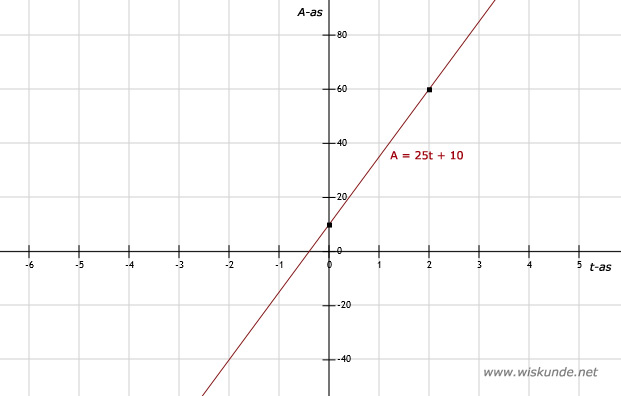
a. Een assenstelsel hoeft niet altijd in stappen van 1 te zijn. Kan ook 10 of 20 zijn.
| t | 0 | 2 |
| A | 10 | 60 |
b. Zie afbeelding

8.
Tip:
v is in duizendtallen. Dus bij 6000 bezoekers is v gelijk aan 6.
a. Te betalen: B = 200 + 15 ⋅ 6 = 200 + 90 = 290 eurov is in duizendtallen. Dus bij 6000 bezoekers is v gelijk aan 6.
b. B = 200 + 15 ⋅ 4,5 = 200 + 67,50 = 267,50 euro
c. B = 200 + 15 ⋅ 0 = 200 + 0 = 200 euro
d. 200 is een vast basisbedrag en 15 is de variabele prijs per 1000 views.
9.
Tip:
Bij y = ax + b is het snijpunt met de y-as: (0,b).
Vul voor x maar 0 in dan zie je dat de y-waarde gelijk is aan b.
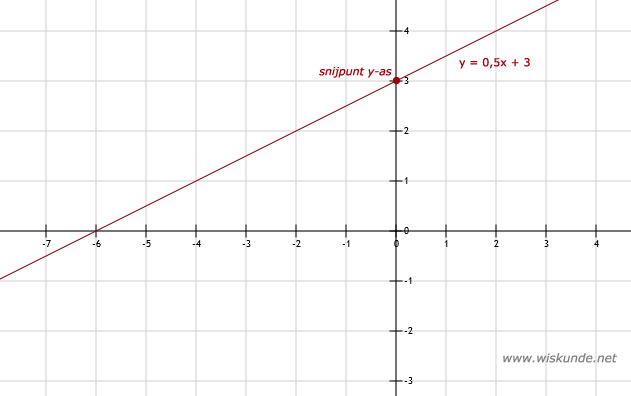
a. Bij y = ax + b is het snijpunt met de y-as: (0,b).
Vul voor x maar 0 in dan zie je dat de y-waarde gelijk is aan b.
| x | 0 | 2 |
| y | 3 | 4 |
b. De grafiek snijdt de y-as in (0,3).
c. 3
d. Snijdt de y-as in (0,-8).

10.
Tip:
Grafieken die dezelfde a-waarde hebben (y = ax + b) zijn evenwijdig. Ze hebben dan gelijke richtingscoefficiënt.
Grafieken die dezelfde b-waarde hebben (y = ax + b) snijden elkaar in de y-as in punt (0,b).
a.Grafieken die dezelfde a-waarde hebben (y = ax + b) zijn evenwijdig. Ze hebben dan gelijke richtingscoefficiënt.
Grafieken die dezelfde b-waarde hebben (y = ax + b) snijden elkaar in de y-as in punt (0,b).
Snijden in de y-as: y = 2x + 2 en y = 0,5x + 2.
Dat zie je omdat ze gelijke b-waarde hebben (y = ax + b). De waarde van b is dus 2.
b.
Evenwijdig zijn: y = 0,5x - 4 en y = 0,5x + 2.
Dat zie je omdat ze gelijke a-waarde hebben (y = ax + b). De waarde van a is dus 0,5.
11.
y = 5x + 7 en y = 5x + 3 (i.v.m. 5)
y = -0,2x + 1 en y = -0,2x + 3 (i.v.m. -0,2)
b. Hetzelfde snijpunt met de y-as:
y = 5x + 7 en y = -4x + 7 (i.v.m. 7)
y = 4x + 3 en y = 5x + 3 en y = -0,2x + 3 (i.v.m. 3)
12.
b. t = 50 invullen levert: h = -5 ⋅ 50 + 750 = 500 (meter)
t = 60 invullen levert: h = -5 ⋅ 60 + 750 = 450 (meter)
c. Zie afbeelding
d. Bij t = 150 geldt: h = -5 ⋅ 150 + 750 = -750 + 750 = 0 (meter)
Dus bij t = 150 (seconden) is de hoogte gelijk aan 0 (meter). Je krijgt dan het punt (150,0). Dit is het snijpunt met de x-as.
e. Per seconde daalt de parachute 5 meter.
Tip:
Het getal voor de x noemen we ook wel de richtingscoefficiënt.
a. Evenwijdig zijn:Het getal voor de x noemen we ook wel de richtingscoefficiënt.
y = 5x + 7 en y = 5x + 3 (i.v.m. 5)
y = -0,2x + 1 en y = -0,2x + 3 (i.v.m. -0,2)
b. Hetzelfde snijpunt met de y-as:
y = 5x + 7 en y = -4x + 7 (i.v.m. 7)
y = 4x + 3 en y = 5x + 3 en y = -0,2x + 3 (i.v.m. 3)
12.
Tip:
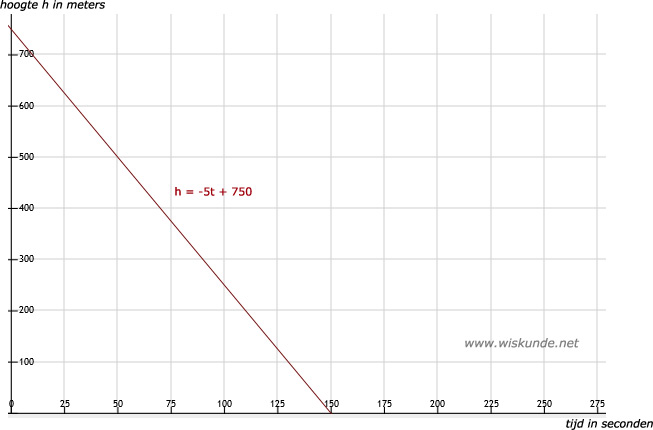
De grafiek heeft geen negatieve assen. Want negatieve seconden en negatieve hoogte bestaan niet.
a. t = 0 invullen levert: h = -5 ⋅ 0 + 750 = 750 (meter)De grafiek heeft geen negatieve assen. Want negatieve seconden en negatieve hoogte bestaan niet.
b. t = 50 invullen levert: h = -5 ⋅ 50 + 750 = 500 (meter)
t = 60 invullen levert: h = -5 ⋅ 60 + 750 = 450 (meter)
c. Zie afbeelding
d. Bij t = 150 geldt: h = -5 ⋅ 150 + 750 = -750 + 750 = 0 (meter)
Dus bij t = 150 (seconden) is de hoogte gelijk aan 0 (meter). Je krijgt dan het punt (150,0). Dit is het snijpunt met de x-as.
e. Per seconde daalt de parachute 5 meter.

Andere paragrafen:
5.1. Lineaire formules (1 t/m 12)
5.2. De richtingscoëfficiënt van een lijn (13 t/m 19)
5.3. De formule van een lijn opstellen (20 t/m 30)
5.4. De balansmethode (31 t/m 46)
5.5. Vergelijkingen oplossen (47 t/m 59)
5.6. Vergelijkingen toepassen (60 t/m 73)
5.1. Lineaire formules (1 t/m 12)
5.2. De richtingscoëfficiënt van een lijn (13 t/m 19)
5.3. De formule van een lijn opstellen (20 t/m 30)
5.4. De balansmethode (31 t/m 46)
5.5. Vergelijkingen oplossen (47 t/m 59)
5.6. Vergelijkingen toepassen (60 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


