TIP: Wil je ook toegang tot meer dan 17.100 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 5.6 Vergelijkingen toepassen VWO 2
Boek: Getal & Ruimte - Vergelijkingen VWO 2 (deel 1) opgaven 60 t/m 73, 2009
60.
a.
Kosten per maand = 17 + 0,74 x 43 = 48,82 euro
b.
53 + 0,29x = 71,27
Nu links en rechts -53
0,29x = 18,27
Nu links en rechts :0,29
x = 18,27/0,29 = 63
Dus ze heeft 63 minuten gebeld in oktober.
c.
17 + 0,74x = 53 + 0,29x
Nu links en rechts -0,29x
17 + 0,45x = 53
Nu links en rechts -17
0,45x = 36
Nu links en rechts :0,45
x = 36/0,45 = 80
Bij 80 minuten bellen, zijn beide bedrijven even duur.
61.
Hij stijgt 600 meter. Dus het aantal keer dat hij 100 meter stijgt, is dus 6. Hieruit volgt h = 6
4½ uur = 4½ x 60 minuten = 270 minuten.
b.
A = 15k + 15h + 30
270 = 15k + 15⋅6 + 30
270 = 15k + 90 + 30
270 = 15k + 120
15k + 120 = 270
Nu links en rechts -120
15k = 150
Nu links en rechts :15
k = 150/15 = 10
Dus hij heeft 10 km gewandeld.
c.
6 uur en 1 kwartier = 360 + 15 = 375 minuten
A = 15k + 15h + 30 (vul in wat je weet:)
375 = 15⋅18 + 15h + 30
375 = 270 + 15h + 30
375 = 300 + 15h
300 + 15h = 375
Nu links en rechts -300
15h = 75
Nu links en rechts :15
h = 75/15 = 5
d.
Dus tijdens de wandeling is hij 5x 100 meter gestegen. Dus hij is 500 meter gestegen.
62.
Kinderen zijn kleiner en zullen daardoor minder medicijnen nodig hebben dan een volwassene.
b.
y = 1/24(t + 1)⋅a
t = 5 (jaar)
a = 4 (mg)
Vul in wat je weet:
y = 1/24(5 + 1)⋅4
y = 1/24 ⋅ 6 ⋅ 4
y = 1
Dus Jan mag 1 mg op een dag nemen.
c.
y = 3 (mg)
t = 11 (jaar)
Vul in wat je weet:
y = 1/24(t + 1)⋅a
3 = 1/24(11 + 1)⋅a
3 = 1/24 ⋅ 12 ⋅ a
3 = 12/24 ⋅ a
3 = 1/2a
1/2a = 3
Nu links en rechts x2
a = 6
Dus een volwassene mag dan 6 mg nemen.
d.
Carla is een kind, dus y = 4 mg.
Bij haar moeder hoort a = 12 mg.
Vul in wat je weet:
y = 1/24(t + 1)⋅a
4 = 1/24(t + 1)⋅12
4 = 12/24(t + 1)
4 = 1/2(t + 1)
1/2(t + 1) = 4
Nu links en rechts x2
t + 1 = 8
Nu links en rechts -1
t = 7
Dus Carla is 7 jaar en haar moeder is 4 x 7 = 28 jaar oud.
63.
3x - 45 = 1/2x
b.
3x - 45 = ½x
Nu links en rechts -½x
2½x - 45 = 0
Nu links en rechts +45
2½x = 45
Nu links en rechts *2 (keer 2)
5x = 90
Nu links en rechts :5
x = 90/5 = 18
64.
2(x + 3) = 3x - 7
b.
2(x + 3) = 3x - 7
2x + 6 = 3x - 7
Nu links en rechts -3x
-x + 6 = -7
Nu links en rechts -6
-x = -13
Nu links en rechts :-1
x = -13/-1 = 13
Hij had dus het getal 13 in gedachten.
65.
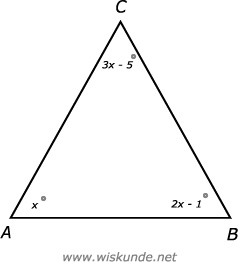
x + (2x - 1) + (3x - 5) = 180
6x - 6 = 180
Nu links en rechts +6
6x = 186
Nu links en rechts :6
x = 186/6 = 31
Dus de hoeken zijn:
∠A = x = 31º
∠B = 2x - 1 = 2⋅31 - 1 = 62 - 1 = 61º
∠C = 3x - 5 = 3⋅31 - 5 = 93 - 5 = 88º
Controleer: 31º + 61º + 88º = 180º, dus het klopt!
66.
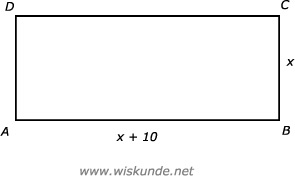
Omtrek = AB + BC + CD + AD
94 = (x + 10) + x + (x + 10) + x
94 = 4x + 20
b.
Los op: 94 = 4x + 20
4x + 20 = 94
Nu links en rechts -20
4x = 74
Nu links en rechts :4
x = 74/4 = 18,5
Dus:
AB = (x + 10) = 18,5 + 10 = 28,5
BC = x = 18,5
CD = (x + 10) = 18,5 + 10 = 28,5
AD = x = 18,5
67.
x + 12 = 3x - 144
Nu links en rechts -3x
-2x + 12 = -144
Nu links en rechts -12
-2x = -156
Nu links en rechts :-2
x = -156/-2 = 78
Dus tante Annie is vandaag de dag 78 jaar oud.
68.
aantal gelijk gespeeld: 24 - 2x
b.
aantal punten na 24 wedstrijden:
- punten bij winst: 3x
- punten bij gelijk: (24 - 2x)
- punten bij verlies: 0
Dus het totaal aantal punten na 24 wedstrijden:
winst + gelijk + verlies = 31
3x + (24 - 2x) + 0 = 31
3x + 24 - 2x = 31
x + 24 = 31
Nu links en rechts -24
x = 7
Dus de club heeft 7 wedstrijden gewonnen.
Controleer: 7 wedstrijden gewonnen en dus ook 7 verloren. Dat betekent dus 10 wedstrijden gelijkgespeeld.
Aantal punten dus: 7*3 + 10*1 + 7*0 = 21 + 10 + 0 = 31 punten. Ja, het klopt!
69.
x + x + (x + 6) = 78
3x + 6 = 78
b.
Los op: 3x + 6 = 78
Nu links en rechts -6
3x = 72
Nu links en rechts :3
x = 72/3 = 24
Dus de tweeling is 24 jaar oud.
Controleer: 24 + 24 + 30 = 78 jaar. Ja, het klopt!
a.
Kosten per maand = 17 + 0,74 x 43 = 48,82 euro
b.
53 + 0,29x = 71,27
Nu links en rechts -53
0,29x = 18,27
Nu links en rechts :0,29
x = 18,27/0,29 = 63
Dus ze heeft 63 minuten gebeld in oktober.
c.
17 + 0,74x = 53 + 0,29x
Nu links en rechts -0,29x
17 + 0,45x = 53
Nu links en rechts -17
0,45x = 36
Nu links en rechts :0,45
x = 36/0,45 = 80
Bij 80 minuten bellen, zijn beide bedrijven even duur.
61.
Tip:
Schrijf de formule over in je schrift.
Het overschrijven van een formule leidt tot een beter inzicht van de formule.
A = 15k + 15h + 30
En vul daarna in wat je weet.
a. Schrijf de formule over in je schrift.
Het overschrijven van een formule leidt tot een beter inzicht van de formule.
A = 15k + 15h + 30
En vul daarna in wat je weet.
Hij stijgt 600 meter. Dus het aantal keer dat hij 100 meter stijgt, is dus 6. Hieruit volgt h = 6
4½ uur = 4½ x 60 minuten = 270 minuten.
b.
A = 15k + 15h + 30
270 = 15k + 15⋅6 + 30
270 = 15k + 90 + 30
270 = 15k + 120
15k + 120 = 270
Nu links en rechts -120
15k = 150
Nu links en rechts :15
k = 150/15 = 10
Dus hij heeft 10 km gewandeld.
c.
6 uur en 1 kwartier = 360 + 15 = 375 minuten
A = 15k + 15h + 30 (vul in wat je weet:)
375 = 15⋅18 + 15h + 30
375 = 270 + 15h + 30
375 = 300 + 15h
300 + 15h = 375
Nu links en rechts -300
15h = 75
Nu links en rechts :15
h = 75/15 = 5
d.
Dus tijdens de wandeling is hij 5x 100 meter gestegen. Dus hij is 500 meter gestegen.
62.
Tip:
Schrijf de formule over en vul steeds in wat je weet.
a. Schrijf de formule over en vul steeds in wat je weet.
Kinderen zijn kleiner en zullen daardoor minder medicijnen nodig hebben dan een volwassene.
b.
y = 1/24(t + 1)⋅a
t = 5 (jaar)
a = 4 (mg)
Vul in wat je weet:
y = 1/24(5 + 1)⋅4
y = 1/24 ⋅ 6 ⋅ 4
y = 1
Dus Jan mag 1 mg op een dag nemen.
c.
y = 3 (mg)
t = 11 (jaar)
Vul in wat je weet:
y = 1/24(t + 1)⋅a
3 = 1/24(11 + 1)⋅a
3 = 1/24 ⋅ 12 ⋅ a
3 = 12/24 ⋅ a
3 = 1/2a
1/2a = 3
Nu links en rechts x2
a = 6
Dus een volwassene mag dan 6 mg nemen.
d.
Carla is een kind, dus y = 4 mg.
Bij haar moeder hoort a = 12 mg.
Vul in wat je weet:
y = 1/24(t + 1)⋅a
4 = 1/24(t + 1)⋅12
4 = 12/24(t + 1)
4 = 1/2(t + 1)
1/2(t + 1) = 4
Nu links en rechts x2
t + 1 = 8
Nu links en rechts -1
t = 7
Dus Carla is 7 jaar en haar moeder is 4 x 7 = 28 jaar oud.
63.
Tip:
Stel het getal gelijk aan x. Als je dat getal met 3 vermenigvuldigt, krijg je 3x. Als je daar 45 van aftrekt, krijg je 3x - 45.
Als de uitkomst dan gelijk is aan de helft van x (oorspronkelijk getal), krijg je als vergelijking om op te lossen: 3x - 45 = 1/2x.
a. Stel het getal gelijk aan x. Als je dat getal met 3 vermenigvuldigt, krijg je 3x. Als je daar 45 van aftrekt, krijg je 3x - 45.
Als de uitkomst dan gelijk is aan de helft van x (oorspronkelijk getal), krijg je als vergelijking om op te lossen: 3x - 45 = 1/2x.
3x - 45 = 1/2x
b.
3x - 45 = ½x
Nu links en rechts -½x
2½x - 45 = 0
Nu links en rechts +45
2½x = 45
Nu links en rechts *2 (keer 2)
5x = 90
Nu links en rechts :5
x = 90/5 = 18
64.
Tip:
Stel het getal gelijk aan x.
Als je dat getal met 3 vermeerdert (optelt), krijg je x + 3.
Als je dan de uitkomst verdubbelt (keer 2), krijg je 2(x + 3).
Dit moet gelijk zijn aan het volgende:
Als je x met 3 vermenigvuldigt, krijg je 3x. Als je daar 7 van aftrekt, krijg je 3x - 7.
a. Stel het getal gelijk aan x.
Als je dat getal met 3 vermeerdert (optelt), krijg je x + 3.
Als je dan de uitkomst verdubbelt (keer 2), krijg je 2(x + 3).
Dit moet gelijk zijn aan het volgende:
Als je x met 3 vermenigvuldigt, krijg je 3x. Als je daar 7 van aftrekt, krijg je 3x - 7.
2(x + 3) = 3x - 7
b.
2(x + 3) = 3x - 7
2x + 6 = 3x - 7
Nu links en rechts -3x
-x + 6 = -7
Nu links en rechts -6
-x = -13
Nu links en rechts :-1
x = -13/-1 = 13
Hij had dus het getal 13 in gedachten.
65.
Tip:
Hoekensom van een driehoek is 180 graden.
Stel hoek A is gelijk aan x graden en hoek B is gelijk aan (2x - 1) graden.
Hoekensom = 180:Hoekensom van een driehoek is 180 graden.
Stel hoek A is gelijk aan x graden en hoek B is gelijk aan (2x - 1) graden.
x + (2x - 1) + (3x - 5) = 180
6x - 6 = 180
Nu links en rechts +6
6x = 186
Nu links en rechts :6
x = 186/6 = 31
Dus de hoeken zijn:
∠A = x = 31º
∠B = 2x - 1 = 2⋅31 - 1 = 62 - 1 = 61º
∠C = 3x - 5 = 3⋅31 - 5 = 93 - 5 = 88º
Controleer: 31º + 61º + 88º = 180º, dus het klopt!

66.
Tip:
Maak eerst een schets. Stel BC = x. Dan is AB dus gelijk aan x + 10.
Omtrek = AB + BC + CD + AD
a.Maak eerst een schets. Stel BC = x. Dan is AB dus gelijk aan x + 10.
Omtrek = AB + BC + CD + AD
Omtrek = AB + BC + CD + AD
94 = (x + 10) + x + (x + 10) + x
94 = 4x + 20
b.
Los op: 94 = 4x + 20
4x + 20 = 94
Nu links en rechts -20
4x = 74
Nu links en rechts :4
x = 74/4 = 18,5
Dus:
AB = (x + 10) = 18,5 + 10 = 28,5
BC = x = 18,5
CD = (x + 10) = 18,5 + 10 = 28,5
AD = x = 18,5

67.
Tip:
Stel dat ze vandaag x jaar oud is.
Dan is ze over 12 jaar: (x + 12)
48 jaar geleden is: (x - 48)
3 jaar zo oud als 48 jaar geleden: 3(x - 48)
(x + 12) = 3(x - 48)Stel dat ze vandaag x jaar oud is.
Dan is ze over 12 jaar: (x + 12)
48 jaar geleden is: (x - 48)
3 jaar zo oud als 48 jaar geleden: 3(x - 48)
x + 12 = 3x - 144
Nu links en rechts -3x
-2x + 12 = -144
Nu links en rechts -12
-2x = -156
Nu links en rechts :-2
x = -156/-2 = 78
Dus tante Annie is vandaag de dag 78 jaar oud.
68.
Tip:
Stel: aantal 'gewonnen' wedstrijden gelijk aan x.
Dan is dus het aantal 'verloren' wedstrijden ook gelijk aan x (dat is gezegd).
Dus aantal 'gelijk' gespeelde wedstrijden: 24 - x - x = 24 - 2x
a.Stel: aantal 'gewonnen' wedstrijden gelijk aan x.
Dan is dus het aantal 'verloren' wedstrijden ook gelijk aan x (dat is gezegd).
Dus aantal 'gelijk' gespeelde wedstrijden: 24 - x - x = 24 - 2x
aantal gelijk gespeeld: 24 - 2x
b.
aantal punten na 24 wedstrijden:
- punten bij winst: 3x
- punten bij gelijk: (24 - 2x)
- punten bij verlies: 0
Dus het totaal aantal punten na 24 wedstrijden:
winst + gelijk + verlies = 31
3x + (24 - 2x) + 0 = 31
3x + 24 - 2x = 31
x + 24 = 31
Nu links en rechts -24
x = 7
Dus de club heeft 7 wedstrijden gewonnen.
Controleer: 7 wedstrijden gewonnen en dus ook 7 verloren. Dat betekent dus 10 wedstrijden gelijkgespeeld.
Aantal punten dus: 7*3 + 10*1 + 7*0 = 21 + 10 + 0 = 31 punten. Ja, het klopt!
69.
Tip:
broer1 en broer2 (tweeling) zijn even oud: x jaar
broer1 + broer2 + broer3 = 78
x + x + (x + 6) = 78
a.broer1 en broer2 (tweeling) zijn even oud: x jaar
broer1 + broer2 + broer3 = 78
x + x + (x + 6) = 78
x + x + (x + 6) = 78
3x + 6 = 78
b.
Los op: 3x + 6 = 78
Nu links en rechts -6
3x = 72
Nu links en rechts :3
x = 72/3 = 24
Dus de tweeling is 24 jaar oud.
Controleer: 24 + 24 + 30 = 78 jaar. Ja, het klopt!
70.
x + (x + 2) + (x + 4) = 171
b.
x + (x + 2) + (x + 4) = 171
3x + 6 = 171
Nu links en rechts -6
3x = 165
Nu links en rechts :3
x = 165/3 = 55
Dus:
1e oneven getal = x = 55
2e oneven getal = (x + 2) = 55 + 2 = 57
3e oneven getal = (x + 4) = 55 + 4 = 59
Controleer: 55 + 57 + 59 = 171, dus het klopt!
71.
3x + 9 = 45
Nu links en rechts -9
3x = 36
Nu links en rechts :3
x = 36/3 = 12
Dus:
Leeftijd Dick = x = 12
Leeftijd Tom (2 jaar ouder dan Dick) = (x + 2) = 12 + 2 = 14
Leeftijd Mark (7 jaar ouder dan Dick) = (x + 7) = 12 + 7 = 19
Controleer: 12 + 14 + 19 = 45, dus het klopt!
72.
Nu links en rechts *84 (keer 84)
84⋅(1/6)x + 84⋅(1/12)x + 84⋅(1/7)x + 84⋅5 + 84⋅(1/2)x + 84⋅4 = 84⋅x
14x + 7x + 12x + 420 + 42x + 336 = 84x
75x + 756 = 84x
Nu links en rechts -84x
-9x + 756 = 0
Nu links en rechts -756
-9x = -756
Nu links en rechts :-9
x = -756/-9 = 84
Dus Diophantus werd 84 jaar oud.
Tip:
Stel het 1e oneven getal gelijk aan x, dan is het volgende oneven getal 2 verder.
Bijvoorbeeld 21 en dan 2 verder is 23. Dus neem (x + 2) als 2e oneven getal.
Het 3e oneven getal is dan weer 2 verder, dus dat wordt (x + 4).
a.Stel het 1e oneven getal gelijk aan x, dan is het volgende oneven getal 2 verder.
Bijvoorbeeld 21 en dan 2 verder is 23. Dus neem (x + 2) als 2e oneven getal.
Het 3e oneven getal is dan weer 2 verder, dus dat wordt (x + 4).
x + (x + 2) + (x + 4) = 171
b.
x + (x + 2) + (x + 4) = 171
3x + 6 = 171
Nu links en rechts -6
3x = 165
Nu links en rechts :3
x = 165/3 = 55
Dus:
1e oneven getal = x = 55
2e oneven getal = (x + 2) = 55 + 2 = 57
3e oneven getal = (x + 4) = 55 + 4 = 59
Controleer: 55 + 57 + 59 = 171, dus het klopt!
71.
Tip:
Stel: leeftijd van Dick gelijk aan x.
Tom + Dick + Mark = 45
(x + 2) + x + (x + 7) = 45
Vergelijking: (x + 2) + x + (x + 7) = 45Stel: leeftijd van Dick gelijk aan x.
Tom + Dick + Mark = 45
(x + 2) + x + (x + 7) = 45
3x + 9 = 45
Nu links en rechts -9
3x = 36
Nu links en rechts :3
x = 36/3 = 12
Dus:
Leeftijd Dick = x = 12
Leeftijd Tom (2 jaar ouder dan Dick) = (x + 2) = 12 + 2 = 14
Leeftijd Mark (7 jaar ouder dan Dick) = (x + 7) = 12 + 7 = 19
Controleer: 12 + 14 + 19 = 45, dus het klopt!
72.
Tip:
Stel het aantal jaren dat Diophantus heeft geleefd gelijk aan x jaar.
(1/6)x + (1/12)x + (1/7)x + 5 + (1/2)x + 4 = x
(1/6)x + (1/12)x + (1/7)x + 5 + (1/2)x + 4 = xStel het aantal jaren dat Diophantus heeft geleefd gelijk aan x jaar.
(1/6)x + (1/12)x + (1/7)x + 5 + (1/2)x + 4 = x
Nu links en rechts *84 (keer 84)
84⋅(1/6)x + 84⋅(1/12)x + 84⋅(1/7)x + 84⋅5 + 84⋅(1/2)x + 84⋅4 = 84⋅x
14x + 7x + 12x + 420 + 42x + 336 = 84x
75x + 756 = 84x
Nu links en rechts -84x
-9x + 756 = 0
Nu links en rechts -756
-9x = -756
Nu links en rechts :-9
x = -756/-9 = 84
Dus Diophantus werd 84 jaar oud.
Andere paragrafen:
5.1. Lineaire formules (1 t/m 12)
5.2. De richtingscoëfficiënt van een lijn (13 t/m 19)
5.3. De formule van een lijn opstellen (20 t/m 30)
5.4. De balansmethode (31 t/m 46)
5.5. Vergelijkingen oplossen (47 t/m 59)
5.6. Vergelijkingen toepassen (60 t/m 73)
5.1. Lineaire formules (1 t/m 12)
5.2. De richtingscoëfficiënt van een lijn (13 t/m 19)
5.3. De formule van een lijn opstellen (20 t/m 30)
5.4. De balansmethode (31 t/m 46)
5.5. Vergelijkingen oplossen (47 t/m 59)
5.6. Vergelijkingen toepassen (60 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


