TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 8.1 Inhoud prisma en cilinder VWO 2
Boek: Getal & Ruimte - Inhoud en vergroten VWO 2 (deel 2) opgaven 1 t/m 16, 2009Oppervlakte driehoek = 1/2 x basis x hoogte
Inhoud prisma = oppervlakte grondvlak x hoogte
Inhoud cilinder = oppervlakte grondcirkel x hoogte = π x straal2 x hoogte
Inhoud balk/kubus = lengte x breedte x hoogte
Inhoud prisma = oppervlakte grondvlak x hoogte
Inhoud cilinder = oppervlakte grondcirkel x hoogte = π x straal2 x hoogte
Inhoud balk/kubus = lengte x breedte x hoogte
1.
a. 60 cm3
b. 30 cm3
c. 6 cm2
d. ja
2.
b. Inhoud prisma = 40 cm3
c. Inhoud prisma = 36 cm3
3.
b. Inhoud prisma = 54 cm3
4.
5.
b. Hoogte garage is 3,9 meter.
c. Inhoud van de garage is 181,44 m3
6.
Inhoud doosje is 4760 mm3
7.
b. Schoonmaakkosten zijn ongeveer 1666 euro.
8.
a. In het zijkanaal past 35 000 liter water.
b. 3 minuten
9.
b. Inhoud van de doos is 145 cm3.
10.
b. 9 ml kan er nog bij.
a. 60 cm3
b. 30 cm3
c. 6 cm2
d. ja
2.
Tip:
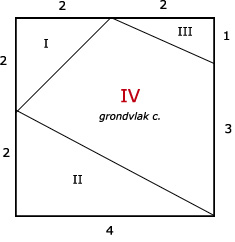
Bepaal eerst wat het grondvlak is en bereken dan de oppervlakte van het grondvlak. Vermenigvuldig deze dan met de hoogte. Bedenk: het grondvlak is NIET het rode vlak bij opgave 2. Bij vraag c. is oppervlakte grondvlak: IV = 16 - I - II - III.
a. Inhoud prisma = 32 cm3Bepaal eerst wat het grondvlak is en bereken dan de oppervlakte van het grondvlak. Vermenigvuldig deze dan met de hoogte. Bedenk: het grondvlak is NIET het rode vlak bij opgave 2. Bij vraag c. is oppervlakte grondvlak: IV = 16 - I - II - III.
b. Inhoud prisma = 40 cm3
c. Inhoud prisma = 36 cm3

3.
Tip:
Bij opgave 3 is het rode vlak WEL het grondvlak! De rest zijn altijd rechthoeken.
a. Inhoud prisma = 36 cm3Bij opgave 3 is het rode vlak WEL het grondvlak! De rest zijn altijd rechthoeken.
b. Inhoud prisma = 54 cm3
4.
Tip:
Het grondvlak bij de groentekas is een trapezium. Deze bestaat in dit geval uit een rechthoek van 2,8 x 2,4 en uit een driehoek. De hoogte van dit prisma is dan 1,5.
Inhoud groente kas is 11,8 m3.Het grondvlak bij de groentekas is een trapezium. Deze bestaat in dit geval uit een rechthoek van 2,8 x 2,4 en uit een driehoek. De hoogte van dit prisma is dan 1,5.
5.
Tip:
AD is de helft van 7,2.
a. De lengte van CD is 1,5 meter.AD is de helft van 7,2.
b. Hoogte garage is 3,9 meter.
c. Inhoud van de garage is 181,44 m3
6.
Inhoud doosje is 4760 mm3
7.
Tip:
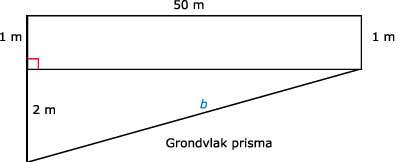
Bij opgave b. : bereken de blauwe b met de Stelling van Pythagoras en vermenigvuldig dit met 10 voor oppervlakte van de bodem.
a. Er kan in totaal 1 miljoen liter water in het zwembad.Bij opgave b. : bereken de blauwe b met de Stelling van Pythagoras en vermenigvuldig dit met 10 voor oppervlakte van de bodem.
b. Schoonmaakkosten zijn ongeveer 1666 euro.

8.
a. In het zijkanaal past 35 000 liter water.
b. 3 minuten
9.
Tip:
Bij a. bereken de oppervlakte van 3 balken (21 cm x 4 cm ) en 2 driehoeken. Bereken de hoogte van de driehoek (zijkant) met de Stelling van Pythagoras (h = hoogte driehoek = √12). Bij b. neem de oppervlakte van de driehoek (zijkant) x hoogte. De bijbehorende hoogte is 12.
a. Oppervlakte verpakking is 266 cm2.Bij a. bereken de oppervlakte van 3 balken (21 cm x 4 cm ) en 2 driehoeken. Bereken de hoogte van de driehoek (zijkant) met de Stelling van Pythagoras (h = hoogte driehoek = √12). Bij b. neem de oppervlakte van de driehoek (zijkant) x hoogte. De bijbehorende hoogte is 12.
b. Inhoud van de doos is 145 cm3.
10.
Tip:
Inhoud = oppervlakte grondvlak x hoogte. Straal is dus 5.
a. Inhoud ≈ 809 cm3. Dus er past 800 ml in.Inhoud = oppervlakte grondvlak x hoogte. Straal is dus 5.
b. 9 ml kan er nog bij.
11.
b. 100
c. Lengte strip is 188,5 cm.
12.
a. Er is 4,48 dm3 lood nodig voor de buis.
b. De buis bestaat uit 50,6 kg lood.
13.
a. 1325 cm3
b. 78,5% van de doos is gevuld.
14.
15.
16.
b. Als inhoud I en inhoud II gelijk zijn, dan heeft cilinder II een straal van √50. Dat is ongeveer 7,07.
Tip:
Bij c. bereken omtrek van een cirkel met diameter = 60.
a. Hoeveelheid dm3 staal is 9,3 dm3.Bij c. bereken omtrek van een cirkel met diameter = 60.
b. 100
c. Lengte strip is 188,5 cm.
12.
a. Er is 4,48 dm3 lood nodig voor de buis.
b. De buis bestaat uit 50,6 kg lood.
13.
a. 1325 cm3
b. 78,5% van de doos is gevuld.
14.
Tip:
Bepaal eerst de inhoud van de oorspronkelijke staaf (720π) en daarna de inhoud van een kleine staaf (16π). Deel deze op elkaar en je komt uit op 45.
Aantal staven is 45.Bepaal eerst de inhoud van de oorspronkelijke staaf (720π) en daarna de inhoud van een kleine staaf (16π). Deel deze op elkaar en je komt uit op 45.
15.
Tip:
Na 1 seconde heb je een buis van 3 meter gevuld met water. Na 1 minuut heb je een buis van 180 meter gevuld met water. Dat is 18 000 cm. Dus je krijgt een cilinder met h = 18 000 en r = 6.
Aantal liter door de buis is 2036 liter.Na 1 seconde heb je een buis van 3 meter gevuld met water. Na 1 minuut heb je een buis van 180 meter gevuld met water. Dat is 18 000 cm. Dus je krijgt een cilinder met h = 18 000 en r = 6.
16.
Tip:
Bij b. Stel Inhoud I = Inhoud II. Hieruit volgt: r2 = 300π / 6π = 50
a. Bereken Inhoud I met r = 5 en bereken Inhoud II met r = 10. Je ziet dat de inhouden dan niet gelijk zijn. Bij b. Stel Inhoud I = Inhoud II. Hieruit volgt: r2 = 300π / 6π = 50
b. Als inhoud I en inhoud II gelijk zijn, dan heeft cilinder II een straal van √50. Dat is ongeveer 7,07.
Andere paragrafen:
8.1. Inhoud prisma en cilinder (1 t/m 16)
8.2. Inhoud piramide en kegel (17 t/m 30)
8.3. Vergroten en verkleinen (31 t/m 39)
8.4. Oppervlakte bij vergroten (40 t/m 54)
8.5. Inhoud bij vergroten (55 t/m 70)
8.1. Inhoud prisma en cilinder (1 t/m 16)
8.2. Inhoud piramide en kegel (17 t/m 30)
8.3. Vergroten en verkleinen (31 t/m 39)
8.4. Oppervlakte bij vergroten (40 t/m 54)
8.5. Inhoud bij vergroten (55 t/m 70)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


