TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 4.4 Berekeningen met tangens HAVO 3
Boek: Getal & Ruimte - Aanzichten en hellingen HAVO 3 (deel 1) opgaven 37 t/m 56, 2010tangens van een hoek = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A
De tangens van hoek A schrijven we: tan(∠A).
Lees meer over de tangens
De tangens van hoek A schrijven we: tan(∠A).
Lees meer over de tangens
37.
a.
32º
b.
tan(∠B) = verticale verplaatsing / horizontale verplaatsing = AC / AB
tan(32º) = AC/6
AC = 6 x tan(32º)
AC ≈ 3,75
38.
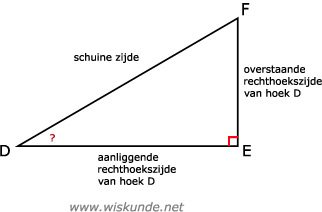
tan(∠D) = EF/DE
b.
tan(∠F) = DE/EF
39.
a.
∠A is scherp in de rechthoekige driehoek: ADC
tan(∠A) = CD/AD
b.
tan(∠B) = CD/BD
tan(∠C1) = AD/CD
tan(∠C2) = BD/CD
40.
tan(∠A1) = BC / AB
b.
tan(∠A2) = CD / AD
c.
tan(∠C1) = AD / CD
tan(∠C2) = AB / BC
41.
tan(∠B) = AC/AB = 5,3/4,1
∠B = tan-1(5,3/4,1)
∠B ≈ 52,3º
Manier 1: ∠C =>
tan(∠C) = AB/AC = 4,1/5,3
∠C = tan-1(4,1/5,3)
∠C ≈ 37,7º
of
Manier 2: ∠C =>
∠C = 180º - ∠A - ∠B
∠C = 180º - 90º - 52,3º
∠C = 37,7
42.
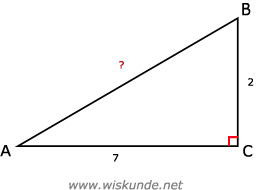
tan(∠A) = BC/AC = 2/7
∠A = tan-1(2/7)
∠A ≈ 15,9º
Manier 1: ∠B =>
tan(∠B) = AC/BC = 7/2
∠B = tan-1(7/2)
∠B ≈ 74,1º
of
Manier 2: ∠B =>
∠B = 180º - ∠C - ∠A
∠B = 180º - 90º - 15,9º
∠B = 74,1
43.
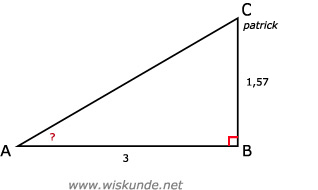
∠A = tan-1(1,57/3)
∠A ≈ 27,6º
Dus de zonnehoek is 27,6º.
44.
tan(∠B2) = 3/5
∠B2 = tan-1(3/5)
∠B2 ≈ 30,9º
tan(∠D2) = 3/2 = 1,5
∠D2 = tan-1(1,5)
∠D2 ≈ 56,3º
b.
tan(∠A1) = 2/3
∠A1 = tan-1(2/3)
∠A1 ≈ 33,69º
tan(∠A2) = 5/3
∠A2 = tan-1(5/3)
∠A2 ≈ 59,04º
∠A1 + ∠A2 = 33,69º + 59,4º = 92,7º
Dus de hoek is niet recht.
45.
tan(∠A) = verticale verplaatsing / horizontale verplaatsing = BC / AB
tan(∠A) = 8 / 6
∠A = tan-1(8 / 6)
∠A ≈ 53,1º
tan(∠D1) = verticale verplaatsing / horizontale verplaatsing = BC / BD
tan(∠D1) = 8 / 3
∠D1 = tan-1(8 / 3)
∠D1 ≈ 69,4º
b.
∠C2 = 180º - 90º - 69,4º = 20,6º
∠C12 = 180º - 90º - 53,1º = 36,9º
∠C1 = 36,9º - 20,6º = 16,3º
46.
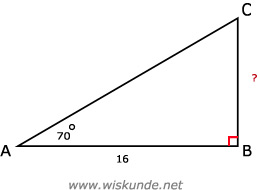
tan(70º) = BC/16
BC = tan(70º) x 16
BC ≈ 43,96
a.
32º
b.
tan(∠B) = verticale verplaatsing / horizontale verplaatsing = AC / AB
tan(32º) = AC/6
AC = 6 x tan(32º)
AC ≈ 3,75
38.
Tip:
De tangens kun je alleen gebruiken in een rechthoekige driehoek. Dat zie je aan de bekende (rode) winkelhaak.
a.De tangens kun je alleen gebruiken in een rechthoekige driehoek. Dat zie je aan de bekende (rode) winkelhaak.
tan(∠D) = EF/DE
b.
tan(∠F) = DE/EF

39.
a.
∠A is scherp in de rechthoekige driehoek: ADC
tan(∠A) = CD/AD
b.
tan(∠B) = CD/BD
tan(∠C1) = AD/CD
tan(∠C2) = BD/CD
40.
Tip:
Draai je boek steeds zo dat de 90 graden hoek en de gevraagde hoek op de "bodem" liggen. Dan zie je het beter.
a.Draai je boek steeds zo dat de 90 graden hoek en de gevraagde hoek op de "bodem" liggen. Dan zie je het beter.
tan(∠A1) = BC / AB
b.
tan(∠A2) = CD / AD
c.
tan(∠C1) = AD / CD
tan(∠C2) = AB / BC
41.
Tip:
De hoekensom van een driehoek is 180º.
∠B =>De hoekensom van een driehoek is 180º.
tan(∠B) = AC/AB = 5,3/4,1
∠B = tan-1(5,3/4,1)
∠B ≈ 52,3º
Manier 1: ∠C =>
tan(∠C) = AB/AC = 4,1/5,3
∠C = tan-1(4,1/5,3)
∠C ≈ 37,7º
of
Manier 2: ∠C =>
∠C = 180º - ∠A - ∠B
∠C = 180º - 90º - 52,3º
∠C = 37,7
42.
Tip:
Maak eerst een schets van de situatie.
∠A =>Maak eerst een schets van de situatie.
tan(∠A) = BC/AC = 2/7
∠A = tan-1(2/7)
∠A ≈ 15,9º
Manier 1: ∠B =>
tan(∠B) = AC/BC = 7/2
∠B = tan-1(7/2)
∠B ≈ 74,1º
of
Manier 2: ∠B =>
∠B = 180º - ∠C - ∠A
∠B = 180º - 90º - 15,9º
∠B = 74,1

43.
Tip:
10 tegels van 30x30 levert een schaduw AB van 10 x 30 is 3 meter.
tan(∠A) = BC/AB = 1,57/310 tegels van 30x30 levert een schaduw AB van 10 x 30 is 3 meter.
∠A = tan-1(1,57/3)
∠A ≈ 27,6º
Dus de zonnehoek is 27,6º.

44.
Tip:
Om aan te tonen of een hoek recht is, kun je ook kijken of de Stelling van Pythagoras klopt.
Dus of er links en rechts van het =-teken hetzelfde staat. Want dan moet de hoek wel 90º zijn.
a.Om aan te tonen of een hoek recht is, kun je ook kijken of de Stelling van Pythagoras klopt.
Dus of er links en rechts van het =-teken hetzelfde staat. Want dan moet de hoek wel 90º zijn.
tan(∠B2) = 3/5
∠B2 = tan-1(3/5)
∠B2 ≈ 30,9º
tan(∠D2) = 3/2 = 1,5
∠D2 = tan-1(1,5)
∠D2 ≈ 56,3º
b.
tan(∠A1) = 2/3
∠A1 = tan-1(2/3)
∠A1 ≈ 33,69º
tan(∠A2) = 5/3
∠A2 = tan-1(5/3)
∠A2 ≈ 59,04º
∠A1 + ∠A2 = 33,69º + 59,4º = 92,7º
Dus de hoek is niet recht.
45.
Tip:
De hoekensom van een driehoek is 180º
De hoekensom van een vierhoek is 360º
a.De hoekensom van een driehoek is 180º
De hoekensom van een vierhoek is 360º
tan(∠A) = verticale verplaatsing / horizontale verplaatsing = BC / AB
tan(∠A) = 8 / 6
∠A = tan-1(8 / 6)
∠A ≈ 53,1º
tan(∠D1) = verticale verplaatsing / horizontale verplaatsing = BC / BD
tan(∠D1) = 8 / 3
∠D1 = tan-1(8 / 3)
∠D1 ≈ 69,4º
b.
∠C2 = 180º - 90º - 69,4º = 20,6º
∠C12 = 180º - 90º - 53,1º = 36,9º
∠C1 = 36,9º - 20,6º = 16,3º
46.
Tip:
Zorg er altijd voor dat de hoek waar je mee werkt en de rechte hoek (90º) op "de bodem" liggen. Dan zie je het beter.
tan(∠A) = BC/ABZorg er altijd voor dat de hoek waar je mee werkt en de rechte hoek (90º) op "de bodem" liggen. Dan zie je het beter.
tan(70º) = BC/16
BC = tan(70º) x 16
BC ≈ 43,96

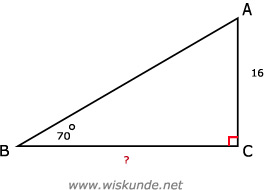
47.
tan(∠B) = AC/BC
tan(70º) = 16/BC
BC = 16 / tan(70º)
BC ≈ 5,8
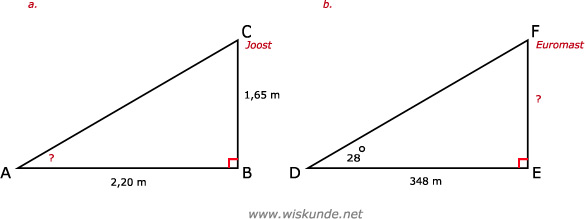
48.
tan(∠A) = BC/AB = 1,65/2,20
∠A = tan-1(1,65/2,20)
∠A ≈ 36,9º
Dus de zonnehoek is 36,9º.
b.
tan(∠D) = EF/DE
tan(28º) = EF/348
EF = tan(28º) x 348
EF ≈ 185,0
Dus de hoogte van de euromast is 185,0 meter.
49.
tan(65º) = AB/20
AB = 20 x tan(65º)
AB ≈ 42,89
AB ≈ 43 meter
Dus de breedte van het kanaal is 43 meter.
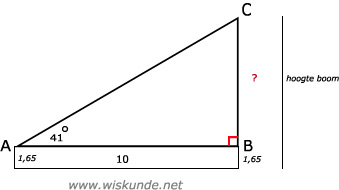
50.
tan(∠A) = BC/AB
tan(41º) = BC/10
BC = 10 x tan(41º)
BC ≈ 8,69
Dus de boom is 8,69 m + 1,65 m = 10,34 m.
51.
AB2 + AD2 = BD2
4,82 + 3,62 = BD2
BD2 = 36
BD = 6
tan(∠D) = BC/BD
tan(22º) = BC/6
BC = tan(22º) x 6
BC ≈ 2,42
CD nu met Pythagoras:
BC2 + BD2 = CD2
2,422 + 62 = CD2
CD2 = 41,8564
CD = √41,8564
CD ≈ 6,47
b.
tan(∠D2) = AB/AD = 4,8/3,6
∠D2 = tan-1(4,8/3,6)
∠D2 ≈ 53,1º
∠D12 = 22º + 53,1º = 75,1º
tan(∠D12) = AE/AD
tan(75,1º) = AE/3,6
AE = tan(75,1º) x 3,6
AE ≈ 13,53
52.
tan(∠C) = AB/AC
tan(52º) = 7/AC
AC = 7 / tan(52º)
AC ≈ 5,47
CD = AC - AD = 5,47 - 4 = 1,47
b.
tan(∠B1) = AD/AB = 4 / 7
∠B1 = tan-1(4 / 7)
∠B1 ≈ 29,7º
∠B12 = 180º - ∠C - ∠A
∠B12 = 180º - 52º - 90º
∠B12 = 38º
∠B2 = ∠B12 - ∠B1
∠B2 = 38º - 29,7º
∠B2 = 8,3º
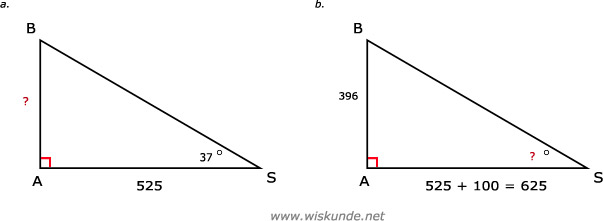
53.
tan(∠S) = AB/AS
tan(37º) = AB/525
AB = tan(37º) x 525
AB ≈ 395,62
Dus de lengte van het touw AB is 396 meter.
b.
tan(∠S) = AB/AS
tan(∠S) = 396/625
∠S = tan-1(396/625)
∠S ≈ 32,36 º
Dus de nieuwe hoek bij S is 32,4º.
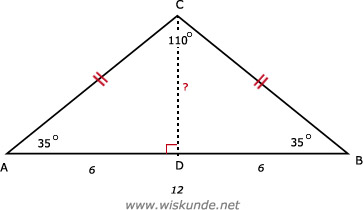
54.
Dus ∠A = 35º (de helft)
tan(∠A) = CD / AD
tan(35º) = CD / 6
CD = tan(35º) x 6
CD ≈ 4,20
Dus de hoogte CD die hoort bij zijde AB is 4,20.
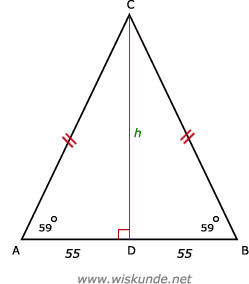
55.
tan(59º) = verticale verplaatsing / horizontale verplaatsing = h / 55
h = tan(59º) x 55
h = 91,5 cm
Afgerond op gehelen: 92 cm
b.
Bereken de lengte van AC.
AD2 + CD2 = AC2
552 + 922 = AC2
AC2 = 11 489
AC = √11 489
AC ≈ 107 cm
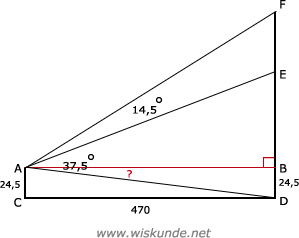
56.
tan(∠BAD) = BD/AB = 24,5/470
∠BAD = tan-1(24,5/470)
∠BAD ≈ 2,98º
∠BAE = 37,5º - 2,98º = 34,52º
Bereken nu BE met tan(∠BAE)
tan(∠BAE) = BE/AB
tan(34,52º) = BE/470
BE = 470 x tan(34,52º)
BE ≈ 323,26
Dus hoogte uitkijk platform (punt E) = 323,26 + 24,5 = 347,76 meter
b.
Bereken nu BF
tan(∠BAF) = BF/AB
tan(14,5º+34,52º) = BF/AB
tan(49,02º) = BF/470
BF = tan(49,02º) x 470
BF ≈ 541,05
Hoogte toren is BD + BF = 24,5 + 541,05 = 565,55
tan(∠B) = AC/BC
tan(70º) = 16/BC
BC = 16 / tan(70º)
BC ≈ 5,8

48.
Tip:
In een schets hoeven de afmetingen niet te kloppen. Daarom is het ook een schets.
a.In een schets hoeven de afmetingen niet te kloppen. Daarom is het ook een schets.
tan(∠A) = BC/AB = 1,65/2,20
∠A = tan-1(1,65/2,20)
∠A ≈ 36,9º
Dus de zonnehoek is 36,9º.
b.
tan(∠D) = EF/DE
tan(28º) = EF/348
EF = tan(28º) x 348
EF ≈ 185,0
Dus de hoogte van de euromast is 185,0 meter.

49.
Tip:
3 = 6 / 2 <=> 6 = 3 x 2
tan(∠C) = AB/AC3 = 6 / 2 <=> 6 = 3 x 2
tan(65º) = AB/20
AB = 20 x tan(65º)
AB ≈ 42,89
AB ≈ 43 meter
Dus de breedte van het kanaal is 43 meter.
50.
tan(∠A) = BC/AB
tan(41º) = BC/10
BC = 10 x tan(41º)
BC ≈ 8,69
Dus de boom is 8,69 m + 1,65 m = 10,34 m.

51.
Tip:
a. Bereken eerst BD met de Stelling van Pythagoras. Daarna kun je met de tangens BC berekenen.
b. Bereken eerst ∠D2 en neem daarna de tangens van ∠D12 (met AE).
a.a. Bereken eerst BD met de Stelling van Pythagoras. Daarna kun je met de tangens BC berekenen.
b. Bereken eerst ∠D2 en neem daarna de tangens van ∠D12 (met AE).
AB2 + AD2 = BD2
4,82 + 3,62 = BD2
BD2 = 36
BD = 6
tan(∠D) = BC/BD
tan(22º) = BC/6
BC = tan(22º) x 6
BC ≈ 2,42
CD nu met Pythagoras:
BC2 + BD2 = CD2
2,422 + 62 = CD2
CD2 = 41,8564
CD = √41,8564
CD ≈ 6,47
b.
tan(∠D2) = AB/AD = 4,8/3,6
∠D2 = tan-1(4,8/3,6)
∠D2 ≈ 53,1º
∠D12 = 22º + 53,1º = 75,1º
tan(∠D12) = AE/AD
tan(75,1º) = AE/3,6
AE = tan(75,1º) x 3,6
AE ≈ 13,53
52.
Tip:
Bij a: bereken eerst AC met de tangens. Dan CD = AC - AD.
Bij b: bereken eerst ∠B1 met de tangens en dan ∠B12. Dan weet je daarna ∠B2.
a.Bij a: bereken eerst AC met de tangens. Dan CD = AC - AD.
Bij b: bereken eerst ∠B1 met de tangens en dan ∠B12. Dan weet je daarna ∠B2.
tan(∠C) = AB/AC
tan(52º) = 7/AC
AC = 7 / tan(52º)
AC ≈ 5,47
CD = AC - AD = 5,47 - 4 = 1,47
b.
tan(∠B1) = AD/AB = 4 / 7
∠B1 = tan-1(4 / 7)
∠B1 ≈ 29,7º
∠B12 = 180º - ∠C - ∠A
∠B12 = 180º - 52º - 90º
∠B12 = 38º
∠B2 = ∠B12 - ∠B1
∠B2 = 38º - 29,7º
∠B2 = 8,3º
53.
Tip:
Bij a: Bereken de lengte van AB
Bij b: Bereken de nieuwe hoek bij S. AS wordt dus 100 meter langer.
a.Bij a: Bereken de lengte van AB
Bij b: Bereken de nieuwe hoek bij S. AS wordt dus 100 meter langer.
tan(∠S) = AB/AS
tan(37º) = AB/525
AB = tan(37º) x 525
AB ≈ 395,62
Dus de lengte van het touw AB is 396 meter.
b.
tan(∠S) = AB/AS
tan(∠S) = 396/625
∠S = tan-1(396/625)
∠S ≈ 32,36 º
Dus de nieuwe hoek bij S is 32,4º.

54.
Tip:
Gelijkbenige driehoek dus AC = BC en ∠A = ∠B
Bij een gelijkbenige driehoek zijn de basishoeken gelijk.
Voor ∠A en ∠B blijft over: 180º - 110º = 70ºGelijkbenige driehoek dus AC = BC en ∠A = ∠B
Bij een gelijkbenige driehoek zijn de basishoeken gelijk.
Dus ∠A = 35º (de helft)
tan(∠A) = CD / AD
tan(35º) = CD / 6
CD = tan(35º) x 6
CD ≈ 4,20
Dus de hoogte CD die hoort bij zijde AB is 4,20.

55.
Tip:
Maak een schets van de situatie.
AC is 1 van de 4 delen die even lang zijn.
AC kan met de Stelling van Pythagoras.
a.Maak een schets van de situatie.
AC is 1 van de 4 delen die even lang zijn.
AC kan met de Stelling van Pythagoras.
tan(59º) = verticale verplaatsing / horizontale verplaatsing = h / 55
h = tan(59º) x 55
h = 91,5 cm
Afgerond op gehelen: 92 cm
b.
Bereken de lengte van AC.
AD2 + CD2 = AC2
552 + 922 = AC2
AC2 = 11 489
AC = √11 489
AC ≈ 107 cm

56.
Tip:
Trek hulplijn AB en bereken eerst ∠BAD
a.Trek hulplijn AB en bereken eerst ∠BAD
tan(∠BAD) = BD/AB = 24,5/470
∠BAD = tan-1(24,5/470)
∠BAD ≈ 2,98º
∠BAE = 37,5º - 2,98º = 34,52º
Bereken nu BE met tan(∠BAE)
tan(∠BAE) = BE/AB
tan(34,52º) = BE/470
BE = 470 x tan(34,52º)
BE ≈ 323,26
Dus hoogte uitkijk platform (punt E) = 323,26 + 24,5 = 347,76 meter
b.
Bereken nu BF
tan(∠BAF) = BF/AB
tan(14,5º+34,52º) = BF/AB
tan(49,02º) = BF/470
BF = tan(49,02º) x 470
BF ≈ 541,05
Hoogte toren is BD + BF = 24,5 + 541,05 = 565,55

Andere paragrafen:
4.1. Aanzichten (1 t/m 11)
4.2. Hellingsgetal (12 t/m 20)
4.3. Tangens (21 t/m 36)
4.4. Berekeningen met tangens (37 t/m 56)
4.1. Aanzichten (1 t/m 11)
4.2. Hellingsgetal (12 t/m 20)
4.3. Tangens (21 t/m 36)
4.4. Berekeningen met tangens (37 t/m 56)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


