TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.2 Kwadratische formules VWO 2
Boek: Getal & Ruimte - Kwadraten en wortels VWO 2 (deel 1) opgaven 18 t/m 29, 2009Wat is een kwadratische formule?
Een kwadratische formule is een grafiek van de vorm: y = ax2 + bx + c. We noemen dit ook wel een parabool.
Om een parabool te tekenen, heb je 7 punten nodig. Een parabool heeft een symmetrieas door de top.
Voorbeelden van kwadratische formules: y = 3x2 + 2x + 1 of W = ½a2 - 6a + ¾
Als a > 0 dan hebben we te maken met een dalparabool. Is a < 0 dan is het een bergparabool.
Een kwadratische formule is een grafiek van de vorm: y = ax2 + bx + c. We noemen dit ook wel een parabool.
Om een parabool te tekenen, heb je 7 punten nodig. Een parabool heeft een symmetrieas door de top.
Voorbeelden van kwadratische formules: y = 3x2 + 2x + 1 of W = ½a2 - 6a + ¾
Als a > 0 dan hebben we te maken met een dalparabool. Is a < 0 dan is het een bergparabool.
18.
b. 25 - 68 = -43
c. 81 - 100 = -19
d. 36 + 6 - 32 + 3 = 13
e. 64 - 8 - 64 + 2 = -6
19.
a. Bij x = 3 hoort y = 15
b. Bij x = 0 hoort y = -3
c. Bij x = -4 hoort y = 29
20.
a. x = 3 invullen, levert y = (3)2 - 2 = 9 - 2 = 7
b. x = -3 invullen, levert y = (-3)2 - 2 = 9 - 2 = 7
c. x = -7 invullen, levert y = (-7)2 - 2 = 49 - 2 = 47
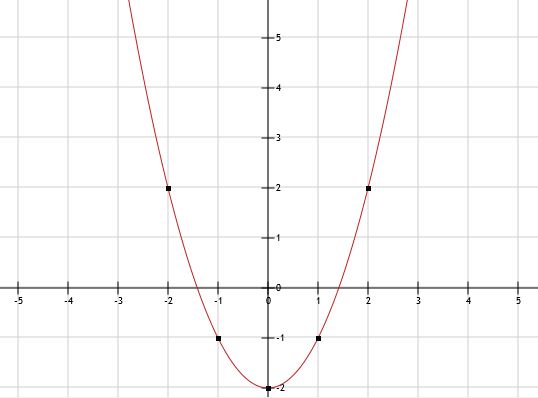
d.
e. Zie afbeelding
21.
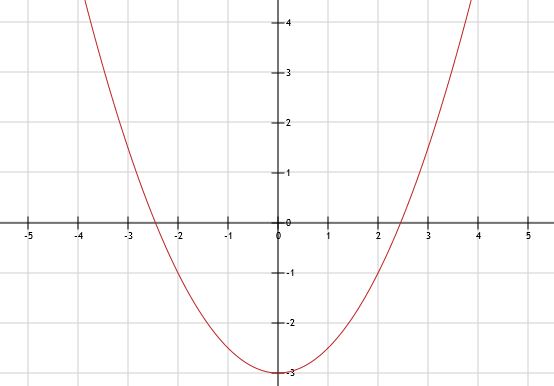
a. x = 3 invullen, levert y = 0,5 x (3)2 - 3 = 0,5 x 9 - 3 = 4,5 - 3 = 1,5
b. Zie afbeelding
c. Het is een dalparabool.
22.
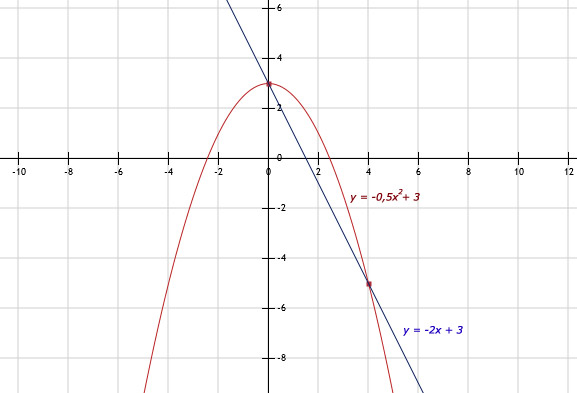
a. y = -0,5x2 + 3 is een parabool. De andere is een rechte lijn.
b. Zie afbeelding
c. De snijpunten zijn: (0,3) en (4,-5).
23.
a.
b. Het hoogste punt zit bij x = 0. De achtbaan is 21,6 meter hoog.
c. Bij x = 6 en x = -6 gaat de achtbaan in de grond. Afstand is 12 meter.
24.
b. Vul in x = 50 levert h(50) = 0,01 x 502 + 7 = 32. Dus de pylonen zijn 32 meter hoog.
c. 45 : 2 = 22,5. Vul in x = 22,5 levert h(22,5) = 0,01 x 22,52 + 7 = 12,0625. Dus de lampjes hangen op een hoogte van ca. 12 meter.
d. *
25.
Bij y = 0,5x2 hoort de rode grafiek.
Bij y = -x2 hoort de blauwe grafiek.
Bij y = -0,25x2 hoort de zwarte grafiek.
b. De dalparabolen zijn: II en IV
De bergparabolen zijn: I en III
26.
b. Het hoogste punt is de top. Dat is T(0,4).
c. Invullen x = 18 levert: -0,5 x (18)2 + 4 = -0,5 x 324 + 4 = -158
d. Invullen x = 26 levert: -0,5 x (26)2 + 4 = -0,5 x 676 + 4 = -334. Ja, punt ligt op de grafiek.
e. Invullen x = 6 levert: -0,5 x (6)2 + 4 = -0,5 x 36 + 4 = -14, dus dit punt ligt op de grafiek.
Invullen x = 16 levert: -0,5 x (16)2 + 4 = -0,5 x 256 + 4 = -124, dus dit punt ligt niet op de grafiek.
Invullen x = -5 levert: -0,5 x (-5)2 + 4 = -0,5 x 25 + 4 = -8,5, dus dit punt ligt op de grafiek.
Invullen x = -12 levert: -0,5 x (-12)2 + 4 = -0,5 x 144 + 4 = -68, dus dit punt ligt op de grafiek.
27.
b. Invullen x = 7 levert: y = 11,25, dus dit punt ligt op de grafiek.
Invullen x = 10 levert: y = 24, dus dit punt ligt niet op de grafiek.
Invullen x = -15 levert: y = 55,25, dus dit punt ligt op de grafiek.
Tip:
(-5)2 = -5 x -5 = 25
-52 = - 5 x 5 = -25
a. 36 - 20 = 16(-5)2 = -5 x -5 = 25
-52 = - 5 x 5 = -25
b. 25 - 68 = -43
c. 81 - 100 = -19
d. 36 + 6 - 32 + 3 = 13
e. 64 - 8 - 64 + 2 = -6
19.
a. Bij x = 3 hoort y = 15
b. Bij x = 0 hoort y = -3
c. Bij x = -4 hoort y = 29
20.
a. x = 3 invullen, levert y = (3)2 - 2 = 9 - 2 = 7
b. x = -3 invullen, levert y = (-3)2 - 2 = 9 - 2 = 7
c. x = -7 invullen, levert y = (-7)2 - 2 = 49 - 2 = 47
d.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 7 | 2 | -1 | -2 | -1 | 2 | 7 |
e. Zie afbeelding

21.
a. x = 3 invullen, levert y = 0,5 x (3)2 - 3 = 0,5 x 9 - 3 = 4,5 - 3 = 1,5
b. Zie afbeelding
c. Het is een dalparabool.

22.
a. y = -0,5x2 + 3 is een parabool. De andere is een rechte lijn.
b. Zie afbeelding
c. De snijpunten zijn: (0,3) en (4,-5).

23.
a.
| x | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
| h | 0 | 12 | 19,2 | 21,6 | 19,2 | 12 | 0 |
b. Het hoogste punt zit bij x = 0. De achtbaan is 21,6 meter hoog.
c. Bij x = 6 en x = -6 gaat de achtbaan in de grond. Afstand is 12 meter.
24.
Tip:
x is de afstand die je loopt vanaf de verticale lijn h naar links of rechts.
a. Vul in x = 0 levert h(0) = 0,01 x 02 + 7 = 7. Dus de weg is 7 meter boven het water.x is de afstand die je loopt vanaf de verticale lijn h naar links of rechts.
b. Vul in x = 50 levert h(50) = 0,01 x 502 + 7 = 32. Dus de pylonen zijn 32 meter hoog.
c. 45 : 2 = 22,5. Vul in x = 22,5 levert h(22,5) = 0,01 x 22,52 + 7 = 12,0625. Dus de lampjes hangen op een hoogte van ca. 12 meter.
d. *
25.
Tip:
Bij y = ax2 en a > 0 dan is het een dalparabool.
Bij y = ax2 en a < 0 dan is het een bergparabool.
a. Bij y = x2 hoort de groene grafiek.Bij y = ax2 en a > 0 dan is het een dalparabool.
Bij y = ax2 en a < 0 dan is het een bergparabool.
Bij y = 0,5x2 hoort de rode grafiek.
Bij y = -x2 hoort de blauwe grafiek.
Bij y = -0,25x2 hoort de zwarte grafiek.
b. De dalparabolen zijn: II en IV
De bergparabolen zijn: I en III
26.
Tip:
Om te bepalen of een punt P(x,y) op een parabool ligt, vul dit punt in en kijk of het klopt!
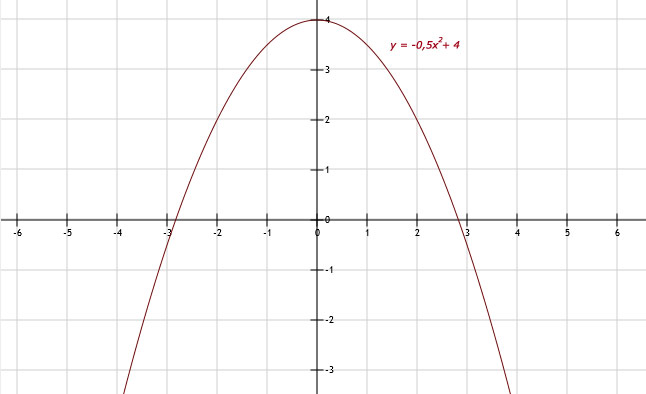
a.
Om te bepalen of een punt P(x,y) op een parabool ligt, vul dit punt in en kijk of het klopt!
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -0,5 | 2 | 3,5 | 4 | 3,5 | 2 | -0,5 |
b. Het hoogste punt is de top. Dat is T(0,4).
c. Invullen x = 18 levert: -0,5 x (18)2 + 4 = -0,5 x 324 + 4 = -158
d. Invullen x = 26 levert: -0,5 x (26)2 + 4 = -0,5 x 676 + 4 = -334. Ja, punt ligt op de grafiek.
e. Invullen x = 6 levert: -0,5 x (6)2 + 4 = -0,5 x 36 + 4 = -14, dus dit punt ligt op de grafiek.
Invullen x = 16 levert: -0,5 x (16)2 + 4 = -0,5 x 256 + 4 = -124, dus dit punt ligt niet op de grafiek.
Invullen x = -5 levert: -0,5 x (-5)2 + 4 = -0,5 x 25 + 4 = -8,5, dus dit punt ligt op de grafiek.
Invullen x = -12 levert: -0,5 x (-12)2 + 4 = -0,5 x 144 + 4 = -68, dus dit punt ligt op de grafiek.

27.
Tip:
Snijpunt y-as, dus x = 0, dus 0 invullen in de formule ofwel f(0).
a. Invullen x = 0 levert y = -1. Dus A(0,-1).Snijpunt y-as, dus x = 0, dus 0 invullen in de formule ofwel f(0).
b. Invullen x = 7 levert: y = 11,25, dus dit punt ligt op de grafiek.
Invullen x = 10 levert: y = 24, dus dit punt ligt niet op de grafiek.
Invullen x = -15 levert: y = 55,25, dus dit punt ligt op de grafiek.
28.
p = 0,25⋅(-4)2 - 1
p = 0,25⋅16 - 1
p = 4 - 1 = 3
p = 3
b. y = -3x2 + 8 door (5,q) levert:
q = -3⋅(5)2 + 8
q = -3⋅25 + 8
q = -67
c. y = ax2 door (2,8) levert:
8 = a⋅(2)2
8 = 4a
a = 2
d. y = -x2 + b door (-4,18) levert:
b = 34
29.
a. Bij t = 100 levert N = 250.
b. a = 0,025
c. t = 120 levert N = 0,025 x 1202 = 360
d. 1950 is t = 70. Dan N = 122,5. Antwoord:1,225 miljoen
Tip:
Is het getal voor de x2 positief dan is het een dalparabool.
Is het getal voor de x2 negatief dan is het een bergparabool.
a. y = 0,25x2 - 1 door (-4,p) levert:Is het getal voor de x2 positief dan is het een dalparabool.
Is het getal voor de x2 negatief dan is het een bergparabool.
p = 0,25⋅(-4)2 - 1
p = 0,25⋅16 - 1
p = 4 - 1 = 3
p = 3
b. y = -3x2 + 8 door (5,q) levert:
q = -3⋅(5)2 + 8
q = -3⋅25 + 8
q = -67
c. y = ax2 door (2,8) levert:
8 = a⋅(2)2
8 = 4a
a = 2
d. y = -x2 + b door (-4,18) levert:
b = 34
29.
a. Bij t = 100 levert N = 250.
b. a = 0,025
c. t = 120 levert N = 0,025 x 1202 = 360
d. 1950 is t = 70. Dan N = 122,5. Antwoord:1,225 miljoen
Andere paragrafen:
1.1. Rekenen met letters (1 t/m 17)
1.2. Kwadratische formules (18 t/m 29)
1.3. Wortels (30 t/m 44)
1.4. Wortels herleiden (45 t/m 57)
1.5. Het delen van wortels (58 t/m 64)
1.6. Allerlei soorten getallen (65 t/m 70)
1.1. Rekenen met letters (1 t/m 17)
1.2. Kwadratische formules (18 t/m 29)
1.3. Wortels (30 t/m 44)
1.4. Wortels herleiden (45 t/m 57)
1.5. Het delen van wortels (58 t/m 64)
1.6. Allerlei soorten getallen (65 t/m 70)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


