TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.3 Wortels VWO 2
Boek: Getal & Ruimte - Kwadraten en wortels VWO 2 (deel 1) opgaven 30 t/m 44, 2009De wortel is de zijde die hoort bij de oppervlakte van een vierkant.
Dus √3 is de zijde van een vierkant die een oppervlakte heeft van 3.
Stel een vierkant heeft een oppervlakte van 9. Wat is dan de lengte van de bijbehorende zijde?
De lengte van de zijde is dan √9 = 3. Dus de lengte van de zijde van een vierkant met oppervlakte 3 is dus √3.
De uitkomst van een wortel kan een mooi natuurlijk getal zijn maar ook een decimaal getal.
Enkele voorbeelden van mooie wortels zijn: √100 = 10, √81 = 9, √36 = 6, √4 = 2.
De wortel uit een negatief getal bestaat niet. Dus de √-16 kan niet!
Dus √3 is de zijde van een vierkant die een oppervlakte heeft van 3.
Stel een vierkant heeft een oppervlakte van 9. Wat is dan de lengte van de bijbehorende zijde?
De lengte van de zijde is dan √9 = 3. Dus de lengte van de zijde van een vierkant met oppervlakte 3 is dus √3.
De uitkomst van een wortel kan een mooi natuurlijk getal zijn maar ook een decimaal getal.
Enkele voorbeelden van mooie wortels zijn: √100 = 10, √81 = 9, √36 = 6, √4 = 2.
De wortel uit een negatief getal bestaat niet. Dus de √-16 kan niet!
30.
a. Oppervlakte tafelkleed is 1/2 x 22 = 2 m2.
b. 1,52 = 2,25. Omdat 2,25 meer is dan de werkelijke 2 m2.
c. 1,412 = 1,9881. Dus nog geen 2 m2. Want het tafelkleed is exact 2 m2.
d. Neem 1,41422 = 1,9999.. We komen steeds dichter bij. Maar wat is nu echt de waarde? Kijk verder!
31.
b. √279 ≈ 16,70
c. √279 ≈ 16,703
d. √279 ≈ 16,7033
32.
a. √17 ≈ 4,123
b. √28 ≈ 5,292
c. √62 ≈ 7,874
d. √0,03 ≈ 0,173
e. √1,82 ≈ 1,349
f. √38 759 ≈ 196,873
33.
b. 7,48
c. 0,94
d. 12,25
e. 12,35
f. 1,90
g. 19,44
h. 1,82
i. 9,79
34.
a. √20 ≈ 4,5
b. √8 ≈ 2,83. Dus afmetingen van de ruit zijn 2,83 m x 2,83 m.
35.
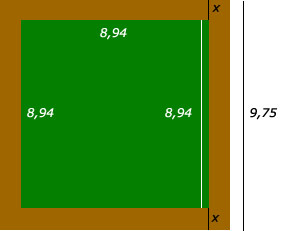
a. Zijde groen grasveld: √80 ≈ 8,94, dus afmetingen grasveld 8,94 m x 8,94 m.
b. Zijde bruin vierkant: √95 ≈ 9,75.
x + 8,94 + x = 9,75
2x + 8,94 = 9,75
2x = 0,81
x = 0,41. Dus breedte pad is 0,4 meter ofwel 40 cm.
36.
a. Oppervlakte 1 veld is 14/64 = 0,21875. Bijbehorende zijde is: √0,21875 ≈ 0,47.
b. Breedte van de rand is (4 - 3,74) / 2 = 0,13 dm.
37.
Succes met spelen!
38.
b. Het kwadraat van 12 is 144, dus √144 = 12.
39.
b. 7 + 9 = 16
c. √64 = 8
d. 3 x 5 + 5 x 1 = 15 + 5 = 20
e. 5 x 2 - 3 x 3 = 10 - 9 = 1
f. 2 x 7 - 12 = 14 - 12 = 2
a. Oppervlakte tafelkleed is 1/2 x 22 = 2 m2.
b. 1,52 = 2,25. Omdat 2,25 meer is dan de werkelijke 2 m2.
c. 1,412 = 1,9881. Dus nog geen 2 m2. Want het tafelkleed is exact 2 m2.
d. Neem 1,41422 = 1,9999.. We komen steeds dichter bij. Maar wat is nu echt de waarde? Kijk verder!
31.
Tip:
≈ betekent 'ongeveer'.
a. √279 ≈ 16,7≈ betekent 'ongeveer'.
b. √279 ≈ 16,70
c. √279 ≈ 16,703
d. √279 ≈ 16,7033
32.
a. √17 ≈ 4,123
b. √28 ≈ 5,292
c. √62 ≈ 7,874
d. √0,03 ≈ 0,173
e. √1,82 ≈ 1,349
f. √38 759 ≈ 196,873
33.
Tip:
Heeft een vierkant oppervlakte a dan is de lengte van de zijde van het vierkant √a.
a. 5,29Heeft een vierkant oppervlakte a dan is de lengte van de zijde van het vierkant √a.
b. 7,48
c. 0,94
d. 12,25
e. 12,35
f. 1,90
g. 19,44
h. 1,82
i. 9,79
34.
a. √20 ≈ 4,5
b. √8 ≈ 2,83. Dus afmetingen van de ruit zijn 2,83 m x 2,83 m.
35.
a. Zijde groen grasveld: √80 ≈ 8,94, dus afmetingen grasveld 8,94 m x 8,94 m.
b. Zijde bruin vierkant: √95 ≈ 9,75.
x + 8,94 + x = 9,75
2x + 8,94 = 9,75
2x = 0,81
x = 0,41. Dus breedte pad is 0,4 meter ofwel 40 cm.

36.
a. Oppervlakte 1 veld is 14/64 = 0,21875. Bijbehorende zijde is: √0,21875 ≈ 0,47.
b. Breedte van de rand is (4 - 3,74) / 2 = 0,13 dm.
37.
Succes met spelen!
38.
Tip:
Het kwadraat van a is a2, dus √a2 = a
a. Het kwadraat van 8 is 64, dus √64 = 8.Het kwadraat van a is a2, dus √a2 = a
b. Het kwadraat van 12 is 144, dus √144 = 12.
39.
Tip:
3⋅√25 = 3⋅5 = 15
a. 6 - 4 = 23⋅√25 = 3⋅5 = 15
b. 7 + 9 = 16
c. √64 = 8
d. 3 x 5 + 5 x 1 = 15 + 5 = 20
e. 5 x 2 - 3 x 3 = 10 - 9 = 1
f. 2 x 7 - 12 = 14 - 12 = 2
40.
a. 20 - 30 = -10
b. 3 x 4 + 14 = 12 + 14 = 26
c. 3 x 4 - 2 x 5 = 12 - 10 = 2
d. -5 x 6 + 2 x 9 = -30 + 18 = -12
e. 3 x 5 = 15
f. 5 x 13 - 144 = -79
41.
b. Mijn rekenmachine geeft ERROR!
c. Een kwadraat kan nooit negatief zijn.
42.
b. k.n.
c. -7
d. k.n.
e. √49 = 7
f. k.n.
g. k.n.
h. 0
i. 0
j. √16 x √81 = 4 x 9 = 36
43.
Dat is ongeveer 518 km/uur.
b. 3√d = 72
√d = 72/3 = 24 (nu links en rechts kwadrateren)
d = 242 = 576 (meter diep)
44.
a. Rompsnelheid is 17,0 knopen. Dat is 31,5 km/uur.
b. l = 42 levert r ≈ 15,878. Dat is 29,4 km/uur.
c. 2,45√l = 12, dus l = 24
a. 20 - 30 = -10
b. 3 x 4 + 14 = 12 + 14 = 26
c. 3 x 4 - 2 x 5 = 12 - 10 = 2
d. -5 x 6 + 2 x 9 = -30 + 18 = -12
e. 3 x 5 = 15
f. 5 x 13 - 144 = -79
41.
Tip:
√-4 bestaat niet! Want de oppervlakte van een vierkant kan nooit negatief zijn.
a. -3 x -3 = 9 en geen -9. Daarnaast de wortel uit een negatief getal bestaat niet.√-4 bestaat niet! Want de oppervlakte van een vierkant kan nooit negatief zijn.
b. Mijn rekenmachine geeft ERROR!
c. Een kwadraat kan nooit negatief zijn.
42.
Tip:
-√4 = -2, dus een min voor de wortel kan wel. Zolang er onder de wortel maar een positief getal staat.
a. 7-√4 = -2, dus een min voor de wortel kan wel. Zolang er onder de wortel maar een positief getal staat.
b. k.n.
c. -7
d. k.n.
e. √49 = 7
f. k.n.
g. k.n.
h. 0
i. 0
j. √16 x √81 = 4 x 9 = 36
43.
Tip:
1 km = 1000 m van m/s naar km/u -> maal 3,6
a. d = 2300 levert v = 3⋅√2300 ≈ 143,87 m/s.1 km = 1000 m van m/s naar km/u -> maal 3,6
Dat is ongeveer 518 km/uur.
b. 3√d = 72
√d = 72/3 = 24 (nu links en rechts kwadrateren)
d = 242 = 576 (meter diep)
44.
a. Rompsnelheid is 17,0 knopen. Dat is 31,5 km/uur.
b. l = 42 levert r ≈ 15,878. Dat is 29,4 km/uur.
c. 2,45√l = 12, dus l = 24
Andere paragrafen:
1.1. Rekenen met letters (1 t/m 17)
1.2. Kwadratische formules (18 t/m 29)
1.3. Wortels (30 t/m 44)
1.4. Wortels herleiden (45 t/m 57)
1.5. Het delen van wortels (58 t/m 64)
1.6. Allerlei soorten getallen (65 t/m 70)
1.1. Rekenen met letters (1 t/m 17)
1.2. Kwadratische formules (18 t/m 29)
1.3. Wortels (30 t/m 44)
1.4. Wortels herleiden (45 t/m 57)
1.5. Het delen van wortels (58 t/m 64)
1.6. Allerlei soorten getallen (65 t/m 70)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


