TIP: Wil je ook toegang tot meer dan 16.900 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 9B.4 Ongelijkheden grafisch oplossen HAVO 3
Boek: Getal & Ruimte - Vergelijkingen en ongelijkheden HAVO 3 (deel 2) opgaven 29 t/m 37, 2010Hoe lossen we de ongelijkheid f(x) < g(x) grafisch op?
Gegeven 2 functies. Bijvoorbeeld f(x) is een dalparabool en g(x) is een rechte lijn.
Dan vragen we ons af: voor welke x-waarden ligt de parabool onder de lijn?
Bepaal eerst de snijpunten door op te lossen waar de functies aan elkaar gelijk zijn: f(x) = g(x).
Teken beide functies in een assenstelsel en kleur het gedeelte van de x-as waar de parabool onder de lijn ligt.
Schrijf je antwoord op.
Gegeven 2 functies. Bijvoorbeeld f(x) is een dalparabool en g(x) is een rechte lijn.
Dan vragen we ons af: voor welke x-waarden ligt de parabool onder de lijn?
Bepaal eerst de snijpunten door op te lossen waar de functies aan elkaar gelijk zijn: f(x) = g(x).
Teken beide functies in een assenstelsel en kleur het gedeelte van de x-as waar de parabool onder de lijn ligt.
Schrijf je antwoord op.
29.
a. -3 < x < 4
b. 0 < x < 20
c. 2 1/2 < x < 3 1/4
30.
a. x < -2 v x > 5
b. x < -7 v x > -3
c. x < 0 v x > 8
31.
a. -1 < x < 3
b. x < -5 v x > 4
c. x > -5
d. x < 5 v x > 9
e. -5 < x < 6
f. x > -4
32.
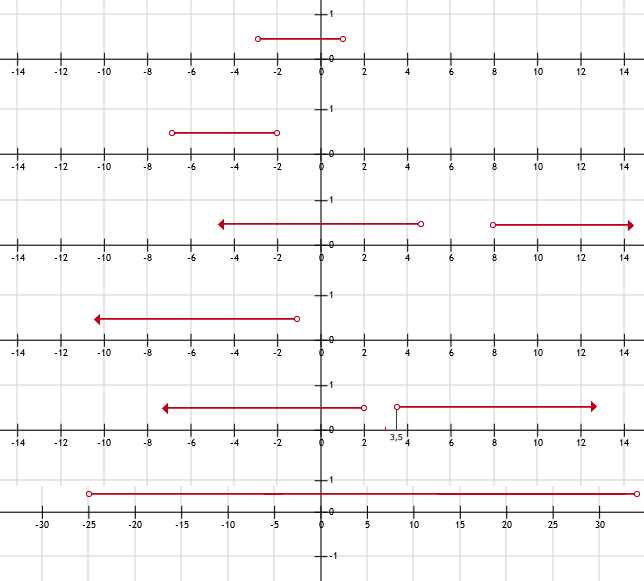
33.
a. Buiten warmer dan binnen van 12:00 tot 16:00.
b. Binnen 4 graden warmer dan buiten om 09:30.
c. Van 08:00 tot 11:00 en van 18:00 tot 20:00. Dat is gedurende 5 uur.
34.
a.g(5) = 4
b. f(0) = 4, g(0) = 8, f(1) = 6, g(1) = 6, f(2) = 8, g(2) = 4
c. Bij x = 2 ligt de grafiek van f boven de grafiek van g, dus f(2) > g(2).
Bij x = 4 ligt de grafiek van f boven de grafiek van g, dus f(4) > g(4).
Bij x = 7 ligt de grafiek van f onder de grafiek van g, dus f(7) < g(7).
d. Bij x = 4 ligt de grafiek van f boven de grafiek van g.
e. x = 3 is een oplossing van f(x) > g(x).
x = 8 is geen oplossing van f(x) > g(x).
f. De x-waarden (op de x-as) tussen 1 en 6 zijn de oplossingen van f(x) > g(x). We noteren dat als: 1 < x < 6.
35.
Waar ligt f onder g? -> f(x) < g(x) levert x < 1 v x > 6
b. Wat zijn de snijpunten van h(x) = k(x)? Dat is bij x = -1 of x = 5
Waar ligt h boven k? -> h(x) > k(x) levert -1 < x < 5
c. Wat zijn de snijpunten van l(x) = m(x)? Dat is bij x = 0 of x = 5
Waar ligt l boven m? -> l(x) > m(x) levert x < 0 v x > 5
36.
a. Wat zijn de snijpunten van f(x) = g(x)? Dat is bij x = 1 of x = 6
Waar ligt f onder g? -> f(x) < g(x) levert x < 1 v x > 6
b. Wat zijn de snijpunten van h(x) = k(x)? Dat is bij x = -4 of x = 2
Waar ligt h boven k? -> h(x) > k(x) levert -4 < x < 2
c. Wat zijn de snijpunten van l(x) = m(x)? Dat is bij x = 0 of x = 5
Waar ligt l boven m? -> l(x) > m(x) levert x < 0 v x > 5
37.
a. Wat zijn de snijpunten van g(x) = 3? Dat is bij x = 0 of x = 6
Waar ligt g boven y = 3? -> g(x) > 3 levert 0 < x < 6
b. Wat zijn de snijpunten van h(x) = -1? Dat is bij x = -2 of x = 5
Waar ligt h onder y = -1? -> h(x) < -1 levert x < -2 v x > 5
c. Wat zijn de snijpunten van k(x) = 2? Dat is bij x = 2 of x = 7
Waar ligt k onder y = 2? -> k(x) < 2 levert 2 < x < 7
a. -3 < x < 4
b. 0 < x < 20
c. 2 1/2 < x < 3 1/4
30.
a. x < -2 v x > 5
b. x < -7 v x > -3
c. x < 0 v x > 8
31.
a. -1 < x < 3
b. x < -5 v x > 4
c. x > -5
d. x < 5 v x > 9
e. -5 < x < 6
f. x > -4
32.
Tip:
Als we ≤ of ≥ zouden gebruiken dan moeten de 'rode ring bolletjes' dicht zijn.
Zie afbeeldingAls we ≤ of ≥ zouden gebruiken dan moeten de 'rode ring bolletjes' dicht zijn.

33.
a. Buiten warmer dan binnen van 12:00 tot 16:00.
b. Binnen 4 graden warmer dan buiten om 09:30.
c. Van 08:00 tot 11:00 en van 18:00 tot 20:00. Dat is gedurende 5 uur.
34.
a.g(5) = 4
b. f(0) = 4, g(0) = 8, f(1) = 6, g(1) = 6, f(2) = 8, g(2) = 4
c. Bij x = 2 ligt de grafiek van f boven de grafiek van g, dus f(2) > g(2).
Bij x = 4 ligt de grafiek van f boven de grafiek van g, dus f(4) > g(4).
Bij x = 7 ligt de grafiek van f onder de grafiek van g, dus f(7) < g(7).
d. Bij x = 4 ligt de grafiek van f boven de grafiek van g.
e. x = 3 is een oplossing van f(x) > g(x).
x = 8 is geen oplossing van f(x) > g(x).
f. De x-waarden (op de x-as) tussen 1 en 6 zijn de oplossingen van f(x) > g(x). We noteren dat als: 1 < x < 6.
35.
Tip:
Bepaal eerst de x-coördinaten van de snijpunten van de grafieken.
a.
Wat zijn de snijpunten van f(x) = g(x)? Dat is bij x = 1 of x = 6Bepaal eerst de x-coördinaten van de snijpunten van de grafieken.
Waar ligt f onder g? -> f(x) < g(x) levert x < 1 v x > 6
b. Wat zijn de snijpunten van h(x) = k(x)? Dat is bij x = -1 of x = 5
Waar ligt h boven k? -> h(x) > k(x) levert -1 < x < 5
c. Wat zijn de snijpunten van l(x) = m(x)? Dat is bij x = 0 of x = 5
Waar ligt l boven m? -> l(x) > m(x) levert x < 0 v x > 5
36.
a. Wat zijn de snijpunten van f(x) = g(x)? Dat is bij x = 1 of x = 6
Waar ligt f onder g? -> f(x) < g(x) levert x < 1 v x > 6
b. Wat zijn de snijpunten van h(x) = k(x)? Dat is bij x = -4 of x = 2
Waar ligt h boven k? -> h(x) > k(x) levert -4 < x < 2
c. Wat zijn de snijpunten van l(x) = m(x)? Dat is bij x = 0 of x = 5
Waar ligt l boven m? -> l(x) > m(x) levert x < 0 v x > 5
37.
a. Wat zijn de snijpunten van g(x) = 3? Dat is bij x = 0 of x = 6
Waar ligt g boven y = 3? -> g(x) > 3 levert 0 < x < 6
b. Wat zijn de snijpunten van h(x) = -1? Dat is bij x = -2 of x = 5
Waar ligt h onder y = -1? -> h(x) < -1 levert x < -2 v x > 5
c. Wat zijn de snijpunten van k(x) = 2? Dat is bij x = 2 of x = 7
Waar ligt k onder y = 2? -> k(x) < 2 levert 2 < x < 7
Andere paragrafen:
9B.1. Herleiden (1 t/m 10)
9B.2. Vergelijkingen (11 t/m 21)
9B.3. Lineaire ongelijkheden (22 t/m 28)
9B.4. Ongelijkheden grafisch oplossen (29 t/m 37)
9B.5. Kwadratische ongelijkheden (38 t/m 42)
9B.1. Herleiden (1 t/m 10)
9B.2. Vergelijkingen (11 t/m 21)
9B.3. Lineaire ongelijkheden (22 t/m 28)
9B.4. Ongelijkheden grafisch oplossen (29 t/m 37)
9B.5. Kwadratische ongelijkheden (38 t/m 42)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


