TIP: Wil je ook toegang tot meer dan 17.800 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.5 Vierhoeken VMBO 2 KGT
Boek: Getal & Ruimte - Vlakke figuren VMBO 2 (deel 1) opgaven 58 t/m 76, 2009Vierhoeken hebben bijzondere eigenschappen. Voorbeelden van bijzondere vierhoeken zijn:
- Parallellogram
- Ruit
- Trapezium
- Vlieger
Een trapezium kan ook rechthoekig of gelijkbenig zijn.
- Parallellogram
- Ruit
- Trapezium
- Vlieger
Een trapezium kan ook rechthoekig of gelijkbenig zijn.
58.
a. *
b. Een rechthoek is vouwsymmetrisch en draaisymmetrisch.
c. *
d. Een parallellogram is niet vouwsymmetrisch maar wel draaisymmetrisch. De kleinste draaihoek is 180º.
e. Ja, de overstaande zijden van een rechthoek zijn evenwijdig.
f. Ja, de overstaande zijden van een parallellogram zijn evenwijdig.
g. Ja, de overstaande zijden van een rechthoek zijn even lang.
h. Ja, de overstaande zijden van een parallellogram zijn even lang.
i. Een verschil is dat een rechthoek wel 4 rechte hoeken heeft en een parallellogram niet.
59.
a. Even grote hoeken zijn: ∠A2 = ∠B2 = ∠C2 = ∠D2 en tevens ∠A2 = ∠A4 = ∠B4 = ∠C4 = ∠D4
b. Ja, in een parallellogram zijn overstaande hoeken even groot.
c. Ja, zie b.
60.
b. *
c. *
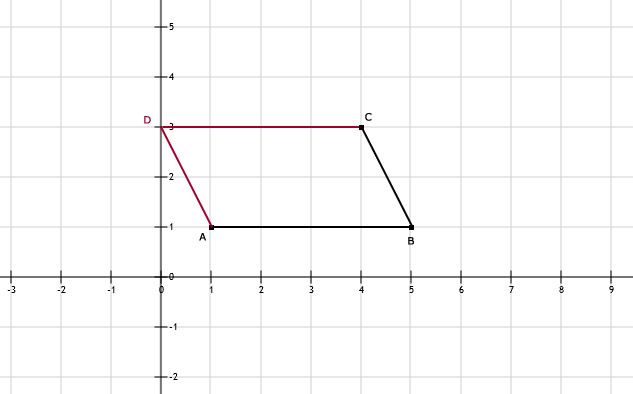
61.
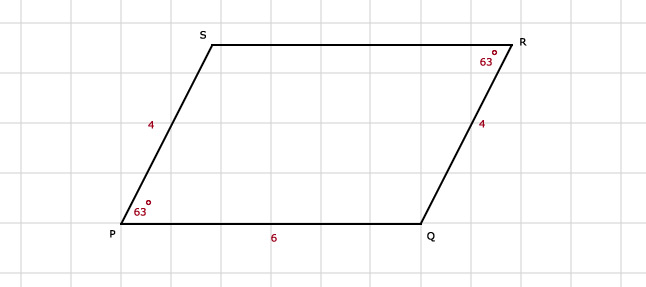
62.
a. *
b. Een vierkant heeft 4 symmetrieassen.
c. Een vierkant is draaisymmetrisch (minimale draaihoek is 90º).
63.
b. Een ruit heeft 2 symmetrieassen.
c. Een ruit is draaisymmetrisch (minimale draaihoek is 180º).
64.
a. Ja, alle zijden van een vierkant zijn even lang.
b. Ja, alle zijden van een ruit zijn even lang.
c. Ja, de overstaande zijden van een vierkant zijn evenwijdig.
d. Ja, de overstaande zijden van een ruit zijn evenwijdig.
65.
a. Een vierkant heeft 4 rechte hoeken, een ruit niet.
b. Bij een ruit staan de diagonalen loodrecht op elkaar, bij een parallellogram niet.
66.
a. Zie afbeelding
b. *
c. *
d. *
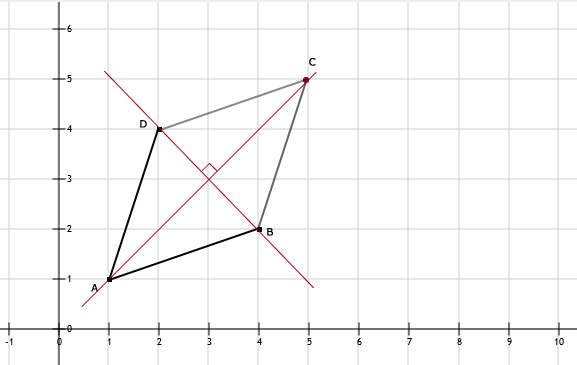
67.
Zie afbeelding
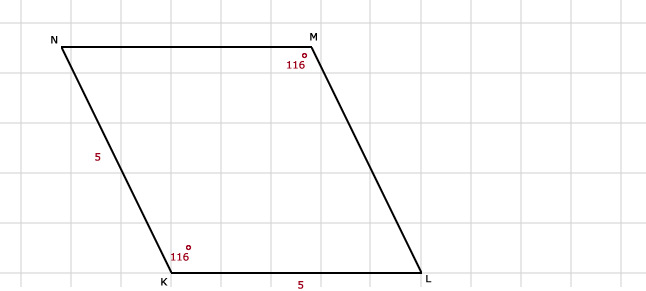
a. *
b. Een rechthoek is vouwsymmetrisch en draaisymmetrisch.
c. *
d. Een parallellogram is niet vouwsymmetrisch maar wel draaisymmetrisch. De kleinste draaihoek is 180º.
e. Ja, de overstaande zijden van een rechthoek zijn evenwijdig.
f. Ja, de overstaande zijden van een parallellogram zijn evenwijdig.
g. Ja, de overstaande zijden van een rechthoek zijn even lang.
h. Ja, de overstaande zijden van een parallellogram zijn even lang.
i. Een verschil is dat een rechthoek wel 4 rechte hoeken heeft en een parallellogram niet.
59.
a. Even grote hoeken zijn: ∠A2 = ∠B2 = ∠C2 = ∠D2 en tevens ∠A2 = ∠A4 = ∠B4 = ∠C4 = ∠D4
b. Ja, in een parallellogram zijn overstaande hoeken even groot.
c. Ja, zie b.
60.
Tip:
In een parallellogram zijn overstaande zijden evenwijdig.
a. Zie afbeeldingIn een parallellogram zijn overstaande zijden evenwijdig.
b. *
c. *

61.
Tip:
In een parallellogram zijn overstaande hoeken even groot en overstaande zijden evenwijdig.
Zie afbeeldingIn een parallellogram zijn overstaande hoeken even groot en overstaande zijden evenwijdig.

62.
a. *
b. Een vierkant heeft 4 symmetrieassen.
c. Een vierkant is draaisymmetrisch (minimale draaihoek is 90º).
63.
Tip:
Eigenschappen van een ruit: Overstaande hoeken zijn even groot, alle zijden zijn even lang, de diagonalen delen elkaar loodrecht middendoor, er zijn 2 symmetrieassen, draaisymmetrisch over 180º
a. *Eigenschappen van een ruit: Overstaande hoeken zijn even groot, alle zijden zijn even lang, de diagonalen delen elkaar loodrecht middendoor, er zijn 2 symmetrieassen, draaisymmetrisch over 180º
b. Een ruit heeft 2 symmetrieassen.
c. Een ruit is draaisymmetrisch (minimale draaihoek is 180º).
64.
a. Ja, alle zijden van een vierkant zijn even lang.
b. Ja, alle zijden van een ruit zijn even lang.
c. Ja, de overstaande zijden van een vierkant zijn evenwijdig.
d. Ja, de overstaande zijden van een ruit zijn evenwijdig.
65.
a. Een vierkant heeft 4 rechte hoeken, een ruit niet.
b. Bij een ruit staan de diagonalen loodrecht op elkaar, bij een parallellogram niet.
66.
a. Zie afbeelding
b. *
c. *
d. *

67.
Zie afbeelding

68.
a. De symmetrieas van de vlieger loopt door BD.
b. Ja, want BD is een spiegellijn.
c. Nee
d. Nee, de diagonalen bij een vlieger zijn niet even lang.
69.
b. Een vlieger is niet draaisymmetrisch.
70.
a. Zie afbeelding
b. *
c. Nee, de diagonalen zijn niet even lang.
d. Omdat AD en BC niet even lang zijn.
71.
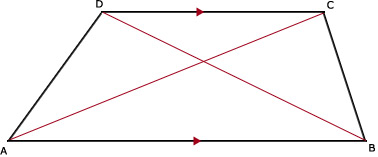
a. Zie afbeelding
b. *
c. Ja, de vierhoek is een trapezium omdat AD en BC evenwijdig zijn.
d. Ja, het is een rechthoekig trapezium omdat hoek B een rechte hoek is.
72.
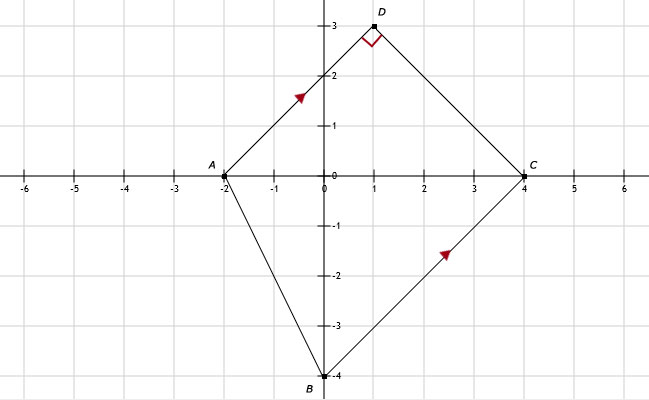
b. Ja, de hoeken passen op elkaar. Want de symmetrieas zorgt daarvoor.
c. ∠S = ∠R
73.
Sorry, ik heb helaas geen werkboek
74.
*
75.
*
76.
a. 3 verschillen tussen een ruit en een rechthoek zijn:
1. Een rechthoek heeft 4 rechte hoeken, een ruit niet.
2. Een ruit heeft 4 gelijke zijden, een rechthoek niet.
3. Bij een ruit staan de diagonalen loodrecht op elkaar, bij een rechthoek niet.
b. Een ruit heeft 2 symmetrieassen, een vierkant 4 en een rechthoek 2.
a. De symmetrieas van de vlieger loopt door BD.
b. Ja, want BD is een spiegellijn.
c. Nee
d. Nee, de diagonalen bij een vlieger zijn niet even lang.
69.
Tip:
Eigenschappen van een vlieger: Twee overstaande hoeken zijn even groot, zijden zijn twee aan twee even lang, de diagonalen delen elkaar loodrecht middendoor, er is 1 symmetrieas, niet draaisymmetrisch, niet puntsymmetrisch.
a. AB en BC zijn even lang en AD en CD zijn even lang.Eigenschappen van een vlieger: Twee overstaande hoeken zijn even groot, zijden zijn twee aan twee even lang, de diagonalen delen elkaar loodrecht middendoor, er is 1 symmetrieas, niet draaisymmetrisch, niet puntsymmetrisch.
b. Een vlieger is niet draaisymmetrisch.
70.
a. Zie afbeelding
b. *
c. Nee, de diagonalen zijn niet even lang.
d. Omdat AD en BC niet even lang zijn.

71.
a. Zie afbeelding
b. *
c. Ja, de vierhoek is een trapezium omdat AD en BC evenwijdig zijn.
d. Ja, het is een rechthoekig trapezium omdat hoek B een rechte hoek is.

72.
Tip:
Een symmetrieas noemen we ook wel een spiegelas.
a. Teken een lijn door het midden van PQ en het midden van RS. Dit is de symmetrieas.Een symmetrieas noemen we ook wel een spiegelas.
b. Ja, de hoeken passen op elkaar. Want de symmetrieas zorgt daarvoor.
c. ∠S = ∠R
73.
Sorry, ik heb helaas geen werkboek
74.
*
75.
*
76.
a. 3 verschillen tussen een ruit en een rechthoek zijn:
1. Een rechthoek heeft 4 rechte hoeken, een ruit niet.
2. Een ruit heeft 4 gelijke zijden, een rechthoek niet.
3. Bij een ruit staan de diagonalen loodrecht op elkaar, bij een rechthoek niet.
b. Een ruit heeft 2 symmetrieassen, een vierkant 4 en een rechthoek 2.
Andere paragrafen:
1.1. Eigenschappen van vlakke figuren (1 t/m 14)
1.2. Namen van vlakke figuren (15 t/m 22)
1.3. Driehoeken (23 t/m 39)
1.4. Driehoeken tekenen (40 t/m 57)
1.5. Vierhoeken (58 t/m 76)
1.6. Hoeken berekenen in een vierhoek (77 t/m 88)
1.1. Eigenschappen van vlakke figuren (1 t/m 14)
1.2. Namen van vlakke figuren (15 t/m 22)
1.3. Driehoeken (23 t/m 39)
1.4. Driehoeken tekenen (40 t/m 57)
1.5. Vierhoeken (58 t/m 76)
1.6. Hoeken berekenen in een vierhoek (77 t/m 88)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


