TIP: Wil je ook toegang tot meer dan 17.800 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.6 Hoeken berekenen in een vierhoek VMBO 2 KGT
Boek: Getal & Ruimte - Vlakke figuren VMBO 2 (deel 1) opgaven 77 t/m 88, 2009Enkele hulpmiddelen bij het berekenen van hoeken:
- Overstaande hoeken zijn even groot.
- Een gestrekte hoek is een hoek van 180 graden.
- De hoekensom van een driehoek is 180 graden.
- De hoekensom van een vierhoek is 360 graden.
- Overstaande hoeken zijn even groot.
- Een gestrekte hoek is een hoek van 180 graden.
- De hoekensom van een driehoek is 180 graden.
- De hoekensom van een vierhoek is 360 graden.
77.
a. De overstaande hoek van ∠A1 is ∠A3.
b. De overstaande hoek van ∠A4 is ∠A2.
c. Een gestrekte hoek is 180º.
d. ∠A1 + ∠A4 = 180º
e. ∠A1 + ∠A2 = 180º
78.
b. ∠B4 = 180º - 80º = 100º (samen een gestrekte hoek)
c. ∠B2 = ∠B4 = 100º (overstaande hoeken)
79.
a. ∠B1 = 55º
∠B2 = 180º - 55º = 125º (samen een gestrekte hoek)
∠B3 = ∠B1 = 55º (overstaande hoeken)
∠B4 = ∠B2 = 125º (overstaande hoeken)
b. ∠B1 past op de hoeken: ∠A1 en ∠C1 en ∠D1
c. ∠D3 = ∠B3 = 55º
d. ∠A2 = ∠B2 = 125º
e. ∠C4 = ∠B4 = 125º
80.
b. ∠P2 = ∠S2 = 128º
c. ∠Q1 = ∠S1 = ∠S3 = 52º
d. ∠S3 + ∠P2 + ∠Q1 + ∠R4 =
52º + 128º + 52º + 128º = 360º
81.
a. ∠K2 = ∠L2 (passen op elkaar)
∠L2 = 180º - 123º = 57º (samen een gestrekte hoek)
Dus: ∠K2 = 57º
b. ∠N4 = ∠L4 (passen op elkaar)
∠L4 = ∠L1 = 123º (overstaande hoeken)
Dus: ∠N4 = 123º
c. ∠M3 = ∠M2 (overstaande hoeken)
∠M2 = ∠L2 = (passen op elkaar)
Dus: ∠M3 = 57º
d. Samen zijn de hoeken van een vierhoek (en dus ook van een ruit) 360º.
82.
a. Teken een lijn door het midden van AB en het midden van CD. Dit is de symmetrieas. (zie afbeelding)
b. Ja, ∠A2 = ∠B1 (ivm symmetrieas / spiegelas)
c. ∠A2 past op ∠D2
d. ∠D4 past op ∠A4
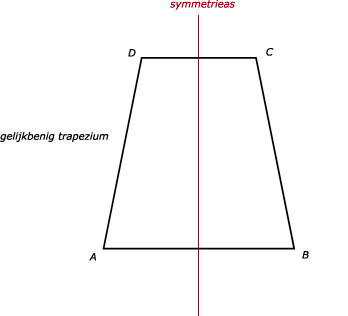
83.
a.
∠A1 = 180º - 62º = 118º (samen een gestrekte hoek)
∠A2 = 62º (is gegeven)
∠A3 = ∠A2 = 62º (overstaande hoeken)
∠A4 = ∠A1 = 118º (overstaande hoeken)
Alle hoeken bij D zijn gelijk aan de hoeken bij A. Want deze passen op elkaar na verschuiven.
∠B1 = ∠A2 = 62º (symmetrieas)
∠B2 = 180º - 62º = 118º (samen een gestrekte hoek)
∠B3 = ∠B2 = 118º (overstaande hoeken)
∠B4 = ∠B1 = 62º (overstaande hoeken)
Alle hoeken bij C zijn gelijk aan de hoeken bij B. Want deze passen op elkaar na verschuiven.
b. Samen zijn de hoeken van een vierhoek (en dus ook van een trapezium) 360º.
84.
a. Ja, deze diagonaal is ook de symmetrieas van de vlieger.
b. ∠D past op ∠B
c. ∠A1 past op ∠A2
d. ∠C1 past op ∠C2
85.
b. 180 graden
c. 360 graden
86.
∠Q = 85º
a. De overstaande hoek van ∠A1 is ∠A3.
b. De overstaande hoek van ∠A4 is ∠A2.
c. Een gestrekte hoek is 180º.
d. ∠A1 + ∠A4 = 180º
e. ∠A1 + ∠A2 = 180º
78.
Tip:
Overstaande hoeken zijn even groot.
a. ∠B1 = ∠B3 = 80ºOverstaande hoeken zijn even groot.
b. ∠B4 = 180º - 80º = 100º (samen een gestrekte hoek)
c. ∠B2 = ∠B4 = 100º (overstaande hoeken)
79.
a. ∠B1 = 55º
∠B2 = 180º - 55º = 125º (samen een gestrekte hoek)
∠B3 = ∠B1 = 55º (overstaande hoeken)
∠B4 = ∠B2 = 125º (overstaande hoeken)
b. ∠B1 past op de hoeken: ∠A1 en ∠C1 en ∠D1
c. ∠D3 = ∠B3 = 55º
d. ∠A2 = ∠B2 = 125º
e. ∠C4 = ∠B4 = 125º
80.
Tip:
Overstaande hoeken in een parallellogram zijn even groot.
a. ∠S4 = 180º - 52º = 128º (samen een gestrekte hoek)Overstaande hoeken in een parallellogram zijn even groot.
b. ∠P2 = ∠S2 = 128º
c. ∠Q1 = ∠S1 = ∠S3 = 52º
d. ∠S3 + ∠P2 + ∠Q1 + ∠R4 =
52º + 128º + 52º + 128º = 360º
81.
a. ∠K2 = ∠L2 (passen op elkaar)
∠L2 = 180º - 123º = 57º (samen een gestrekte hoek)
Dus: ∠K2 = 57º
b. ∠N4 = ∠L4 (passen op elkaar)
∠L4 = ∠L1 = 123º (overstaande hoeken)
Dus: ∠N4 = 123º
c. ∠M3 = ∠M2 (overstaande hoeken)
∠M2 = ∠L2 = (passen op elkaar)
Dus: ∠M3 = 57º
d. Samen zijn de hoeken van een vierhoek (en dus ook van een ruit) 360º.
82.
a. Teken een lijn door het midden van AB en het midden van CD. Dit is de symmetrieas. (zie afbeelding)
b. Ja, ∠A2 = ∠B1 (ivm symmetrieas / spiegelas)
c. ∠A2 past op ∠D2
d. ∠D4 past op ∠A4

83.
a.
∠A1 = 180º - 62º = 118º (samen een gestrekte hoek)
∠A2 = 62º (is gegeven)
∠A3 = ∠A2 = 62º (overstaande hoeken)
∠A4 = ∠A1 = 118º (overstaande hoeken)
Alle hoeken bij D zijn gelijk aan de hoeken bij A. Want deze passen op elkaar na verschuiven.
∠B1 = ∠A2 = 62º (symmetrieas)
∠B2 = 180º - 62º = 118º (samen een gestrekte hoek)
∠B3 = ∠B2 = 118º (overstaande hoeken)
∠B4 = ∠B1 = 62º (overstaande hoeken)
Alle hoeken bij C zijn gelijk aan de hoeken bij B. Want deze passen op elkaar na verschuiven.
b. Samen zijn de hoeken van een vierhoek (en dus ook van een trapezium) 360º.
84.
a. Ja, deze diagonaal is ook de symmetrieas van de vlieger.
b. ∠D past op ∠B
c. ∠A1 past op ∠A2
d. ∠C1 past op ∠C2
85.
Tip:
De som van de hoeken van een driehoek is 180 graden.
a. 180 gradenDe som van de hoeken van een driehoek is 180 graden.
b. 180 graden
c. 360 graden
86.
Tip:
∠P is een rechte hoek, dus 90º
∠Q = 360º - 90º - 100º - 85º∠P is een rechte hoek, dus 90º
∠Q = 85º
87.
b. De som van de hoeken in een vlieger is 360º, dus ∠K = 360º - 110º - 110º - 90º
Hieruit volgt dat ∠K = 50º.
88.
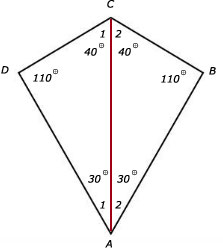
∠A1 = ∠A2 = 30º (ivm symmetrieas AC / diagonaal)
∠C1 = ∠C2 = 40º (ivm symmetrieas AC / diagonaal)
Voor de hoeken B en D blijft dan nog 220º over.
Dus ∠D = ∠B = 220º/2 = 110º
Tip:
In vlieger KLMN is KM de symmetrieas (spiegelas)
a. ∠L = ∠N = 110ºIn vlieger KLMN is KM de symmetrieas (spiegelas)
b. De som van de hoeken in een vlieger is 360º, dus ∠K = 360º - 110º - 110º - 90º
Hieruit volgt dat ∠K = 50º.
88.
∠A1 = ∠A2 = 30º (ivm symmetrieas AC / diagonaal)
∠C1 = ∠C2 = 40º (ivm symmetrieas AC / diagonaal)
Voor de hoeken B en D blijft dan nog 220º over.
Dus ∠D = ∠B = 220º/2 = 110º

Andere paragrafen:
1.1. Eigenschappen van vlakke figuren (1 t/m 14)
1.2. Namen van vlakke figuren (15 t/m 22)
1.3. Driehoeken (23 t/m 39)
1.4. Driehoeken tekenen (40 t/m 57)
1.5. Vierhoeken (58 t/m 76)
1.6. Hoeken berekenen in een vierhoek (77 t/m 88)
1.1. Eigenschappen van vlakke figuren (1 t/m 14)
1.2. Namen van vlakke figuren (15 t/m 22)
1.3. Driehoeken (23 t/m 39)
1.4. Driehoeken tekenen (40 t/m 57)
1.5. Vierhoeken (58 t/m 76)
1.6. Hoeken berekenen in een vierhoek (77 t/m 88)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


