TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 5.1 Kwadratische formules HAVO/VWO 2
Boek: Getal & Ruimte - Kwadraten en wortels HAVO/VWO 2 (deel 2) opgaven 1 t/m 11, 2013, 10e editie
1.
a. Bij x = 3 hoort y = 15
b. Bij x = 0 hoort y = -3
c. Bij x = -4 hoort y = 29
2.
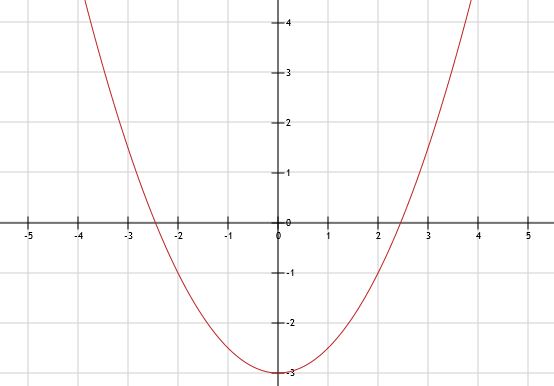
a. Het is een dalparabool. Er staat een positief getal voor de x2.
b. x = 3 invullen, levert y = 0,5 x (3)2 - 3 = 0,5 x 9 - 3 = 4,5 - 3 = 1,5
c. Zie afbeelding
3.
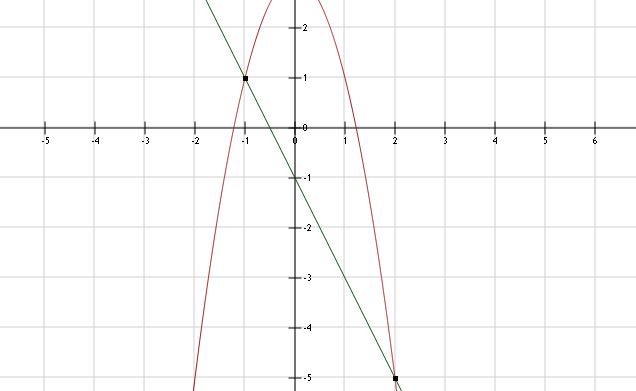
b. Zie afbeelding.
c. Coördinaten van de 2 snijpunten zijn: (-1,1) en (2,-5).
4.
Bij y = 0,5x2 hoort de rode grafiek.
Bij y = -x2 hoort de blauwe grafiek.
Bij y = -0,25x2 hoort de zwarte grafiek.
b. De dalparabolen zijn: II en IV
De bergparabolen zijn: I en III
5.
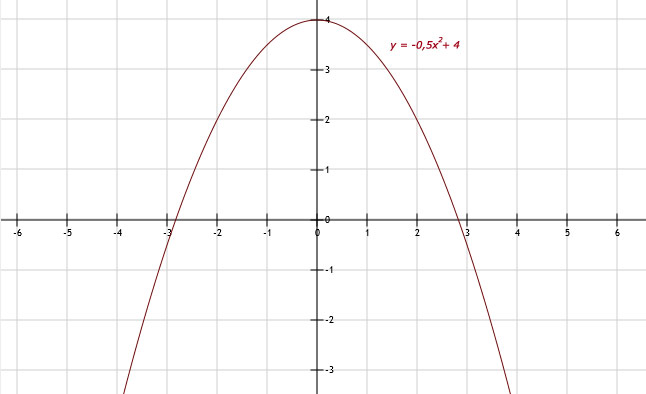
b. Het hoogste punt is de top. Dat is T(0,4).
c. Invullen x = 18 levert: -0,5 x (18)2 + 4 = -0,5 x 324 + 4 = -158
d. Invullen x = 26 levert: -0,5 x (26)2 + 4 = -0,5 x 676 + 4 = -334. Ja, punt ligt op de grafiek.
e. Invullen x = 6 levert: -0,5 x (6)2 + 4 = -0,5 x 36 + 4 = -14, dus dit punt ligt op de grafiek.
Invullen x = 16 levert: -0,5 x (16)2 + 4 = -0,5 x 256 + 4 = -124, dus dit punt ligt niet op de grafiek.
Invullen x = -5 levert: -0,5 x (-5)2 + 4 = -0,5 x 25 + 4 = -8,5, dus dit punt ligt op de grafiek.
Invullen x = -12 levert: -0,5 x (-12)2 + 4 = -0,5 x 144 + 4 = -68, dus dit punt ligt op de grafiek.
6.
b.
Invullen x = 7 levert: y = 0,25 x (7)2 - 1 = 11,25, dus dit punt ligt op de grafiek.
Invullen x = 10 levert: y = 0,25 x (10)2 - 1 = 24, dus dit punt ligt niet op de grafiek.
Invullen x = -8 levert: y = 0,25 x (-8)2 - 1 = 15, dus dit punt ligt op de grafiek.
7.
p = 0,25⋅(-4)2 - 1
p = 0,25⋅16 - 1
p = 4 - 1 = 3
p = 3
b. y = -3x2 + 8 door (5,q) levert:
q = -3⋅(5)2 + 8
q = -3⋅25 + 8
q = -67
c. y = ax2 door (2,8) levert:
8 = a⋅(2)2
8 = 4a
a = 2
d. y = -x2 + b door (-4,18) levert:
b = 34
8.
Het laagste punt is bij x = 0. Dit invullen levert: h = 0,03 x 02 = 0 meter.
Het hoogste punt is bij x = 4,5. Dit invullen levert: h = 0,03 x 4,52 = 0,6075 meter.
Dit levert een verschil in mm van: 607,5 mm.
b.
x = 2,25 invullen levert: h = 0,03 x 2,252 = 0,151875 meter.
Dit is dus ongeveer 15,2 cm.
Dus het midden ligt op een hoogte van 15,2 cm.
Dus de skeeler bevindt zich links van het midden.
9.
b.
Dat is bij x = 0. Dit is bij h = 25 meter.
c.
Het hoogste punt zit bij x = 120. Dit levert: h = 0,005 x 1202 + 25 = 97 (meter).
Het laagste punt zit bij x = 0. Dit levert: h = 0,005 x 02 + 25 = 25 (meter).
Het verschil is dus: 97 - 25 = 72 meter.
d.
x = 80 invullen, levert: h = 0,005 x 802 + 25 = 57 (meter).
Dus de lengte van AB is gelijk aan 57 meter.
10.
Bereken eerst x = 0. Dit levert: h = 0,00625 x 02 + 5 = 5 meter.
Dus de rode kabel hangt 5 + 4 = 9 meter boven het water.
b.
x = 40 invullen, levert: h = 0,00625 x 402 + 5 = 15 meter.
c.
De palen zitten bij x = -30, x = -20, x = -10, x = 0, x = 10, x = 20 en x = 30.
x = -30 invullen, levert: h = 0,00625 x (-30)2 + 5 = 10,625 meter.
x = -20 invullen, levert: h = 0,00625 x (-20)2 + 5 = 7,5 meter.
x = -10 invullen, levert: h = 0,00625 x (-10)2 + 5 = 5,625 meter.
x = 0 invullen, levert: h = 0,00625 x (0)2 + 5 = 5 meter.
x = 10 invullen, levert: h = 0,00625 x (10)2 + 5 = 5,625 meter.
x = 20 invullen, levert: h = 0,00625 x (20)2 + 5 = 7,5 meter.
x = 30 invullen, levert: h = 0,00625 x (30)2 + 5 = 10,625 meter.
Alles opgeteld, levert: 52,5 meter.
a. Bij x = 3 hoort y = 15
b. Bij x = 0 hoort y = -3
c. Bij x = -4 hoort y = 29
2.
a. Het is een dalparabool. Er staat een positief getal voor de x2.
b. x = 3 invullen, levert y = 0,5 x (3)2 - 3 = 0,5 x 9 - 3 = 4,5 - 3 = 1,5
c. Zie afbeelding

3.
Tip:
Als het getal voor de x2:
- positief is, dan is het een dalparabool
- negatief is, dan is het een bergparabool
a. y = -2x2 + 3 is een parabool. De andere formule is een rechte lijn.Als het getal voor de x2:
- positief is, dan is het een dalparabool
- negatief is, dan is het een bergparabool
b. Zie afbeelding.
c. Coördinaten van de 2 snijpunten zijn: (-1,1) en (2,-5).

4.
Tip:
Bij y = ax2 en a > 0 dan is het een dalparabool.
Bij y = ax2 en a < 0 dan is het een bergparabool.
a. Bij y = x2 hoort de groene grafiek.Bij y = ax2 en a > 0 dan is het een dalparabool.
Bij y = ax2 en a < 0 dan is het een bergparabool.
Bij y = 0,5x2 hoort de rode grafiek.
Bij y = -x2 hoort de blauwe grafiek.
Bij y = -0,25x2 hoort de zwarte grafiek.
b. De dalparabolen zijn: II en IV
De bergparabolen zijn: I en III
5.
Tip:
Om te bepalen of een punt P(x,y) op een parabool ligt, vul dit punt in en kijk of het klopt!
a.
Om te bepalen of een punt P(x,y) op een parabool ligt, vul dit punt in en kijk of het klopt!
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -0,5 | 2 | 3,5 | 4 | 3,5 | 2 | -0,5 |
b. Het hoogste punt is de top. Dat is T(0,4).
c. Invullen x = 18 levert: -0,5 x (18)2 + 4 = -0,5 x 324 + 4 = -158
d. Invullen x = 26 levert: -0,5 x (26)2 + 4 = -0,5 x 676 + 4 = -334. Ja, punt ligt op de grafiek.
e. Invullen x = 6 levert: -0,5 x (6)2 + 4 = -0,5 x 36 + 4 = -14, dus dit punt ligt op de grafiek.
Invullen x = 16 levert: -0,5 x (16)2 + 4 = -0,5 x 256 + 4 = -124, dus dit punt ligt niet op de grafiek.
Invullen x = -5 levert: -0,5 x (-5)2 + 4 = -0,5 x 25 + 4 = -8,5, dus dit punt ligt op de grafiek.
Invullen x = -12 levert: -0,5 x (-12)2 + 4 = -0,5 x 144 + 4 = -68, dus dit punt ligt op de grafiek.

6.
Tip:
Snijpunt y-as, dus x = 0, dus 0 invullen in de formule ofwel f(0).
a. Invullen x = 0 levert y = -1. Dus A(0,-1).Snijpunt y-as, dus x = 0, dus 0 invullen in de formule ofwel f(0).
b.
Invullen x = 7 levert: y = 0,25 x (7)2 - 1 = 11,25, dus dit punt ligt op de grafiek.
Invullen x = 10 levert: y = 0,25 x (10)2 - 1 = 24, dus dit punt ligt niet op de grafiek.
Invullen x = -8 levert: y = 0,25 x (-8)2 - 1 = 15, dus dit punt ligt op de grafiek.
7.
Tip:
Is het getal voor de x2 positief dan is het een dalparabool.
Is het getal voor de x2 negatief dan is het een bergparabool.
a. y = 0,25x2 - 1 door (-4,p) levert:Is het getal voor de x2 positief dan is het een dalparabool.
Is het getal voor de x2 negatief dan is het een bergparabool.
p = 0,25⋅(-4)2 - 1
p = 0,25⋅16 - 1
p = 4 - 1 = 3
p = 3
b. y = -3x2 + 8 door (5,q) levert:
q = -3⋅(5)2 + 8
q = -3⋅25 + 8
q = -67
c. y = ax2 door (2,8) levert:
8 = a⋅(2)2
8 = 4a
a = 2
d. y = -x2 + b door (-4,18) levert:
b = 34
8.
Tip:
Bij x = 0 is de hoogte gelijk aan 0.
a. Bij x = 0 is de hoogte gelijk aan 0.
Het laagste punt is bij x = 0. Dit invullen levert: h = 0,03 x 02 = 0 meter.
Het hoogste punt is bij x = 4,5. Dit invullen levert: h = 0,03 x 4,52 = 0,6075 meter.
Dit levert een verschil in mm van: 607,5 mm.
b.
x = 2,25 invullen levert: h = 0,03 x 2,252 = 0,151875 meter.
Dit is dus ongeveer 15,2 cm.
Dus het midden ligt op een hoogte van 15,2 cm.
Dus de skeeler bevindt zich links van het midden.
9.
Tip:
Het punt A ligt bij x = 80.
a.Het punt A ligt bij x = 80.
| x | 0 | 30 | 60 | 90 |
| h | 25 | 29,5 | 43 | 65,5 |
b.
Dat is bij x = 0. Dit is bij h = 25 meter.
c.
Het hoogste punt zit bij x = 120. Dit levert: h = 0,005 x 1202 + 25 = 97 (meter).
Het laagste punt zit bij x = 0. Dit levert: h = 0,005 x 02 + 25 = 25 (meter).
Het verschil is dus: 97 - 25 = 72 meter.
d.
x = 80 invullen, levert: h = 0,005 x 802 + 25 = 57 (meter).
Dus de lengte van AB is gelijk aan 57 meter.
10.
Tip:
AB = 80 meter, dan krijg je dus 2 stukken van 40 meter. Je vindt dit terug bij x = -40 en x = 40.
a.AB = 80 meter, dan krijg je dus 2 stukken van 40 meter. Je vindt dit terug bij x = -40 en x = 40.
Bereken eerst x = 0. Dit levert: h = 0,00625 x 02 + 5 = 5 meter.
Dus de rode kabel hangt 5 + 4 = 9 meter boven het water.
b.
x = 40 invullen, levert: h = 0,00625 x 402 + 5 = 15 meter.
c.
De palen zitten bij x = -30, x = -20, x = -10, x = 0, x = 10, x = 20 en x = 30.
x = -30 invullen, levert: h = 0,00625 x (-30)2 + 5 = 10,625 meter.
x = -20 invullen, levert: h = 0,00625 x (-20)2 + 5 = 7,5 meter.
x = -10 invullen, levert: h = 0,00625 x (-10)2 + 5 = 5,625 meter.
x = 0 invullen, levert: h = 0,00625 x (0)2 + 5 = 5 meter.
x = 10 invullen, levert: h = 0,00625 x (10)2 + 5 = 5,625 meter.
x = 20 invullen, levert: h = 0,00625 x (20)2 + 5 = 7,5 meter.
x = 30 invullen, levert: h = 0,00625 x (30)2 + 5 = 10,625 meter.
Alles opgeteld, levert: 52,5 meter.
11.
b. 45 : 2 = 22,5. Vul in x = 22,5 levert h(22,5) = 0,01 x 22,52 + 7 = 12,0625.
Dus de lampjes hangen op een hoogte van ca. 12 meter boven de x-as.
De weg zelf hangt 7 meter boven de x-as (bereken hiertoe x = 0). Dus de lampjes hangen 12,0625 - 7 = 5,0625 meter boven de weg.
c. Vul in x = 25 levert h(25) = 0,01 x 252 + 7 = 13,25. Dus minder dan 50 meter uit elkaar.
Tip:
x is de afstand die je loopt vanaf de verticale lijn h naar links of rechts.
a. Vul in x = 50 levert h(50) = 0,01 x 502 + 7 = 32. Dus de pylonen zijn 32 meter hoog.x is de afstand die je loopt vanaf de verticale lijn h naar links of rechts.
b. 45 : 2 = 22,5. Vul in x = 22,5 levert h(22,5) = 0,01 x 22,52 + 7 = 12,0625.
Dus de lampjes hangen op een hoogte van ca. 12 meter boven de x-as.
De weg zelf hangt 7 meter boven de x-as (bereken hiertoe x = 0). Dus de lampjes hangen 12,0625 - 7 = 5,0625 meter boven de weg.
c. Vul in x = 25 levert h(25) = 0,01 x 252 + 7 = 13,25. Dus minder dan 50 meter uit elkaar.
Andere paragrafen:
5.1. Kwadratische formules (1 t/m 11)
5.2. Wortelformules (12 t/m 20)
5.3. Rekenen met wortels (21 t/m 46)
5.4. De vergelijking x2 = c (47 t/m 59)
5.5. Soorten getallen (60 t/m 73)
5.1. Kwadratische formules (1 t/m 11)
5.2. Wortelformules (12 t/m 20)
5.3. Rekenen met wortels (21 t/m 46)
5.4. De vergelijking x2 = c (47 t/m 59)
5.5. Soorten getallen (60 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


