TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 5.3 Rekenen met wortels HAVO/VWO 2
Boek: Getal & Ruimte - Kwadraten en wortels HAVO/VWO 2 (deel 2) opgaven 21 t/m 46, 2013, 10e editie
21.
b. (√15)2 = 15
22.
a. Op basis van afrondingsverschillen krijg je inderdaad 5,0176.
(√5)2 = 5
b. (√8)2 = 8
(√79)2 = 79
(√19 500)2 = 19 500
(√a)2 = a
23.
9⋅6 = 54
b.
4⋅7 = 28
c.
5⋅3 = 15
d.
-8⋅2 = -16
e.
11 - 9 = 2
f.
9 - 3⋅6 = 9 - 18 = -9
24.
b. 3 ⋅ 3 + 7 ⋅ 5 = 9 + 35 = 44
c. 5 - 25 = -20
d. 25 ⋅ 2 - 3 ⋅ 6 = 50 - 18 = 32
e. -5 ⋅ 9 - 18 = -45 - 18 = -63
f. 18 - 6 = 12
25.
√8 ≈ 2,828
Karin heeft dus geen gelijk.
b. Op rekenmachine: √5 x √3 ≈ 3,873
√15 ≈ 3,873
Chris heeft dus wel gelijk.
c. Theo heeft gelijk.
26.
a. 8√2
b. 6√3
c. 4√7
27.
b. 11√2
c. kan niet korter
d. kan niet korter
e. 4√6
f. 2 x 2 + 3 = 7
28.
b. 10 ⋅ √9 = 30
c. 3 ⋅ √81 = 27
d. 2 - 5 = -3
e. 15 ⋅ √64 = 15 ⋅ 8 = 120
f. 48
29.
b. 50 - 12 = 38
c. 15√16 = 15 ⋅ 4 = 60
d. 36√5
e. -√2
f. kan niet korter
30.
v = 3,5 ⋅ √5 ⋅ √r
3,5 x √5 ≈ 7,83
v = 7,83⋅√r
Tip:
(√a)2 = a
a. (√10)2 = 10(√a)2 = a
b. (√15)2 = 15
22.
a. Op basis van afrondingsverschillen krijg je inderdaad 5,0176.
(√5)2 = 5
b. (√8)2 = 8
(√79)2 = 79
(√19 500)2 = 19 500
(√a)2 = a
23.
Tip:
Bij c: let op: de 5 staat voor het kwadraat!
a. Bij c: let op: de 5 staat voor het kwadraat!
9⋅6 = 54
b.
4⋅7 = 28
c.
5⋅3 = 15
d.
-8⋅2 = -16
e.
11 - 9 = 2
f.
9 - 3⋅6 = 9 - 18 = -9
24.
Tip:
(-√5)2 = (-1)2 ⋅ (√5)2 = 1 ⋅ 5 = 5
a. 9 ⋅ 2 - 4 ⋅ 5 = 18 - 20 = -2(-√5)2 = (-1)2 ⋅ (√5)2 = 1 ⋅ 5 = 5
b. 3 ⋅ 3 + 7 ⋅ 5 = 9 + 35 = 44
c. 5 - 25 = -20
d. 25 ⋅ 2 - 3 ⋅ 6 = 50 - 18 = 32
e. -5 ⋅ 9 - 18 = -45 - 18 = -63
f. 18 - 6 = 12
25.
Tip:
√a + √b ≠ √(a+b)
Dus √4 + √9 ≠ √13, want er zou 5 moeten uitkomen (2 + 3).
√a x √b = √(ab)
Dus √4 x √9 = √36, en inderdaad 2 x 3 = 6
Wortels zomaar optellen mag dus niet, wortels vermenigvuldigen wel.
a. Op rekenmachine: √5 + √3 ≈ 3,968√a + √b ≠ √(a+b)
Dus √4 + √9 ≠ √13, want er zou 5 moeten uitkomen (2 + 3).
√a x √b = √(ab)
Dus √4 x √9 = √36, en inderdaad 2 x 3 = 6
Wortels zomaar optellen mag dus niet, wortels vermenigvuldigen wel.
√8 ≈ 2,828
Karin heeft dus geen gelijk.
b. Op rekenmachine: √5 x √3 ≈ 3,873
√15 ≈ 3,873
Chris heeft dus wel gelijk.
c. Theo heeft gelijk.
26.
a. 8√2
b. 6√3
c. 4√7
27.
Tip:
Gelijksoortige wortels kun je optellen: dus 3√4 + 4√4 = 7√4
En dat klopt want er moet in beide gevallen 14 uitkomen.
a. 9√7Gelijksoortige wortels kun je optellen: dus 3√4 + 4√4 = 7√4
En dat klopt want er moet in beide gevallen 14 uitkomen.
b. 11√2
c. kan niet korter
d. kan niet korter
e. 4√6
f. 2 x 2 + 3 = 7
28.
Tip:
a√b ⋅ c√d = ac√bd
Voorbeeld: 2√3 ⋅ 4√5 = 8√15
a. 10 ⋅ √18 = 10√18a√b ⋅ c√d = ac√bd
Voorbeeld: 2√3 ⋅ 4√5 = 8√15
b. 10 ⋅ √9 = 30
c. 3 ⋅ √81 = 27
d. 2 - 5 = -3
e. 15 ⋅ √64 = 15 ⋅ 8 = 120
f. 48
29.
Tip:
Er kan wel een min "voor" de wortel staan, maar nooit "onder" de wortel.
Dus -√2 kan wel, maar √-2 kan niet!
a. 21√10Er kan wel een min "voor" de wortel staan, maar nooit "onder" de wortel.
Dus -√2 kan wel, maar √-2 kan niet!
b. 50 - 12 = 38
c. 15√16 = 15 ⋅ 4 = 60
d. 36√5
e. -√2
f. kan niet korter
30.
Tip:
√a ⋅ √b = √(ab)
v = 3,5⋅√(5r)√a ⋅ √b = √(ab)
v = 3,5 ⋅ √5 ⋅ √r
3,5 x √5 ≈ 7,83
v = 7,83⋅√r
31.
= 5√3 + 2√3 + 5√3 + 2√3
= 14√3 cm
≈ 24,2 cm
Oppervlakte PQRS = lengte x breedte
= PQ x QR
= 5√3 x 2√3
= 10⋅√3⋅√3
= 10⋅3
= 30 cm2
32.
a. (5√2)2 = 25 ⋅ 2 = 50 en (√50)2 = 50
b. Ja, die zijn gelijk aan elkaar.
c. (2√6)2 = 4 ⋅ 6 = 24 en (√24)2 = 24
d. Ja, die zijn gelijk aan elkaar.
33.
b. √12 = √4 ⋅ √3 = 2√3
c. √50 = √25 ⋅ √2 = 5√2
d. √63 = √9 ⋅ √7 = 3√7
e. √27 = √9 ⋅ √3 = 3√3
f. √45 = √9 ⋅ √5 = 3√5
34.
b. √288 = √144 ⋅ √2 = 12√2
c. √108 = √36 ⋅ √3 = 6√3
d. √200 = √100 ⋅ √2 = 10√2
e. √216 = √36 ⋅ √6 = 6√6
f. √800 = √400 ⋅ √2 = 20√2
35.
a. Werk met √6 levert: 3√6 + 2√6 = 5√6
b. Werk met √2 levert: 5√2 + 4√2 = 9√2
c. Werk met √2 levert: 2√2 + 3√2 = 5√2
d. Werk met √3 levert: √3 + 2√3 + 3√3 = 6√3
e. Werk met √5 levert: 3 ⋅ √4 ⋅ √5 - √9 ⋅ √5 =6√5 - 3√5 = 3√5
f. Werk met √6 levert: 2√6 - 8√6 + 6√6 = 0
36.
PR2 + (3√2)2 = (5√2)2
PR2 + 9⋅2 = 25⋅2
PR2 + 18 = 50
PR2 = 32
PR = √32
Omtrek driehoek PQR = PR + QR + PQ
= √32 + 3√2 + 5√2
= √16⋅√2 + 3√2 + 5√2
= 4√2 + 3√2 + 5√2
= 12√2 cm
Opp. driehoek PQR = 1/2 x zijde x hoogte
= 1/2 x QR x PR
= 1/2 ⋅ 3√2 ⋅ √32
= 1,5 ⋅ √64
= 1,5 ⋅ 8
= 12 cm2
37.
DE2 + (√5)2 = (5√2)2
DE2 + 5 = 50
DE2 = 45
DE = √45
Omtrek DEFG = DE + EF + GF + DG
= √45 + √5 + √45 + √5
= 2√45 + 2√5
= 2⋅√9⋅√5 + 2√5
= 2⋅3⋅√5 + 2√5
= 6√5 + 2√5
= 8√5 cm
Oppervlakte DEFG = lengte x breedte
= DE x EF
= √45 x √5
= √225
= 15 cm2
38.
AC2 = AD2 + CD2
AC2 = (2√3)2 + 42
AC2 = 4⋅3 + 16
AC2 = 12 + 16
AC2 = 28
AC = √28 = √4 ⋅ √7 = 2√7
BC2 = BD2 + CD2
82 = BD2 + 42
64 = BD2 + 16
BD2 = 48
BD = √48 = √16 ⋅ √3 = 4√3
Omtrek = AD + BD + BC + AC
= 2√3 + 4√3 + 8 + 2√7
= 6√3 + 8 + 2√7 cm
b.
Oppervlakte = 1/2 x zijde x hoogte
= 1/2 x AB x CD
= 1/2 x (2√3 + 4√3) x 4
= 1/2 x 6√3 x 4
= 12√3 cm2
c.
De vraag is of dat geldt:
AC2 + BC2 = AB2 (?)
28 + 82 = (6√3)2 (?)
28 + 64 = 36⋅3 (?)
92 = 108 (?)
Neen, dit klopt niet. Dus de driehoek ABC is niet rechthoekig.
39.
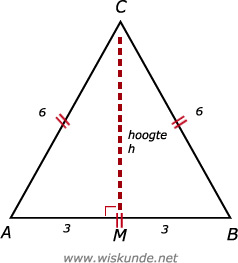
32 + h2 = 62
h2 = 36 - 9
h2 = 27
h = √27 = √9 ⋅ √3 = 3√3
Oppervlakte driehoek ABC = 1/2 x zijde x hoogte
= 1/2 x AB x CM (bedenk dat CM is gelijk aan h)
= 1/2 x 6 x 3√3
= 9√3 cm2
40.
AB2 + BC2 = AC2
82 + 82 = AC2
AC2 = 64 + 64
AC2 = 128
AC = √128 = √64 ⋅ √2 = 8√2
AS = ½AC = 1/2 x 8√2 = 4√2 cm.
b.
Bedenk dat: BD = AC
Omtrek driehoek BDT = BD + BT + DT
= 8√2 + 8 + 8
= 16 + 8√2 cm
c.
Bereken eerst ST.
DS2 + ST2 = DT2
(4√2)2 + ST2 = 82
16⋅2 + ST2 = 64
ST2 = 64-32
ST2 = 32
ST = √32 = √16 ⋅ √2 = 4√2
Oppervlakte (driehoek)BDT = 1/2 x zijde x hoogte
= 1/2 x BD x ST
= 1/2 x 8√2 x 4√2
= 4√2 x 4√2
= 16 x 2
= 32 cm2

Tip:
omtrek rechthoek => tel alle zijden op
opp. rechthoek = lengte x breedte
Omtrek PQRS = PQ + QR + RS + PSomtrek rechthoek => tel alle zijden op
opp. rechthoek = lengte x breedte
= 5√3 + 2√3 + 5√3 + 2√3
= 14√3 cm
≈ 24,2 cm
Oppervlakte PQRS = lengte x breedte
= PQ x QR
= 5√3 x 2√3
= 10⋅√3⋅√3
= 10⋅3
= 30 cm2
32.
a. (5√2)2 = 25 ⋅ 2 = 50 en (√50)2 = 50
b. Ja, die zijn gelijk aan elkaar.
c. (2√6)2 = 4 ⋅ 6 = 24 en (√24)2 = 24
d. Ja, die zijn gelijk aan elkaar.
33.
Tip:
Ken je kwadraten om een factor voor het wortelteken te brengen. Breng het grootst mogelijke kwadraat voor de wortel.
Bijvoorbeeld: √100 = √25 ⋅ √4 = 5√4 = 5 ⋅ 2 = 10
a. √28 = √4 ⋅ √7 = 2√7Ken je kwadraten om een factor voor het wortelteken te brengen. Breng het grootst mogelijke kwadraat voor de wortel.
Bijvoorbeeld: √100 = √25 ⋅ √4 = 5√4 = 5 ⋅ 2 = 10
b. √12 = √4 ⋅ √3 = 2√3
c. √50 = √25 ⋅ √2 = 5√2
d. √63 = √9 ⋅ √7 = 3√7
e. √27 = √9 ⋅ √3 = 3√3
f. √45 = √9 ⋅ √5 = 3√5
34.
Tip:
Om √200 te herleiden, gaan we kijken door welk grootste kwadraat we deze kunnen delen. Het heeft geen zin om kwadraten te proberen die groter zijn dan de helft van √200.
a. √120 = √4 ⋅ √30 = 2√30Om √200 te herleiden, gaan we kijken door welk grootste kwadraat we deze kunnen delen. Het heeft geen zin om kwadraten te proberen die groter zijn dan de helft van √200.
b. √288 = √144 ⋅ √2 = 12√2
c. √108 = √36 ⋅ √3 = 6√3
d. √200 = √100 ⋅ √2 = 10√2
e. √216 = √36 ⋅ √6 = 6√6
f. √800 = √400 ⋅ √2 = 20√2
35.
a. Werk met √6 levert: 3√6 + 2√6 = 5√6
b. Werk met √2 levert: 5√2 + 4√2 = 9√2
c. Werk met √2 levert: 2√2 + 3√2 = 5√2
d. Werk met √3 levert: √3 + 2√3 + 3√3 = 6√3
e. Werk met √5 levert: 3 ⋅ √4 ⋅ √5 - √9 ⋅ √5 =6√5 - 3√5 = 3√5
f. Werk met √6 levert: 2√6 - 8√6 + 6√6 = 0
36.
Tip:
Omtrek driehoek PQR = PR + QR + PQ
Opp. driehoek PQR = 1/2 x zijde x hoogte
Bereken eerst PR met de Stelling van Pythagoras!
PR2 + QR2 = PQ2Omtrek driehoek PQR = PR + QR + PQ
Opp. driehoek PQR = 1/2 x zijde x hoogte
Bereken eerst PR met de Stelling van Pythagoras!
PR2 + (3√2)2 = (5√2)2
PR2 + 9⋅2 = 25⋅2
PR2 + 18 = 50
PR2 = 32
PR = √32
Omtrek driehoek PQR = PR + QR + PQ
= √32 + 3√2 + 5√2
= √16⋅√2 + 3√2 + 5√2
= 4√2 + 3√2 + 5√2
= 12√2 cm
Opp. driehoek PQR = 1/2 x zijde x hoogte
= 1/2 x QR x PR
= 1/2 ⋅ 3√2 ⋅ √32
= 1,5 ⋅ √64
= 1,5 ⋅ 8
= 12 cm2
37.
Tip:
Bereken eerst DE met de Stelling van Pythagoras.
DE2 + EF2 = DF2Bereken eerst DE met de Stelling van Pythagoras.
DE2 + (√5)2 = (5√2)2
DE2 + 5 = 50
DE2 = 45
DE = √45
Omtrek DEFG = DE + EF + GF + DG
= √45 + √5 + √45 + √5
= 2√45 + 2√5
= 2⋅√9⋅√5 + 2√5
= 2⋅3⋅√5 + 2√5
= 6√5 + 2√5
= 8√5 cm
Oppervlakte DEFG = lengte x breedte
= DE x EF
= √45 x √5
= √225
= 15 cm2
38.
Tip:
Bij c: Gebruik de omgekeerde Stelling van Pythagoras.
a.Bij c: Gebruik de omgekeerde Stelling van Pythagoras.
AC2 = AD2 + CD2
AC2 = (2√3)2 + 42
AC2 = 4⋅3 + 16
AC2 = 12 + 16
AC2 = 28
AC = √28 = √4 ⋅ √7 = 2√7
BC2 = BD2 + CD2
82 = BD2 + 42
64 = BD2 + 16
BD2 = 48
BD = √48 = √16 ⋅ √3 = 4√3
Omtrek = AD + BD + BC + AC
= 2√3 + 4√3 + 8 + 2√7
= 6√3 + 8 + 2√7 cm
b.
Oppervlakte = 1/2 x zijde x hoogte
= 1/2 x AB x CD
= 1/2 x (2√3 + 4√3) x 4
= 1/2 x 6√3 x 4
= 12√3 cm2
c.
De vraag is of dat geldt:
AC2 + BC2 = AB2 (?)
28 + 82 = (6√3)2 (?)
28 + 64 = 36⋅3 (?)
92 = 108 (?)
Neen, dit klopt niet. Dus de driehoek ABC is niet rechthoekig.
39.
Tip:
Maak eerst een schets. Bereken dan de hoogte h. Ofwel CM.
Bedenk bij een gelijkzijdige driehoek: AB = BC = AC
AM2 + CM2 = AC2Maak eerst een schets. Bereken dan de hoogte h. Ofwel CM.
Bedenk bij een gelijkzijdige driehoek: AB = BC = AC
32 + h2 = 62
h2 = 36 - 9
h2 = 27
h = √27 = √9 ⋅ √3 = 3√3
Oppervlakte driehoek ABC = 1/2 x zijde x hoogte
= 1/2 x AB x CM (bedenk dat CM is gelijk aan h)
= 1/2 x 6 x 3√3
= 9√3 cm2

40.
Tip:
Bereken AC met de Stelling van Pythagoras.
AS = ½AC
∠ABC = 90º
a.Bereken AC met de Stelling van Pythagoras.
AS = ½AC
∠ABC = 90º
AB2 + BC2 = AC2
82 + 82 = AC2
AC2 = 64 + 64
AC2 = 128
AC = √128 = √64 ⋅ √2 = 8√2
AS = ½AC = 1/2 x 8√2 = 4√2 cm.
b.
Bedenk dat: BD = AC
Omtrek driehoek BDT = BD + BT + DT
= 8√2 + 8 + 8
= 16 + 8√2 cm
c.
Bereken eerst ST.
DS2 + ST2 = DT2
(4√2)2 + ST2 = 82
16⋅2 + ST2 = 64
ST2 = 64-32
ST2 = 32
ST = √32 = √16 ⋅ √2 = 4√2
Oppervlakte (driehoek)BDT = 1/2 x zijde x hoogte
= 1/2 x BD x ST
= 1/2 x 8√2 x 4√2
= 4√2 x 4√2
= 16 x 2
= 32 cm2

41.
b. √6/√2 = √3, want √3 ⋅ √2 = √6
42.
b. 2√6
c. 4√3
d. 3√1 = 3
e. 2√7
f. 2,5√5
g. 1 ⋅ √6 = √6
h. 1/2
43.
b. 4√20 = 4 ⋅ √4 ⋅ √5 = 4 ⋅ 2 ⋅ √5 = 8√5
c. 2,5√8 = 2,5 ⋅ √4 ⋅ √2 = 2,5 ⋅ 2 ⋅ √2 = 5√2
d. 3√4 = 3 ⋅ 2 = 6
44.
b. 2/7√7
c. 2⋅√50 = 2⋅√25⋅√2 = 2⋅5⋅√2 = 10√2
d. 1,5⋅√60 = 1,5⋅√4⋅√15 = 1,5⋅2⋅√15 = 3√15
e. √(21/4) = √21 / √4 = √21 / 2 = ½√21
f. √(81/16) = √81 / √16 = 9/4 = 2 1/4
g. √(5/4) = √5 / √4 = (√5) / 2 = ½√5
h. √(28/9) = √28 / √9 = (√4⋅√7) / 3 = (2√7) / 3 = 2/3√7
45.
a. √(10/9) = √10 / √9 = √10 / 3 = 1/3√10
b. √(20/9) = √20 / √9 = (√4⋅√5) / √9 = (2√5) / 3 = 2/3√5
c. √(78/25) = √78 / √25 = √78 / 5 = 1/5√78
d. √(169/64) = √169 / √64 = 13/8 = 1 5/8
46.
*
Tip:
√a / √b = √(a/b)
a. 6/2 = 3, want 3 ⋅ 2 = 6√a / √b = √(a/b)
b. √6/√2 = √3, want √3 ⋅ √2 = √6
42.
Tip:
√a / √b = √(a/b)
a. 2√2√a / √b = √(a/b)
b. 2√6
c. 4√3
d. 3√1 = 3
e. 2√7
f. 2,5√5
g. 1 ⋅ √6 = √6
h. 1/2
43.
Tip:
√a / √b = √(a/b)
√a x √b = √(ab)
a. 4√4 = 4 ⋅ 2 = 8√a / √b = √(a/b)
√a x √b = √(ab)
b. 4√20 = 4 ⋅ √4 ⋅ √5 = 4 ⋅ 2 ⋅ √5 = 8√5
c. 2,5√8 = 2,5 ⋅ √4 ⋅ √2 = 2,5 ⋅ 2 ⋅ √2 = 5√2
d. 3√4 = 3 ⋅ 2 = 6
44.
Tip:
√a / √b = √(a/b)
√a x √b = √(ab)
a. 1/6√5√a / √b = √(a/b)
√a x √b = √(ab)
b. 2/7√7
c. 2⋅√50 = 2⋅√25⋅√2 = 2⋅5⋅√2 = 10√2
d. 1,5⋅√60 = 1,5⋅√4⋅√15 = 1,5⋅2⋅√15 = 3√15
e. √(21/4) = √21 / √4 = √21 / 2 = ½√21
f. √(81/16) = √81 / √16 = 9/4 = 2 1/4
g. √(5/4) = √5 / √4 = (√5) / 2 = ½√5
h. √(28/9) = √28 / √9 = (√4⋅√7) / 3 = (2√7) / 3 = 2/3√7
45.
a. √(10/9) = √10 / √9 = √10 / 3 = 1/3√10
b. √(20/9) = √20 / √9 = (√4⋅√5) / √9 = (2√5) / 3 = 2/3√5
c. √(78/25) = √78 / √25 = √78 / 5 = 1/5√78
d. √(169/64) = √169 / √64 = 13/8 = 1 5/8
46.
*
Andere paragrafen:
5.1. Kwadratische formules (1 t/m 11)
5.2. Wortelformules (12 t/m 20)
5.3. Rekenen met wortels (21 t/m 46)
5.4. De vergelijking x2 = c (47 t/m 59)
5.5. Soorten getallen (60 t/m 73)
5.1. Kwadratische formules (1 t/m 11)
5.2. Wortelformules (12 t/m 20)
5.3. Rekenen met wortels (21 t/m 46)
5.4. De vergelijking x2 = c (47 t/m 59)
5.5. Soorten getallen (60 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


