Uitwerking 6.4 Pythagoras in de ruimte opgave 49
01-07-2025
admin
Getal & Ruimte HAVO/VWO 2 (deel 2) hoofdstuk 6 De stelling van Pythagoras
Uitleg
Schets vierkant ABCD en teken en bereken BD. Met de zojuist berekende BD en HD = 4 kun je BH berekenen. Hetzelfde doe je bij HJ.
Om te kijken of hoek H recht is, bepaal of BH2 + HJ2 gelijk is aan BJ2. Zoja, dan is de hoek H recht.
Vraag 49
Gegeven 2 kubussen met ribben 4 cm boven op elkaar. Bereken BH en HJ. Is driehoek BHJ rechthoekig?
Antwoord
a.
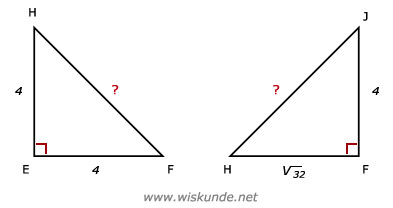
Bereken eerst FH in driehoek EFH.
EF(kwadraat) + EH(kwadraat) = FH(kwadraat)
4(kwadraat) + 4(kwadraat) = FH(kwadraat)
FH(kwadraat) = 32
FH = (wortel)32
FH (ongeveer) 5,66 cm
FH(kwadraat) + FJ(kwadraat) = HJ(kwadraat)
32 + 4(kwadraat) = HJ(kwadraat)
HJ(kwadraat) = 48
HJ = (wortel)48
HJ (ongeveer) 6,93 cm
Dus BH = HJ = (wortel)48 (ongeveer) 6,93 cm.
b.
Als (hoek)BHJ rechthoekig is, dan moet gelden:
BH(kwadraat) + HJ(kwadraat) = BJ(kwadraat) (is dat wel zo?)
48 + 48 =(?) 8(kwadraat)
96 =(?) 64
Nee, je ziet dat de Stelling van Pythagoras niet geldt. Dus (hoek)BHJ is niet rechthoekig.
Uitwerking
Wil je meer uitleg over: Reageer op deze uitwerking
Heb je een vraag over deze opgave, snap je iets niet of ben je een fout tegengekomen en wil je binnen 10 minuten antwoord? Stel een vraag!