Uitwerking 6.4 Pythagoras in de ruimte opgave 50
01-07-2025
admin
Getal & Ruimte HAVO/VWO 2 (deel 2) hoofdstuk 6 De stelling van Pythagoras
Uitleg
Bereken AP2 + BP2. En bereken AB2. Als geldt dat AP2 + BP2 = AB2 dan is de hoek recht. Bereken m.b.v. EP en AE de lengte van AP.
Vraag 50
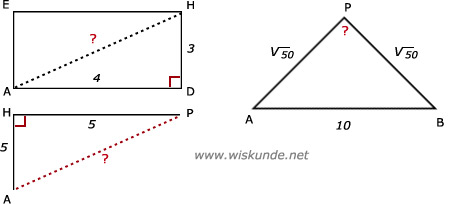
Gegeven een balk met afmetingen 10, 4 en 3 cm. P ligt in het midden van GH. Onderzoek of de hoek ABP een rechte hoek is.
Antwoord
Bereken eerst AH in driehoek ADH.
AD(kwadraat) + DH(kwadraat) = AH(kwadraat)
4(kwadraat) + 3(kwadraat) = AH(kwadraat)
AH(kwadraat) = 25
AH = (wortel)25
AH = 5
Bereken dan AP in driehoek AHP.
AH(kwadraat) + HP(kwadraat) = AP(kwadraat)
5(kwadraat) + 5(kwadraat) = AP(kwadraat)
AP(kwadraat) = 50
AP = (wortel)50
AP (ongeveer) 7,07
We hebben nu een "mogelijke" Pythagoras driehoek ABP.
Dan moet dus gelden:
AP(kwadraat) + BP(kwadraat) = AB(kwadraat) (Is dat wel zo?)
((wortel)50)(kwadraat) + ((wortel)50)(kwadraat) = 10(kwadraat) (?)
50 + 50 = 100 (?)
100 = 100
Ja, dat klopt zeker! Dus dan moet de hoek wel 90(graden) zijn.
Dus driehoek ABP is rechthoekig.
Uitwerking
Wil je meer uitleg over: Reageer op deze uitwerking
Heb je een vraag over deze opgave, snap je iets niet of ben je een fout tegengekomen en wil je binnen 10 minuten antwoord? Stel een vraag!