TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.3 Kwadratische functies HAVO 3
Boek: Getal & Ruimte - Kwadratische problemen HAVO 3 (deel 1) opgaven 24 t/m 35, 2010De basisformulering van een formule is van de vorm: y = ax + b. We kunnen ook de haakjesnotatie gebruiken: f(x) = ax + b.
Dus bij de formule y = 4x - 5 hoort de functie f(x) = 4x - 5. Het is een andere manier van noteren, maar het gaat over hetzelfde.
Een functie moet je zien als een soort machientje. Je stopt er iets in, en er komt iets uit. Wat je er in stopt, is 'x' en wat er uitkomt, is 'y'.
Zo levert f(3) als uitkomst 7. We noemen 3 dan het origineel en 7 het beeld (of functiewaarde).
Dus bij de formule y = 4x - 5 hoort de functie f(x) = 4x - 5. Het is een andere manier van noteren, maar het gaat over hetzelfde.
Een functie moet je zien als een soort machientje. Je stopt er iets in, en er komt iets uit. Wat je er in stopt, is 'x' en wat er uitkomt, is 'y'.
Zo levert f(3) als uitkomst 7. We noemen 3 dan het origineel en 7 het beeld (of functiewaarde).
24.
f(4) = (4)2 + 3 = 16 + 3 = 19
f(-4) = (-4)2 + 3 = 16 + 3 = 19
f(0) = (0)2 + 3 = 0 + 3 = 3
b.
De haakjesnotatie van f is f(x) = x2 + 3.
25.
y = x2 - 4
b.
f(5) = (5)2 - 4 = 25 - 4 = 21
f(-2) = (-2)2 - 4 = 4 - 4 = 0
c.
f(3) = (3)2 - 4 = 9 - 4 = 5
A(3,5) ligt op de grafiek omdat 5 het beeld is van origineel 3.
d.
f(6) = (6)2 - 4 = 36 - 4 = 32
Dus punt (6,32) ligt op de grafiek van f.
26.
g(5) = -3 ⋅ (5)2 + 7 = -3 ⋅ 25 + 7 = -75 + 7 = -68
g(-1) = -3 ⋅ (-1)2 + 7 = -3 ⋅ 1 + 7 = -3 + 7 = 4
b.
g(0) = -3 ⋅ (0)2 + 7 = -3 ⋅ 0 + 7 = 0 + 7 = 7
Dus het punt (0,7) ligt op de grafiek van g.
c.
g(-2) = -3 ⋅ (-2)2 + 7 = -3 ⋅ 4 + 7 = -12 + 7 = -5
Dus het punt (-2,-5) ligt op de grafiek van g.
27.
g(5) = -2 ⋅ (5)2 + 8 ⋅ 5 = -2 ⋅ 25 + 40 = -50 + 40 = -10
g(-3) = -2 ⋅ (-3)2 + 8 ⋅ -3 = -2 ⋅ 9 - 24 = -18 - 24 = -42
b.
y = -2x2 + 8x
c.
g(-1) = -2 ⋅ (-1)2 + 8 ⋅ -1 = -2 ⋅ 1 - 8 = -2 - 8 = -10
Dus het punt P(-1,-10) ligt op de grafiek.
28.
h(5) = (5)2 - 7 ⋅ 5 - 5 = 25 - 35 - 5 = -15
h(-4) = (-4)2 - 7 ⋅ -4 - 5 = 16 + 28 - 5 = 39
b.
A(-1,y), dus YA => h(-1) = (-1)2 - 7 ⋅ -1 - 5 = 1 + 7 - 5 = 3
Dus we hebben dan het punt A(-1,3).
c.
B(6,y), dus YB => h(6) = (6)2 - 7 ⋅ 6 - 5 = 36 - 42 - 5 = -11
Dus we hebben dan het punt B(6,-11).
29.
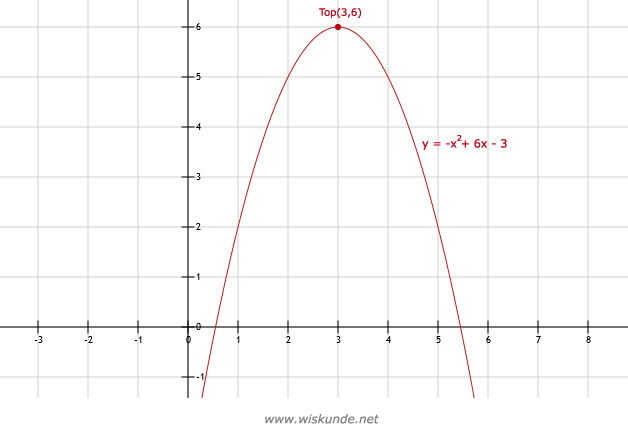
a = -1, b = 6, c = -3
Xtop = -b/2a = -6/-2 = 3
Ytop = f(3) = -(3)2 + 6 ⋅ 3 - 3
= -9 + 18 - 3
= 6
Dus de top is: Top(3,6).
b.
30.
a = 0,5, b = 2, c = 1
Xtop = -b/2a = -2/1 = -2
Ytop = g(-2) = 0,5 ⋅ (-2)2 + 2 ⋅ -2 + 1 = 0,5 ⋅ 4 - 4 + 1 = 2 - 4 + 1 = -1
Dus de top is: Top(-2,-1).
b.
g(10) = 0,5 ⋅ (10)2 + 2 ⋅ 10 + 1 = 0,5 ⋅ 100 + 20 + 1 = 50 + 20 + 1 = 71
Dus (10,71) ligt op de grafiek, en dus niet (10,31).
31.
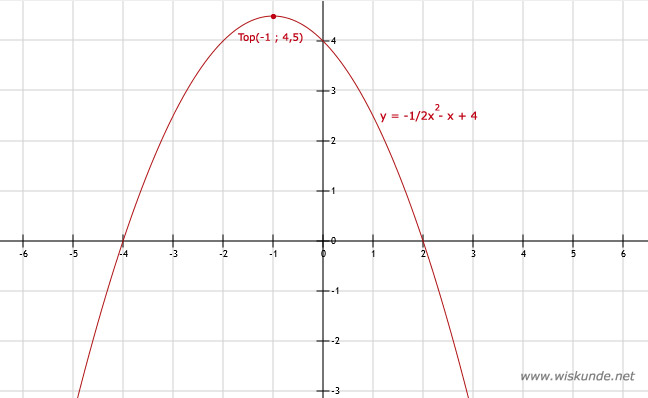
a = -0,5, b = -1, c = 4
Xtop = -b/2a = 1/-1 = -1
Ytop = h(-1) = -0,5 ⋅ (-1)2 - -1 + 4 = -0,5 ⋅ 1 + 1 + 4 = 4½
Dus de top is: Top(-1,4½).
b.
c.
h(-10) = -0,5 ⋅ (-10)2 - -10 + 4 = -0,5 ⋅ 100 + 10 + 4 = -50 + 14 = -36
Dus P(-10,-36) ligt op de grafiek van h.
32.
a = -0,24, b = 2,4, c = 2
Xtop = -b/2a = -2,4/-0,48 = 5
Ytop = f(5) = -0,24 ⋅ (5)2 + 2,4 ⋅ 5 + 2 = -0,24 ⋅ 25 + 12 + 2 = -6 + 14 = 8
Dus de top is: Top(5,8).
b.
Bereken f(0) levert:
f(0) = -0,24 ⋅ (0)2 + 2,4 ⋅ 0 + 2 = 0 + 0 + 2 = 2
Dus hij laat de bal los op een hoogte van 2 meter.
c.
Bereken f(9,9) levert:
f(9,9) = -0,24 ⋅ (9,9)2 + 2,4 ⋅ 9,9 + 2 = -0,24 ⋅ 98,01 + 23,76 + 2 = -23,5224 + 25,76 = 2,2376
Dus de basket hangt op een hoogte van 2,24 meter.
33.
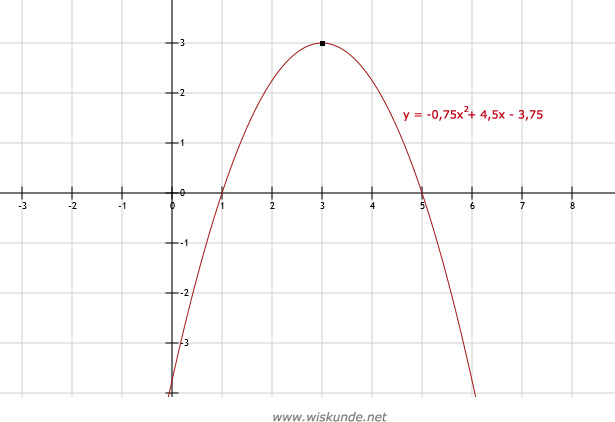
a = -0,75, b = 4,5, c = -3,75
Xtop = -b/2a = -4,5/-1,5 = 3
Ytop = f(Xtop) = f(3) = -0,75 ⋅ (3)2 + 4,5 ⋅ 3 - 3,75 = -0,75 ⋅ 9 + 13,5 - 3,75 = -6,75 + 9,75 = 3
Dus maximale hoogte is 3 meter. Dus top van de parabool is: Top(3,3)
b.
Als de bestelbus een breedte heeft van 2 meter en deze rijdt in het midden van de tunnel dan hebben we te maken met x = 2 en x = 4. Midden van de tunnel is bij x = 3. Want Xtop = 3.
Vul in x = 2 in f: levert:
f(2) = -0,75 ⋅ (2)2 + 4,5 ⋅ 2 - 3,75 = -0,75 ⋅ 4 + 9 - 3,75 = -3 + 9 - 3,75 = 2,25
Op basis van symmetrie is f(4) dan ook gelijk aan 2,25.
Dus de hoogte die erbij hoort is 2,25.
Dus de bestelbus past net. De bus heeft 5 cm over.
Tip:
(-4)2 = -4 ⋅ -4 = 16
-42 = - 4 ⋅ 4 = -16
a.(-4)2 = -4 ⋅ -4 = 16
-42 = - 4 ⋅ 4 = -16
f(4) = (4)2 + 3 = 16 + 3 = 19
f(-4) = (-4)2 + 3 = 16 + 3 = 19
f(0) = (0)2 + 3 = 0 + 3 = 3
b.
De haakjesnotatie van f is f(x) = x2 + 3.
25.
Tip:
Als f(3) = 5 dan ligt het punt (3,5) op de grafiek van f.
a.Als f(3) = 5 dan ligt het punt (3,5) op de grafiek van f.
y = x2 - 4
b.
f(5) = (5)2 - 4 = 25 - 4 = 21
f(-2) = (-2)2 - 4 = 4 - 4 = 0
c.
f(3) = (3)2 - 4 = 9 - 4 = 5
A(3,5) ligt op de grafiek omdat 5 het beeld is van origineel 3.
d.
f(6) = (6)2 - 4 = 36 - 4 = 32
Dus punt (6,32) ligt op de grafiek van f.
26.
Tip:
Als g(5) = -68 dan ligt het punt (5,-68) op de grafiek van g.
a.Als g(5) = -68 dan ligt het punt (5,-68) op de grafiek van g.
g(5) = -3 ⋅ (5)2 + 7 = -3 ⋅ 25 + 7 = -75 + 7 = -68
g(-1) = -3 ⋅ (-1)2 + 7 = -3 ⋅ 1 + 7 = -3 + 7 = 4
b.
g(0) = -3 ⋅ (0)2 + 7 = -3 ⋅ 0 + 7 = 0 + 7 = 7
Dus het punt (0,7) ligt op de grafiek van g.
c.
g(-2) = -3 ⋅ (-2)2 + 7 = -3 ⋅ 4 + 7 = -12 + 7 = -5
Dus het punt (-2,-5) ligt op de grafiek van g.
27.
Tip:
Denk aan de haakjes!
(-2)2 = -2 x -2 = 4
Maar -22 = - 2 x 2 = -4
a.Denk aan de haakjes!
(-2)2 = -2 x -2 = 4
Maar -22 = - 2 x 2 = -4
g(5) = -2 ⋅ (5)2 + 8 ⋅ 5 = -2 ⋅ 25 + 40 = -50 + 40 = -10
g(-3) = -2 ⋅ (-3)2 + 8 ⋅ -3 = -2 ⋅ 9 - 24 = -18 - 24 = -42
b.
y = -2x2 + 8x
c.
g(-1) = -2 ⋅ (-1)2 + 8 ⋅ -1 = -2 ⋅ 1 - 8 = -2 - 8 = -10
Dus het punt P(-1,-10) ligt op de grafiek.
28.
Tip:
Je kunt een grafiek dus opschrijven met een formule of met haakjes notatie.
a.Je kunt een grafiek dus opschrijven met een formule of met haakjes notatie.
h(5) = (5)2 - 7 ⋅ 5 - 5 = 25 - 35 - 5 = -15
h(-4) = (-4)2 - 7 ⋅ -4 - 5 = 16 + 28 - 5 = 39
b.
A(-1,y), dus YA => h(-1) = (-1)2 - 7 ⋅ -1 - 5 = 1 + 7 - 5 = 3
Dus we hebben dan het punt A(-1,3).
c.
B(6,y), dus YB => h(6) = (6)2 - 7 ⋅ 6 - 5 = 36 - 42 - 5 = -11
Dus we hebben dan het punt B(6,-11).
29.
Tip:
Xtop = -b/2a
Ytop = f(Xtop), dus de Xtop invullen in de functie
a.Xtop = -b/2a
Ytop = f(Xtop), dus de Xtop invullen in de functie
a = -1, b = 6, c = -3
Xtop = -b/2a = -6/-2 = 3
Ytop = f(3) = -(3)2 + 6 ⋅ 3 - 3
= -9 + 18 - 3
= 6
Dus de top is: Top(3,6).
b.
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(x) | -10 | -3 | 2 | 5 | 6 | 5 | 2 | -3 | -10 |

30.
Tip:
Als punt A(10,31) op de grafiek ligt, dan moet gelden g(10) = 31.
Bereken dus eerst g(10) en kijk of er 31 uitkomt.
Zoja, dan ligt het punt wel op de grafiek. Anders niet.
a.Als punt A(10,31) op de grafiek ligt, dan moet gelden g(10) = 31.
Bereken dus eerst g(10) en kijk of er 31 uitkomt.
Zoja, dan ligt het punt wel op de grafiek. Anders niet.
a = 0,5, b = 2, c = 1
Xtop = -b/2a = -2/1 = -2
Ytop = g(-2) = 0,5 ⋅ (-2)2 + 2 ⋅ -2 + 1 = 0,5 ⋅ 4 - 4 + 1 = 2 - 4 + 1 = -1
Dus de top is: Top(-2,-1).
b.
g(10) = 0,5 ⋅ (10)2 + 2 ⋅ 10 + 1 = 0,5 ⋅ 100 + 20 + 1 = 50 + 20 + 1 = 71
Dus (10,71) ligt op de grafiek, en dus niet (10,31).
31.
Tip:
Wil het punt P op de grafiek liggen dan moet gelden: h(-10) = -36. Is dat ook zo?
a.Wil het punt P op de grafiek liggen dan moet gelden: h(-10) = -36. Is dat ook zo?
a = -0,5, b = -1, c = 4
Xtop = -b/2a = 1/-1 = -1
Ytop = h(-1) = -0,5 ⋅ (-1)2 - -1 + 4 = -0,5 ⋅ 1 + 1 + 4 = 4½
Dus de top is: Top(-1,4½).
b.
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| h(x) | -3,5 | 0 | 2,5 | 4 | 4,5 | 4 | 2,5 | 0 | -3,5 |
h(-10) = -0,5 ⋅ (-10)2 - -10 + 4 = -0,5 ⋅ 100 + 10 + 4 = -50 + 14 = -36
Dus P(-10,-36) ligt op de grafiek van h.

32.
Tip:
Waar de bal wordt losgelaten, is bij x = 0.
Waar de bal de basket raakt, is bij x = 9,9.
a.Waar de bal wordt losgelaten, is bij x = 0.
Waar de bal de basket raakt, is bij x = 9,9.
a = -0,24, b = 2,4, c = 2
Xtop = -b/2a = -2,4/-0,48 = 5
Ytop = f(5) = -0,24 ⋅ (5)2 + 2,4 ⋅ 5 + 2 = -0,24 ⋅ 25 + 12 + 2 = -6 + 14 = 8
Dus de top is: Top(5,8).
b.
Bereken f(0) levert:
f(0) = -0,24 ⋅ (0)2 + 2,4 ⋅ 0 + 2 = 0 + 0 + 2 = 2
Dus hij laat de bal los op een hoogte van 2 meter.
c.
Bereken f(9,9) levert:
f(9,9) = -0,24 ⋅ (9,9)2 + 2,4 ⋅ 9,9 + 2 = -0,24 ⋅ 98,01 + 23,76 + 2 = -23,5224 + 25,76 = 2,2376
Dus de basket hangt op een hoogte van 2,24 meter.
33.
Tip:
Xtop (dat is de x-coördinaat van de top) ligt precies in het midden van de tunnel op de x-as.
Ytop (dat is de y-coördinaat van de top) is de hoogte van de tunnel.
a.Xtop (dat is de x-coördinaat van de top) ligt precies in het midden van de tunnel op de x-as.
Ytop (dat is de y-coördinaat van de top) is de hoogte van de tunnel.
a = -0,75, b = 4,5, c = -3,75
Xtop = -b/2a = -4,5/-1,5 = 3
Ytop = f(Xtop) = f(3) = -0,75 ⋅ (3)2 + 4,5 ⋅ 3 - 3,75 = -0,75 ⋅ 9 + 13,5 - 3,75 = -6,75 + 9,75 = 3
Dus maximale hoogte is 3 meter. Dus top van de parabool is: Top(3,3)
b.
Als de bestelbus een breedte heeft van 2 meter en deze rijdt in het midden van de tunnel dan hebben we te maken met x = 2 en x = 4. Midden van de tunnel is bij x = 3. Want Xtop = 3.
Vul in x = 2 in f: levert:
f(2) = -0,75 ⋅ (2)2 + 4,5 ⋅ 2 - 3,75 = -0,75 ⋅ 4 + 9 - 3,75 = -3 + 9 - 3,75 = 2,25
Op basis van symmetrie is f(4) dan ook gelijk aan 2,25.
Dus de hoogte die erbij hoort is 2,25.
Dus de bestelbus past net. De bus heeft 5 cm over.

34.
a = 1, b = 4, c = 5
Xtop = -b/2a = -4/2 = -2
b.
Gegeven: Ytop = 12 dus f(Xtop) = 12
f(-2) = (-2)2 + 4 ⋅ -2 + p = 12
4 - 8 + p = 12
-4 + p = 12
p = 16
35.
a = -2, b = -6, c = p
Xtop = -b/2a = - -6/-4 = 6/-4 = -1,5
Ytop = g(-1,5) = -8 (gegeven)
g(-1,5) = -2 ⋅ (-1,5)2 - 6 ⋅ -1,5 + p = -8
-2 ⋅ 2,25 + 9 + p = -8 (een vergelijking met 1 onbekende, dus we kunnen p oplossen)
-4,5 + 9 + p = -8
4,5 + p = -8
p = -12,5
b.
Vul P(2,-6) in h(x) levert:
h(2) = 6
2 ⋅ 4 + 2p + 10 = -6 (een vergelijking met 1 onbekende, dus we kunnen p oplossen)
8 + 2p + 10 = -6
2p + 18 = -6
2p = -24
p = -12
Nu hebben de dus de parabool: h(x) = 2x2 - 12x + 10 met:
a = 2, b = -12, c = 10
Xtop = -b/2a = 12/4 = 3
Ytop = h(Xtop) = 2 ⋅ (3)2 - 12 ⋅ 3 + 10
= 2 ⋅ 9 - 36 + 10
= 18 - 26
= -8
Dus de top is: (3,-8).
Tip:
Ytop = f(Xtop) d.w.z. om de y-waarde van de top te berekenen, moet je de x-waarde van de top invullen in de functie.
a.Ytop = f(Xtop) d.w.z. om de y-waarde van de top te berekenen, moet je de x-waarde van de top invullen in de functie.
a = 1, b = 4, c = 5
Xtop = -b/2a = -4/2 = -2
b.
Gegeven: Ytop = 12 dus f(Xtop) = 12
f(-2) = (-2)2 + 4 ⋅ -2 + p = 12
4 - 8 + p = 12
-4 + p = 12
p = 16
35.
Tip:
Bij a. zie je snel dat je een vergelijking krijgt met 1 onbekende en kunnen we dus p oplossen.
Bij b. vul P(2,-6) in h(x) en dan p oplossen. Bereken daarna pas Xtop en Ytop.
a.Bij a. zie je snel dat je een vergelijking krijgt met 1 onbekende en kunnen we dus p oplossen.
Bij b. vul P(2,-6) in h(x) en dan p oplossen. Bereken daarna pas Xtop en Ytop.
a = -2, b = -6, c = p
Xtop = -b/2a = - -6/-4 = 6/-4 = -1,5
Ytop = g(-1,5) = -8 (gegeven)
g(-1,5) = -2 ⋅ (-1,5)2 - 6 ⋅ -1,5 + p = -8
-2 ⋅ 2,25 + 9 + p = -8 (een vergelijking met 1 onbekende, dus we kunnen p oplossen)
-4,5 + 9 + p = -8
4,5 + p = -8
p = -12,5
b.
Vul P(2,-6) in h(x) levert:
h(2) = 6
2 ⋅ 4 + 2p + 10 = -6 (een vergelijking met 1 onbekende, dus we kunnen p oplossen)
8 + 2p + 10 = -6
2p + 18 = -6
2p = -24
p = -12
Nu hebben de dus de parabool: h(x) = 2x2 - 12x + 10 met:
a = 2, b = -12, c = 10
Xtop = -b/2a = 12/4 = 3
Ytop = h(Xtop) = 2 ⋅ (3)2 - 12 ⋅ 3 + 10
= 2 ⋅ 9 - 36 + 10
= 18 - 26
= -8
Dus de top is: (3,-8).
Andere paragrafen:
3.1. Kwadratische formules (1 t/m 16)
3.2. De top van een parabool (17 t/m 23)
3.3. Kwadratische functies (24 t/m 35)
3.4. Ontbinden in factoren (36 t/m 50)
3.5. Toepassingen van kwadratische vergelijkingen (51 t/m 62)
3.1. Kwadratische formules (1 t/m 16)
3.2. De top van een parabool (17 t/m 23)
3.3. Kwadratische functies (24 t/m 35)
3.4. Ontbinden in factoren (36 t/m 50)
3.5. Toepassingen van kwadratische vergelijkingen (51 t/m 62)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


