TIP: Wil je ook toegang tot meer dan 16.500 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.1 Kwadratische formules HAVO 3
Boek: Getal & Ruimte - Kwadratische problemen HAVO 3 (deel 1) opgaven 1 t/m 16, 2010Wat is een kwadratische formule?
Een kwadratische formule is een formule van de 2e macht. Er zit dus een kwadraat in.
De basisformule is: y = ax2 + bx + c, met a ≠ 0 want anders hebben we te maken met een rechte lijn.
Als a > 0 dan is het een dalparabool
Als a < 0 dan is het een bergparabool
Van een parabool kunnen we de top bepalen en eventueel de snijpunten met de x-as en y-as.
Voorbeelden van een kwadratische formule: y = x2 of y = -0.5x2 + 6x -3
Een kwadratische formule is een formule van de 2e macht. Er zit dus een kwadraat in.
De basisformule is: y = ax2 + bx + c, met a ≠ 0 want anders hebben we te maken met een rechte lijn.
Als a > 0 dan is het een dalparabool
Als a < 0 dan is het een bergparabool
Van een parabool kunnen we de top bepalen en eventueel de snijpunten met de x-as en y-as.
Voorbeelden van een kwadratische formule: y = x2 of y = -0.5x2 + 6x -3
1.
b. *
2.
(-8)2 = 64
(-9)2 = 81
(-12)2 = 144
(-15)2 = 225
(-4)2 = 16
(-25)2 = 625
(-7)2 = 49
3.
b. Neem x = -10 dan: y = 2 ⋅ (-10)2 + 6 = 2 ⋅ 100 + 6 = 200 + 6 = 206
4.
b. Neem x = -4 dan: y = 3 ⋅ (-4)2 - 6 = 3 ⋅ 16 - 6 = 48 - 6 = 42
c. Neem x = -5 dan: y = 3 ⋅ (-5)2 - 6 = 3 ⋅ 25 - 6 = 75 - 6 = 69
d. Neem x = 8 dan: y = 3 ⋅ (8)2 - 6 = 3 ⋅ 64 - 6 = 192 - 6 = 186
5.
b. Neem x = -1 dan: y = -2 ⋅ (-1)2 + 7 = -2 ⋅ 1 + 7 = -2 + 7 = 5
c.
6.
a. Neem x = 4 dan: y = (4)2 + 3 ⋅ 4 - 5 = 16 + 12 - 5 = 28 - 5 = 23
b. Neem x = 5 dan: y = (5)2 + 3 ⋅ 5 - 5 = 25 + 15 - 5 = 40 - 5 = 35
c. Neem x = -3 dan: y = (-3)2 + 3 ⋅ -3 - 5 = 9 - 9 - 5 = -5
7.
b.
c.
(-2,4), (-1,-1), (0,-4), (1,-5), (2,-4), (3,-1) en (4,4)
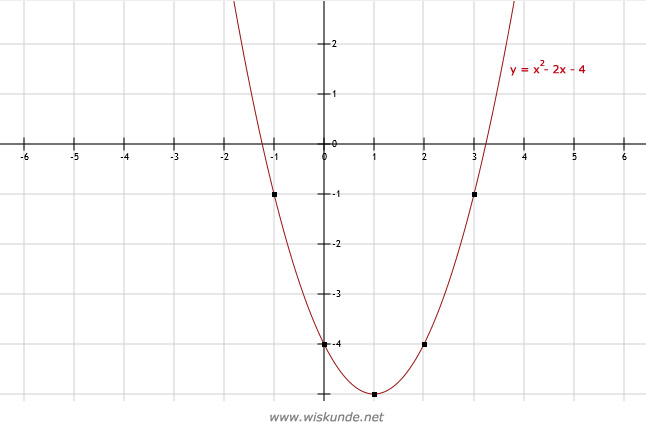
8.
b.
c. Zie afbeelding
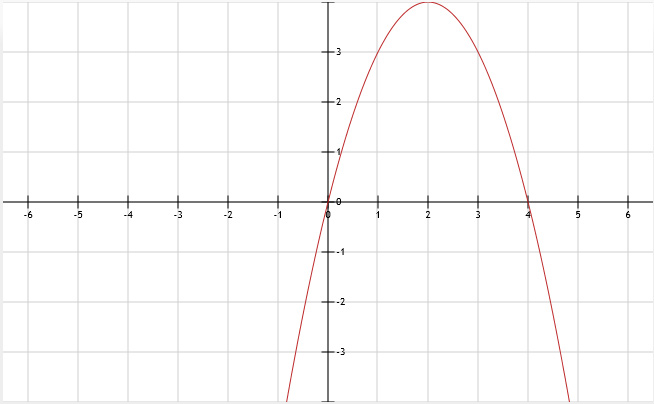
9.
a. Neem x = 4 dan y = 3 ⋅ (4)2 + 2 ⋅ 4 - 4 = 3 ⋅ 16 + 8 - 4 = 48 + 8 - 4 = 52
b. Neem x = 5 dan y = 3 ⋅ (5)2 + 2 ⋅ 5 - 4 = 3 ⋅ 25 + 10 - 4 = 75 + 10 - 4 = 81
c. Neem x = -3 dan y = 3 ⋅ (-3)2 + 2 ⋅ -3 - 4 = 3 ⋅ 9 - 6 - 4 = 27 - 10 = 17
10.
a. y = 2x2 + 6x - 3
b. y = -x2 + 3x
c. y = x2 - x + 8
d. y = 4x2 + 2
e. a = 5, b = -1, c = 1
f. a = -1, b = 8, c = 0
Tip:
42 = 16, dat wil zeggen dat de oppervlakte van een vierkant met zijde 4 gelijk is aan 16.
a.
42 = 16, dat wil zeggen dat de oppervlakte van een vierkant met zijde 4 gelijk is aan 16.
| getal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 20 | 25 |
| kwadraat | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 400 | 625 |
2.
Tip:
Bedenk (-6)2 = -6 ⋅ -6 = 36
Maar: -62 = - 6 ⋅ 6 = -36
Zie de haakjes!
(-6)2 = 36Bedenk (-6)2 = -6 ⋅ -6 = 36
Maar: -62 = - 6 ⋅ 6 = -36
Zie de haakjes!
(-8)2 = 64
(-9)2 = 81
(-12)2 = 144
(-15)2 = 225
(-4)2 = 16
(-25)2 = 625
(-7)2 = 49
3.
Tip:
Zet haakjes om de -10 dus (-10)2
a. Neem x = 3 dan: y = 2 ⋅ (3)2 + 6 = 2 ⋅ 9 + 6 = 18 + 6 = 24Zet haakjes om de -10 dus (-10)2
b. Neem x = -10 dan: y = 2 ⋅ (-10)2 + 6 = 2 ⋅ 100 + 6 = 200 + 6 = 206
4.
Tip:
Het invullen van x = 2 in de formule noemen we substitueren.
a. Neem x = 2 dan: y = 3 ⋅ (2)2 - 6 = 3 ⋅ 4 - 6 = 12 - 6 = 6Het invullen van x = 2 in de formule noemen we substitueren.
b. Neem x = -4 dan: y = 3 ⋅ (-4)2 - 6 = 3 ⋅ 16 - 6 = 48 - 6 = 42
c. Neem x = -5 dan: y = 3 ⋅ (-5)2 - 6 = 3 ⋅ 25 - 6 = 75 - 6 = 69
d. Neem x = 8 dan: y = 3 ⋅ (8)2 - 6 = 3 ⋅ 64 - 6 = 192 - 6 = 186
5.
Tip:
Een kwadraat is altijd positief. Dus een negatief getal in het kwadraat is altijd positief.
a. Neem x = 8 dan: y = -2 ⋅ (8)2 + 7 = -2 ⋅ 64 + 7 = -128 + 7 = -121Een kwadraat is altijd positief. Dus een negatief getal in het kwadraat is altijd positief.
b. Neem x = -1 dan: y = -2 ⋅ (-1)2 + 7 = -2 ⋅ 1 + 7 = -2 + 7 = 5
c.
| x | -3 | -2 | 0 | 3 | 5 |
| y | -11 | -1 | 7 | -11 | -43 |
6.
a. Neem x = 4 dan: y = (4)2 + 3 ⋅ 4 - 5 = 16 + 12 - 5 = 28 - 5 = 23
b. Neem x = 5 dan: y = (5)2 + 3 ⋅ 5 - 5 = 25 + 15 - 5 = 40 - 5 = 35
c. Neem x = -3 dan: y = (-3)2 + 3 ⋅ -3 - 5 = 9 - 9 - 5 = -5
7.
Tip:
Zie je de symmetrie in de tabel bij x = 1?
a.
Vul voor x het getal -2 in. Dit levert: y = (-2)2 - 2 ⋅ -2 - 4 = 4 + 4 - 4 = 4Zie je de symmetrie in de tabel bij x = 1?
b.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 4 | -1 | -4 | -5 | -4 | -1 | 4 |

8.
Tip:
-(-1)2 = -(1) = -1
a.
Vul voor x het getal -1 in. Dit levert: y = -(-1)2 + 4 ⋅ -1 = -(1) + -4 = -1 - 4 = -5-(-1)2 = -(1) = -1
b.
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | -5 | 0 | 3 | 4 | 3 | 0 | -5 |

9.
a. Neem x = 4 dan y = 3 ⋅ (4)2 + 2 ⋅ 4 - 4 = 3 ⋅ 16 + 8 - 4 = 48 + 8 - 4 = 52
b. Neem x = 5 dan y = 3 ⋅ (5)2 + 2 ⋅ 5 - 4 = 3 ⋅ 25 + 10 - 4 = 75 + 10 - 4 = 81
c. Neem x = -3 dan y = 3 ⋅ (-3)2 + 2 ⋅ -3 - 4 = 3 ⋅ 9 - 6 - 4 = 27 - 10 = 17
10.
a. y = 2x2 + 6x - 3
b. y = -x2 + 3x
c. y = x2 - x + 8
d. y = 4x2 + 2
e. a = 5, b = -1, c = 1
f. a = -1, b = 8, c = 0
11.
b. Top is (1,1)
c. *
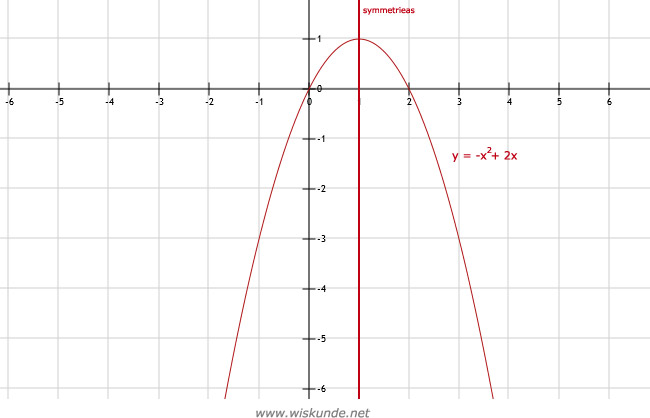
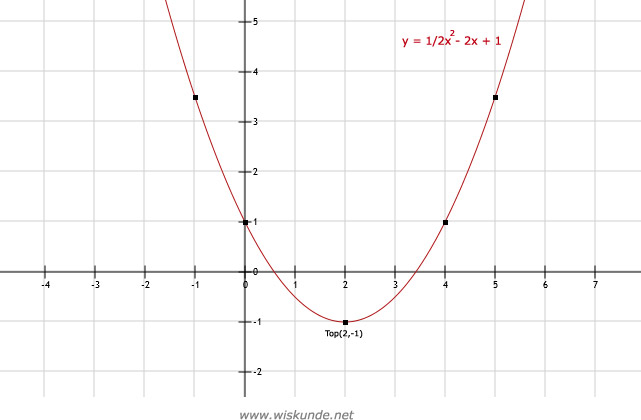
12.
Top is (2,-1)
b. Neem x = 10 dan y = 1/2 ⋅ (10)2 - 2 ⋅ 10 + 1 = 1/2 ⋅ 100 - 20 + 1 = 50 - 20 + 1 = 30 + 1 = 31
Dus punt A(10,31) ligt op de grafiek.
13.
x = 4 invullen, levert: h = -0,05 ⋅ (4)2 + 0,6 ⋅ 4 + 2,1 = -0,05 ⋅ 16 + 2,4 + 2,1 = -0,8 + 4,5 = 3,7
Dus bij x = 4 is de hoogte van de shuttle 3,7 meter.
b.
x = 3 invullen, levert: h = -0,05 ⋅ (3)2 + 0,6 ⋅ 3 + 2,1 = -0,05 ⋅ 9 + 1,8 + 2,1 = -0,45 + 3,9 = 3,45
x = 9 invullen, levert: h = -0,05 ⋅ (9)2 + 0,6 ⋅ 9 + 2,1 = -0,05 ⋅ 81 + 5,4 + 2,1 = -4,05 + 7,5 = 3,45
Dus je ziet dat bij x = 3 en x = 9 de hoogte gelijk is.
c.
De Xtop ligt in het midden van x = 3 en x = 9. Dat is dus bij x = 6.
x = 6 invullen, levert: h = -0,05 ⋅ (6)2 + 0,6 ⋅ 6 + 2,1 = -0,05 ⋅ 36 + 3,6 + 2,1 = -1,8 + 5,7 = 3,9
Dus de top is bij (6 ; 3,9).
d.
x = 14 invullen, levert: h = -0,05 ⋅ (14)2 + 0,6 ⋅ 14 + 2,1 = -0,05 ⋅ 196 + 8,4 + 2,1 = -9,8 + 10,5 = 0,7
Dus bij x = 14 is de hoogte 0,7 meter.
Dus de shuttle is dan nog niet op de grond.
14.
De grootste hoogte zit bij x = 0.
x = 0 invullen, levert: h = -0,125 ⋅ (0)2 + 4 = 0 + 4 = 4
Dus de hoogte van het viaduct is 4 meter.
b.
Als de vrachtwagen 3 meter breed is dan rijdt hij op -1,5 meter en 1,5 meter van de oorsprong als de vrachtwagen precies in het midden rijdt.
Dus kies x = 1,5 en x = -1,5. Dit levert gelijke hoogte op basis van symmetrie.
x = 1,5 invullen, levert: h = -0,125 ⋅ (1,5)2 + 4 = -0,125 ⋅ 2,25 + 4 = -0,28125 + 4 = 3,71875
Dus de hoogte bij de formule is ongeveer 3,72 meter en de vrachtwagen is 3,75 meter hoog. Dus het past niet!
15.
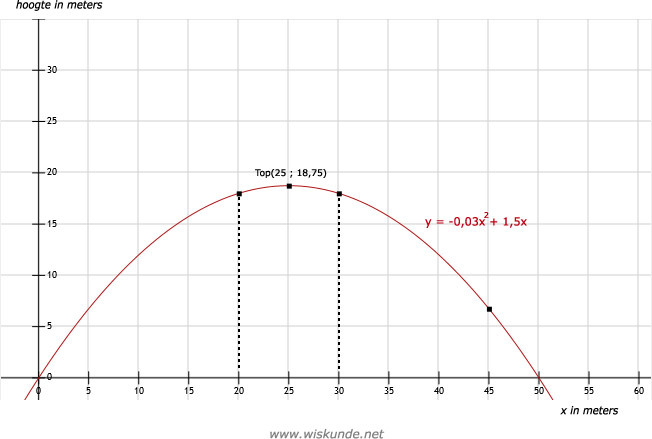
x = 20 invullen, levert: h = -0,03 ⋅ (20)2 + 1,5 ⋅ 20 = -0,03 ⋅ 400 + 30 = -12 + 30 = 18 (meter)
x = 30 invullen, levert: h = -0,03 ⋅ (30)2 + 1,5 ⋅ 30 = -0,03 ⋅ 900 + 45 = -27 + 45 = 18 (meter)
b.
Xtop ligt in het midden van x = 20 en x = 30. Dus Xtop = 25.
x = 25 invullen, levert: h = -0,03 ⋅ (25)2 + 1,5 ⋅ 25 = -0,03 ⋅ 625 + 37,5 = -18,75 + 37,5 = 18,75 (meter)
Dus de maximale hoogte is 18,75 meter bij x = 25 meter (top van de parabool: (25 ; 18,75)).
c.
x = 18 invullen, levert: h = -0,03 ⋅ (18)2 + 1,5 ⋅ 18 = 17,28 (meter)
x = 10 invullen, levert: h = -0,03 ⋅ (10)2 + 1,5 ⋅ 10 = 12 (meter)
Het verschil is dus 17,28 - 12 = 5,28 meter.
d.
x = 45 invullen, levert: h = -0,03 ⋅ (45)2 + 1,5 ⋅ 45 = -0,03 ⋅ 2025 + 67,5 = -60,75 + 67,5 = 6,75 (meter)
Dus bij x = 45 is de hoogte nog 6,75 meter. Dus de bal is bij een grotere x pas op de grond (zie x = 50).
Dus hij trapt de bal verder weg dan 45 meter.
16.
v = 12 invullen, levert: A = 0,05 ⋅ (12)2 + 0,28 ⋅ 12 = 0,05 ⋅ 144 + 3,36 = 7,2 + 3,36 = 10,56 (meter)
v = 20 invullen, levert: A = 0,05 ⋅ (20)2 + 0,28 ⋅ 20 = 0,05 ⋅ 400 + 5,6 = 20 + 5,6 = 25,6 (meter)
Dus de veilige afstand neemt toe met 25,6 - 10,56 = 15,04 meter.
b.
v = 25 invullen, levert: A = 0,05 ⋅ (25)2 + 0,28 ⋅ 25 = 0,05 ⋅ 625 + 7 = 31,25 + 7 = 38,25 (meter)
c.
50 km/uur = 13,89 m/s (delen door 3,6)
v = 13,89 invullen, levert: A = 0,05 ⋅ (13,89)2 + 0,28 ⋅ 13,89 = 9,646605 + 3,8892 ≈ 13,54 (meter)
Bij 50 km/uur is de veilige afstand volgens de formule dus 13,54 meter. Maar Arie had 16 meter nodig. Dus hij reed harder dan 50 km/uur.
Tip:
De top kun je aflezen uit zowel de grafiek als de tabel.
a.
De top kun je aflezen uit zowel de grafiek als de tabel.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -8 | -3 | 0 | 1 | 0 | -3 | -8 |
c. *

12.
Tip:
Wil een punt op de grafiek liggen dan dient dat punt een oplossing te zijn van de formule.
Dus vul het punt in de formule en kijk of het klopt.
a.
Wil een punt op de grafiek liggen dan dient dat punt een oplossing te zijn van de formule.
Dus vul het punt in de formule en kijk of het klopt.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 7 | 3,5 | 1 | -0,5 | -1 | -0,5 | 1 | 3,5 | 7 |
Top is (2,-1)
b. Neem x = 10 dan y = 1/2 ⋅ (10)2 - 2 ⋅ 10 + 1 = 1/2 ⋅ 100 - 20 + 1 = 50 - 20 + 1 = 30 + 1 = 31
Dus punt A(10,31) ligt op de grafiek.

13.
Tip:
Zie dat de boog die de shuttle maakt, lijkt op een parabool. Waar de parabool de x -as snijdt, daar is de hoogte gelijk aan 0 en ligt dus de shuttle op de grond.
a.Zie dat de boog die de shuttle maakt, lijkt op een parabool. Waar de parabool de x -as snijdt, daar is de hoogte gelijk aan 0 en ligt dus de shuttle op de grond.
x = 4 invullen, levert: h = -0,05 ⋅ (4)2 + 0,6 ⋅ 4 + 2,1 = -0,05 ⋅ 16 + 2,4 + 2,1 = -0,8 + 4,5 = 3,7
Dus bij x = 4 is de hoogte van de shuttle 3,7 meter.
b.
x = 3 invullen, levert: h = -0,05 ⋅ (3)2 + 0,6 ⋅ 3 + 2,1 = -0,05 ⋅ 9 + 1,8 + 2,1 = -0,45 + 3,9 = 3,45
x = 9 invullen, levert: h = -0,05 ⋅ (9)2 + 0,6 ⋅ 9 + 2,1 = -0,05 ⋅ 81 + 5,4 + 2,1 = -4,05 + 7,5 = 3,45
Dus je ziet dat bij x = 3 en x = 9 de hoogte gelijk is.
c.
De Xtop ligt in het midden van x = 3 en x = 9. Dat is dus bij x = 6.
x = 6 invullen, levert: h = -0,05 ⋅ (6)2 + 0,6 ⋅ 6 + 2,1 = -0,05 ⋅ 36 + 3,6 + 2,1 = -1,8 + 5,7 = 3,9
Dus de top is bij (6 ; 3,9).
d.
x = 14 invullen, levert: h = -0,05 ⋅ (14)2 + 0,6 ⋅ 14 + 2,1 = -0,05 ⋅ 196 + 8,4 + 2,1 = -9,8 + 10,5 = 0,7
Dus bij x = 14 is de hoogte 0,7 meter.
Dus de shuttle is dan nog niet op de grond.
14.
Tip:
Zie de oorsprong getekend met de x-as en y-as in het plaatje. Bij de oorsprong geldt: x = 0.
a. Zie de oorsprong getekend met de x-as en y-as in het plaatje. Bij de oorsprong geldt: x = 0.
De grootste hoogte zit bij x = 0.
x = 0 invullen, levert: h = -0,125 ⋅ (0)2 + 4 = 0 + 4 = 4
Dus de hoogte van het viaduct is 4 meter.
b.
Als de vrachtwagen 3 meter breed is dan rijdt hij op -1,5 meter en 1,5 meter van de oorsprong als de vrachtwagen precies in het midden rijdt.
Dus kies x = 1,5 en x = -1,5. Dit levert gelijke hoogte op basis van symmetrie.
x = 1,5 invullen, levert: h = -0,125 ⋅ (1,5)2 + 4 = -0,125 ⋅ 2,25 + 4 = -0,28125 + 4 = 3,71875
Dus de hoogte bij de formule is ongeveer 3,72 meter en de vrachtwagen is 3,75 meter hoog. Dus het past niet!
15.
Tip:
We zien bij a. dat de hoogte bij x = 20 en x = 30 gelijk is. Dus er is sprake van symmetrie.
De symmetrieas van de parabool ligt dan in het midden van x = 20 en x = 30. Dus Xtop = 25.
Zie tevens de afbeelding.
a.We zien bij a. dat de hoogte bij x = 20 en x = 30 gelijk is. Dus er is sprake van symmetrie.
De symmetrieas van de parabool ligt dan in het midden van x = 20 en x = 30. Dus Xtop = 25.
Zie tevens de afbeelding.
x = 20 invullen, levert: h = -0,03 ⋅ (20)2 + 1,5 ⋅ 20 = -0,03 ⋅ 400 + 30 = -12 + 30 = 18 (meter)
x = 30 invullen, levert: h = -0,03 ⋅ (30)2 + 1,5 ⋅ 30 = -0,03 ⋅ 900 + 45 = -27 + 45 = 18 (meter)
b.
Xtop ligt in het midden van x = 20 en x = 30. Dus Xtop = 25.
x = 25 invullen, levert: h = -0,03 ⋅ (25)2 + 1,5 ⋅ 25 = -0,03 ⋅ 625 + 37,5 = -18,75 + 37,5 = 18,75 (meter)
Dus de maximale hoogte is 18,75 meter bij x = 25 meter (top van de parabool: (25 ; 18,75)).
c.
x = 18 invullen, levert: h = -0,03 ⋅ (18)2 + 1,5 ⋅ 18 = 17,28 (meter)
x = 10 invullen, levert: h = -0,03 ⋅ (10)2 + 1,5 ⋅ 10 = 12 (meter)
Het verschil is dus 17,28 - 12 = 5,28 meter.
d.
x = 45 invullen, levert: h = -0,03 ⋅ (45)2 + 1,5 ⋅ 45 = -0,03 ⋅ 2025 + 67,5 = -60,75 + 67,5 = 6,75 (meter)
Dus bij x = 45 is de hoogte nog 6,75 meter. Dus de bal is bij een grotere x pas op de grond (zie x = 50).
Dus hij trapt de bal verder weg dan 45 meter.

16.
Tip:
Hoe groter de snelheid (v) hoe langer de veilige afstand moet zijn (A).
Van km/uur naar m/s -> :3,6
Van m/s naar km/uur -> x3,6
a.Hoe groter de snelheid (v) hoe langer de veilige afstand moet zijn (A).
Van km/uur naar m/s -> :3,6
Van m/s naar km/uur -> x3,6
v = 12 invullen, levert: A = 0,05 ⋅ (12)2 + 0,28 ⋅ 12 = 0,05 ⋅ 144 + 3,36 = 7,2 + 3,36 = 10,56 (meter)
v = 20 invullen, levert: A = 0,05 ⋅ (20)2 + 0,28 ⋅ 20 = 0,05 ⋅ 400 + 5,6 = 20 + 5,6 = 25,6 (meter)
Dus de veilige afstand neemt toe met 25,6 - 10,56 = 15,04 meter.
b.
v = 25 invullen, levert: A = 0,05 ⋅ (25)2 + 0,28 ⋅ 25 = 0,05 ⋅ 625 + 7 = 31,25 + 7 = 38,25 (meter)
c.
50 km/uur = 13,89 m/s (delen door 3,6)
v = 13,89 invullen, levert: A = 0,05 ⋅ (13,89)2 + 0,28 ⋅ 13,89 = 9,646605 + 3,8892 ≈ 13,54 (meter)
Bij 50 km/uur is de veilige afstand volgens de formule dus 13,54 meter. Maar Arie had 16 meter nodig. Dus hij reed harder dan 50 km/uur.
Andere paragrafen:
3.1. Kwadratische formules (1 t/m 16)
3.2. De top van een parabool (17 t/m 23)
3.3. Kwadratische functies (24 t/m 35)
3.4. Ontbinden in factoren (36 t/m 50)
3.5. Toepassingen van kwadratische vergelijkingen (51 t/m 62)
3.1. Kwadratische formules (1 t/m 16)
3.2. De top van een parabool (17 t/m 23)
3.3. Kwadratische functies (24 t/m 35)
3.4. Ontbinden in factoren (36 t/m 50)
3.5. Toepassingen van kwadratische vergelijkingen (51 t/m 62)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


