TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.4 Ontbinden in factoren HAVO 3
Boek: Getal & Ruimte - Kwadratische problemen HAVO 3 (deel 1) opgaven 36 t/m 50, 2010Waarom de product-som-methode?
Ontbinden in factoren met de product-som-methode gaat als volgt. Gegeven x2 - 10x + 21.
Zoek twee getallen waarvan het product 21 is en de som -10. Dat zijn de getallen: -3 en -7.
Ontbinden in factoren levert dat: x2 - 10x + 21 = (x - 3)(x - 7)
Zou je (x - 3)(x - 7) met de haakjes-methode weer uitwerken, krijg je uiteraard weer x2 - 10x + 21.
Op deze wijze bepaal je de snijpunten van een parabool met de x-as (x = 3 of x = 7).
Snijpunten x-as: (3,0) en (7,0).
Ontbinden in factoren met de product-som-methode gaat als volgt. Gegeven x2 - 10x + 21.
Zoek twee getallen waarvan het product 21 is en de som -10. Dat zijn de getallen: -3 en -7.
Ontbinden in factoren levert dat: x2 - 10x + 21 = (x - 3)(x - 7)
Zou je (x - 3)(x - 7) met de haakjes-methode weer uitwerken, krijg je uiteraard weer x2 - 10x + 21.
Op deze wijze bepaal je de snijpunten van een parabool met de x-as (x = 3 of x = 7).
Snijpunten x-as: (3,0) en (7,0).
36.
b. x2 - 3x = x(x - 3)
c. x2 - x = x(x - 1)
d. 3x2 + 6x = 3x(x + 2)
37.
b. Zoek 2 getallen met product 15 en som 16: (x + 1)(x + 15)
c. Zoek 2 getallen met product 15 en som -16: (x - 1)(x - 15)
38.
b. x(x + 1)
c. x(5x - 2)
d. 8x(x + 2)
e. x(x - 0,3)
f. 3x(x + 9)
39.
b. (x + 1)(x + 18)
c. (x + 3)(x + 6)
d. (x + 2)(x + 9)
e. (x - 3)(x - 6)
f. (x + 1)(x - 18)
g. (x - 2)(x + 9)
h. (x + 3)(x - 6)
i. x(x - 18)

40.
b. (x - 2)(x + 3)
c. (x + 1)(x + 6)
d. (x - 1)(x + 6)
e. (x - 2)(x - 3)
f. (x + 1)(x - 6)
g. (x + 2)(x - 3)
h. (x - 1)(x - 6)
41.
b. (x + 1)(x + 10)
c. (x + 1)(x - 10)
d. (x + 2)(x - 5)
e. (x + 2)(x - 7)
f. (x - 2)(x + 12)
42.
a. (x + 2)(x - 6)
b. (x + 4)(x - 3)
c. x(x - 4)
d. (x - 1)(x - 20)
e. (x + 2)(x - 10)
f. x(8x - 15)
43.
b. (x - 4)(x + 5)
c. (x + 6)(x - 8)
d. (x + 1)(x - 8)
e. (x + 2)(x - 8)
f. x(x - 6)
44.
x2 - 7x + 10 = 0
(x - 2)(x - 5) = 0
x - 2 = 0 v x - 5 = 0
x = 2 v x = 5
b.
5x2 - 20x = 0
5x(x - 4) = 0
5x = 0 v x - 4 = 0
x = 0 v x = 4
c.
a2 - 8a - 20 = 0
(a + 2)(a - 10) = 0
a + 2 = 0 v a - 10 = 0
a = -2 v a = 10
d.
p2 + p - 20 = 0
(p - 4)(p + 5) = 0
p - 4 = 0 v p + 5 = 0
p = 4 v p = -5
e.
(x + 1)(x - 3) = 0 (is al van de vorm: A x B = 0, dus A = 0 of B = 0)
x + 1 = 0 v x - 3 = 0
x = -1 v x = 3
f.
x2 - 6x + 5 = 0
(x - 1)(x - 5) = 0
x - 1 = 0 v x - 5 = 0
x = 1 v x = 5
g.
x2 + 7x - 8 = 0
(x - 1)(x + 8) = 0
x - 1 = 0 v x + 8 = 0
x = 1 v x = -8
h.
2x2 - 6x = 0
2x(x - 3) = 0
2x = 0 v x - 3 = 0
x = 0 v x = 3
i.
a2 - 0,3a = 0
a(a - 0,3) = 0
a = 0 v a - 0,3 = 0
a = 0 v a = 0,3
45.
x2 - 4x + 4 = 0
(x - 2)(x - 2) = 0
x - 2 = 0 v x - 2 = 0
x = 2 v x = 2
b.
(x + 2)(x - 3) = 0 (is al van de vorm: A x B = 0, dus A = 0 of B = 0)
x + 2 = 0 v x - 3 = 0
x = -2 v x = 3
c.
n2 - 7n - 18 = 0
(n + 2)(n - 9) = 0
n + 2 = 0 v n - 9 = 0
n = -2 v n = 9
d.
k2 - 16k - 36 = 0
(k + 2)(k - 18) = 0
k + 2 = 0 v k - 18 = 0
k = -2 v k = -18
e.
-x2 - 12x = 0 (links en rechts x-1)
x2 + 12x = 0
x(x + 12) = 0
x = 0 v x + 12 = 0
x = 0 v x = -12
f.
a2 - 5a - 3 + 7 = 0
a2 - 5a + 4 = 0
(a - 1)(a - 4) = 0
a - 1 = 0 v a - 4 = 0
a = 1 v a = 4
Tip:
Ontbinden in factoren wil zeggen: schrijf als een product, dus "iets" maal "iets"
In de wiskunde is "som" gelijk aan + en "product" gelijk aan x (lees keer) .
a. x2 + 4x = x(x + 4)Ontbinden in factoren wil zeggen: schrijf als een product, dus "iets" maal "iets"
In de wiskunde is "som" gelijk aan + en "product" gelijk aan x (lees keer) .
b. x2 - 3x = x(x - 3)
c. x2 - x = x(x - 1)
d. 3x2 + 6x = 3x(x + 2)
37.
Tip:
Zie a. het product van 3 en 5 is gelijk aan 3 x 5 = 15
en de som van 3 en 5 is gelijk aan 3 + 5 = 8.
a. Zoek 2 getallen met product 15 en som 8: (x + 3)(x + 5)Zie a. het product van 3 en 5 is gelijk aan 3 x 5 = 15
en de som van 3 en 5 is gelijk aan 3 + 5 = 8.
b. Zoek 2 getallen met product 15 en som 16: (x + 1)(x + 15)
c. Zoek 2 getallen met product 15 en som -16: (x - 1)(x - 15)
38.
Tip:
Bij d. kun je een x voor de haakjes halen, maar sterker nog: je kunt zelf 8x voor de haakjes halen!
Bij f. kun je een x voor de haakjes halen, maar sterker nog: je kunt zelf 3x voor de haakjes halen!
a. x(x + 7)Bij d. kun je een x voor de haakjes halen, maar sterker nog: je kunt zelf 8x voor de haakjes halen!
Bij f. kun je een x voor de haakjes halen, maar sterker nog: je kunt zelf 3x voor de haakjes halen!
b. x(x + 1)
c. x(5x - 2)
d. 8x(x + 2)
e. x(x - 0,3)
f. 3x(x + 9)
39.
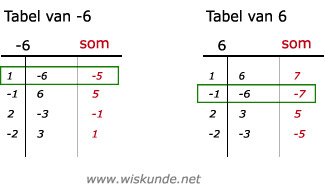
Tip:
Bij opgave b: kijk in de +18 tabel en zoek naar de som van +19. Dus (x + 1)(x + 18), zie groen kader
Bij opgave h: kijk in de -18 tabel en zoek naar de som van -3. Dus (x + 3)(x - 6), zie groen kader
a. Zie afbeeldingBij opgave b: kijk in de +18 tabel en zoek naar de som van +19. Dus (x + 1)(x + 18), zie groen kader
Bij opgave h: kijk in de -18 tabel en zoek naar de som van -3. Dus (x + 3)(x - 6), zie groen kader
b. (x + 1)(x + 18)
c. (x + 3)(x + 6)
d. (x + 2)(x + 9)
e. (x - 3)(x - 6)
f. (x + 1)(x - 18)
g. (x - 2)(x + 9)
h. (x + 3)(x - 6)
i. x(x - 18)

40.
Tip:
Bij opgave f: kijk in de -6 tabel en zoek naar de som van -5. Dus (x + 1)(x - 6), zie groen kader
Bij opgave h: kijk in de +6 tabel en zoek naar de som van -7. Dus (x - 1)(x - 6), zie groen kader
a. Zie afbeeldingBij opgave f: kijk in de -6 tabel en zoek naar de som van -5. Dus (x + 1)(x - 6), zie groen kader
Bij opgave h: kijk in de +6 tabel en zoek naar de som van -7. Dus (x - 1)(x - 6), zie groen kader
b. (x - 2)(x + 3)
c. (x + 1)(x + 6)
d. (x - 1)(x + 6)
e. (x - 2)(x - 3)
f. (x + 1)(x - 6)
g. (x + 2)(x - 3)
h. (x - 1)(x - 6)

41.
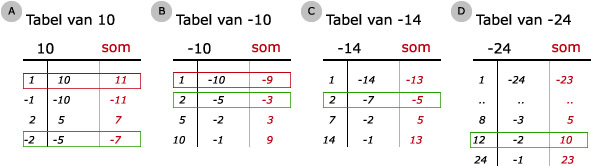
Tip:
Bij a: Zoek 2 getallen waarvan het product gelijk is aan 10 en de som gelijk is aan -7. Zie (A) groen kader.
a. (x - 2)(x - 5)Bij a: Zoek 2 getallen waarvan het product gelijk is aan 10 en de som gelijk is aan -7. Zie (A) groen kader.
b. (x + 1)(x + 10)
c. (x + 1)(x - 10)
d. (x + 2)(x - 5)
e. (x + 2)(x - 7)
f. (x - 2)(x + 12)

42.
a. (x + 2)(x - 6)
b. (x + 4)(x - 3)
c. x(x - 4)
d. (x - 1)(x - 20)
e. (x + 2)(x - 10)
f. x(8x - 15)
43.
Tip:
x2 - x - 2 => er staat een -1 voor de x.
a. (x + 1)(x - 2)x2 - x - 2 => er staat een -1 voor de x.
b. (x - 4)(x + 5)
c. (x + 6)(x - 8)
d. (x + 1)(x - 8)
e. (x + 2)(x - 8)
f. x(x - 6)
44.
Tip:
Controleer of je antwoord klopt door de x in te vullen in de vergelijking.
Er moet dan een ware bewering staan. Dus niet: 3 = 7 want dat is niet waar!
0 = 0 is natuurlijk wel waar.
a. Controleer of je antwoord klopt door de x in te vullen in de vergelijking.
Er moet dan een ware bewering staan. Dus niet: 3 = 7 want dat is niet waar!
0 = 0 is natuurlijk wel waar.
x2 - 7x + 10 = 0
(x - 2)(x - 5) = 0
x - 2 = 0 v x - 5 = 0
x = 2 v x = 5
b.
5x2 - 20x = 0
5x(x - 4) = 0
5x = 0 v x - 4 = 0
x = 0 v x = 4
c.
a2 - 8a - 20 = 0
(a + 2)(a - 10) = 0
a + 2 = 0 v a - 10 = 0
a = -2 v a = 10
d.
p2 + p - 20 = 0
(p - 4)(p + 5) = 0
p - 4 = 0 v p + 5 = 0
p = 4 v p = -5
e.
(x + 1)(x - 3) = 0 (is al van de vorm: A x B = 0, dus A = 0 of B = 0)
x + 1 = 0 v x - 3 = 0
x = -1 v x = 3
f.
x2 - 6x + 5 = 0
(x - 1)(x - 5) = 0
x - 1 = 0 v x - 5 = 0
x = 1 v x = 5
g.
x2 + 7x - 8 = 0
(x - 1)(x + 8) = 0
x - 1 = 0 v x + 8 = 0
x = 1 v x = -8
h.
2x2 - 6x = 0
2x(x - 3) = 0
2x = 0 v x - 3 = 0
x = 0 v x = 3
i.
a2 - 0,3a = 0
a(a - 0,3) = 0
a = 0 v a - 0,3 = 0
a = 0 v a = 0,3
45.
Tip:
Schrijf altijd naar de vorm x2 + ...x + ... = 0
Dus op nul herleiden, d.w.z dat er rechts moet staan ' = 0'.
a. Schrijf altijd naar de vorm x2 + ...x + ... = 0
Dus op nul herleiden, d.w.z dat er rechts moet staan ' = 0'.
x2 - 4x + 4 = 0
(x - 2)(x - 2) = 0
x - 2 = 0 v x - 2 = 0
x = 2 v x = 2
b.
(x + 2)(x - 3) = 0 (is al van de vorm: A x B = 0, dus A = 0 of B = 0)
x + 2 = 0 v x - 3 = 0
x = -2 v x = 3
c.
n2 - 7n - 18 = 0
(n + 2)(n - 9) = 0
n + 2 = 0 v n - 9 = 0
n = -2 v n = 9
d.
k2 - 16k - 36 = 0
(k + 2)(k - 18) = 0
k + 2 = 0 v k - 18 = 0
k = -2 v k = -18
e.
-x2 - 12x = 0 (links en rechts x-1)
x2 + 12x = 0
x(x + 12) = 0
x = 0 v x + 12 = 0
x = 0 v x = -12
f.
a2 - 5a - 3 + 7 = 0
a2 - 5a + 4 = 0
(a - 1)(a - 4) = 0
a - 1 = 0 v a - 4 = 0
a = 1 v a = 4
46.
x(x + 4) = 12 (haakjes wegwerken)
x2 + 4x = 12
x2 + 4x - 12 = 0
(x - 2)(x + 6) = 0
x - 2 = 0 v x + 6 = 0
x = 2 v x = -6
b.
Want deze is al van de vorm A x B = 0, want we weten: Als A x B = 0, dan A = 0 of B = 0
47.
x(x + 3) = 10
x2 + 3x - 10 = 0
(x - 2)(x + 5) = 0
x - 2 = 0 v x + 5 = 0
x = 2 v x = -5
b.
a(a - 1) = 4a
a2 - a = 4a
a2 - 5a = 0
a(a - 5) = 0
a = 0 v a - 5 = 0
a = 0 v a = 5
c.
x(x + 3) = 2x + 6
x2 + 3x = 2x + 6
x2 + x - 6 = 0
(x - 2)(x + 3) = 0
x - 2 = 0 v x + 3 = 0
x = 2 v x = -3
d.
x(x + 4) = -4
x2 + 4x = -4
x2 + 4x + 4 = 0
(x + 2)(x + 2) = 0
x + 2 = 0 v x + 2 = 0
x = -2 v x = -2
e.
p2 = 3(p + 6)
p2 = 3p + 18
p2 - 3p - 18 = 0
(p + 3)(p - 6) = 0
p + 3 = 0 v p - 6 = 0
p = -3 v p = 6
f.
(q - 7)(q + 3) = 24
q2 + 3q - 7q - 21 = 24
q2 - 4q - 45 = 0
(q + 5)(q - 9) = 0
q + 5 = 0 v q - 9 = 0
q = -5 v q = 9
48.
x(x + 1) = 2x + 2
x2 + x = 2x + 2
x2 - x - 2 = 0
(x + 1)(x - 2) = 0
x + 1 = 0 v x - 2 = 0
x = -1 v x = 2
b.
(x - 1)(x + 2) = 10
x2 + 2x - x - 2 = 10
x2 + x - 12 = 0
(x - 3)(x + 4) = 0
x - 3 = 0 v x + 4 = 0
x = 3 v x = -4
c.
(x + 3)2 = 2x + 9
x2 + 6x + 9 = 2x + 9 (links en rechts 9 wegstrepen)
x2 + 6x - 2x = 0
x2 + 4x = 0
x(x + 4) = 0
x = 0 v x + 4 = 0
x = 0 v x = -4
d.
(3x - 1)(2x + 6) = 0
3x - 1 = 0 v 2x + 6 = 0
3x = 1 v 2x = -6
x = 1/3 v x = -3
e.
(3p - 1)(2p + 6) = -6
6p2 + 18p - 2p - 6 = -6 (links en rechts -6 wegstrepen)
6p2 + 16p = 0
p(6p + 16) = 0
p = 0 v 6p + 16 = 0
p = 0 v 6p = -16
p = 0 v p = -16/6 = -8/3 = -2 2/3
f.
(t + 1)(t - 8) = 22
t2 - 8t + t - 8 = 22
t2 - 7t - 30 = 0
(t + 3)(t - 10) = 0
t + 3 = 0 v t - 10 = 0
t = -3 v t = 10
49.
4x2 + 8x - 12 = 0 (links en rechts :4)
x2 + 2x - 3 = 0
(x - 1)(x + 3) = 0
x - 1 = 0 v x + 3 = 0
x = 1 v x = -3
b.
1/2x2 = 5x - 8
1/2x2 - 5x + 8 = 0 (links en rechts x2)
x2 - 10x + 16 = 0
(x - 2)(x - 8) = 0
x - 2 = 0 v x - 8 = 0
x = 2 v x = 8
c.
3a + 10 = a2
a2 - 3a - 10 = 0
(a + 2)(a - 5) = 0
a + 2 = 0 v a - 5 = 0
a = -2 v a = 5
d.
-0,5x2 + 0,5x + 6 = 0 (links en rechts x-2)
x2 - x - 12 = 0
(x + 3)(x - 4) = 0
x + 3 = 0 v x - 4 = 0
x = -3 v x = 4
50.
100k2 - 4900k - 5000 = 0 (links en rechts :100)
k2 - 49k - 50 = 0 (product-som-methode met -50)
(k + 1)(k - 50) = 0
k + 1 = 0 v k - 50 = 0
k = -1 v k = 50
b.
(x - 2)(2x - 5) = x + 2
2x2 - 5x - 4x + 10 = x + 2
2x2 - 9x + 10 = x + 2
2x2 - 10x + 8 = 0 (links en rechts :2)
x2 - 5x + 4 = 0 (product-som-methode met +4)
(x - 1)(x - 4) = 0
x - 1 = 0 v x - 4 = 0
x = 1 v x = 4
c.
(x - 5)2 = 4 - 2(3 - x)
x2 - 10x + 25 = 4 - 6 + 2x
x2 - 10x + 25 = -2 + 2x
x2 - 12x + 27 = 0 (product-som-methode met +27)
(x - 3)(x - 9) = 0
x - 3 = 0 v x - 9 = 0
x = 3 v x = 9
d.
(2x - 1)(2x + 5) = 0
2x - 1 = 0 v 2x + 5 = 0
2x = 1 v 2x = -5
x = 1/2 v x = -5/2 = -2½
e.
(3x + 1)(x - 6) = 3x2
3x2 - 18x + x - 6 = 3x2 (links en rechts 3x2 wegstrepen)
-18x + x - 6 = 0
-17x = 6
x = -6/17
f.
-1/3x2 = x - 6 (links en rechts maal -3 om breuk weg te werken)
x2 = -3x + 18
x2 + 3x - 18 = 0 (product-som-methode met -18)
(x - 3)(x + 6) = 0
x - 3 = 0 v x + 6 = 0
x = 3 v x = -6
Tip:
x(x + 4) = 12
Deze is niet van de vorm x(x + 4) = 0
Dus niet van de vorm A x B = 0, want er staat een 12 i.p.v. een 0.
Dus werk eerst de haakjes weg!
a.x(x + 4) = 12
Deze is niet van de vorm x(x + 4) = 0
Dus niet van de vorm A x B = 0, want er staat een 12 i.p.v. een 0.
Dus werk eerst de haakjes weg!
x(x + 4) = 12 (haakjes wegwerken)
x2 + 4x = 12
x2 + 4x - 12 = 0
(x - 2)(x + 6) = 0
x - 2 = 0 v x + 6 = 0
x = 2 v x = -6
b.
Want deze is al van de vorm A x B = 0, want we weten: Als A x B = 0, dan A = 0 of B = 0
47.
Tip:
Schrijf altijd naar de vorm x2 + ...x + ... = 0
Dus op nul herleiden, d.w.z dat er rechts moet staan ' = 0'.
Of haal een factor voor de haakjes, zoals bij b.
a. Schrijf altijd naar de vorm x2 + ...x + ... = 0
Dus op nul herleiden, d.w.z dat er rechts moet staan ' = 0'.
Of haal een factor voor de haakjes, zoals bij b.
x(x + 3) = 10
x2 + 3x - 10 = 0
(x - 2)(x + 5) = 0
x - 2 = 0 v x + 5 = 0
x = 2 v x = -5
b.
a(a - 1) = 4a
a2 - a = 4a
a2 - 5a = 0
a(a - 5) = 0
a = 0 v a - 5 = 0
a = 0 v a = 5
c.
x(x + 3) = 2x + 6
x2 + 3x = 2x + 6
x2 + x - 6 = 0
(x - 2)(x + 3) = 0
x - 2 = 0 v x + 3 = 0
x = 2 v x = -3
d.
x(x + 4) = -4
x2 + 4x = -4
x2 + 4x + 4 = 0
(x + 2)(x + 2) = 0
x + 2 = 0 v x + 2 = 0
x = -2 v x = -2
e.
p2 = 3(p + 6)
p2 = 3p + 18
p2 - 3p - 18 = 0
(p + 3)(p - 6) = 0
p + 3 = 0 v p - 6 = 0
p = -3 v p = 6
f.
(q - 7)(q + 3) = 24
q2 + 3q - 7q - 21 = 24
q2 - 4q - 45 = 0
(q + 5)(q - 9) = 0
q + 5 = 0 v q - 9 = 0
q = -5 v q = 9
48.
Tip:
Werk eerst de haakjes weg.
Bij d: deze is al goed ontbonden in factoren, dus je kunt meteen gebruiken: Als A x B = 0 dan A = 0 of B = 0
a. Werk eerst de haakjes weg.
Bij d: deze is al goed ontbonden in factoren, dus je kunt meteen gebruiken: Als A x B = 0 dan A = 0 of B = 0
x(x + 1) = 2x + 2
x2 + x = 2x + 2
x2 - x - 2 = 0
(x + 1)(x - 2) = 0
x + 1 = 0 v x - 2 = 0
x = -1 v x = 2
b.
(x - 1)(x + 2) = 10
x2 + 2x - x - 2 = 10
x2 + x - 12 = 0
(x - 3)(x + 4) = 0
x - 3 = 0 v x + 4 = 0
x = 3 v x = -4
c.
(x + 3)2 = 2x + 9
x2 + 6x + 9 = 2x + 9 (links en rechts 9 wegstrepen)
x2 + 6x - 2x = 0
x2 + 4x = 0
x(x + 4) = 0
x = 0 v x + 4 = 0
x = 0 v x = -4
d.
(3x - 1)(2x + 6) = 0
3x - 1 = 0 v 2x + 6 = 0
3x = 1 v 2x = -6
x = 1/3 v x = -3
e.
(3p - 1)(2p + 6) = -6
6p2 + 18p - 2p - 6 = -6 (links en rechts -6 wegstrepen)
6p2 + 16p = 0
p(6p + 16) = 0
p = 0 v 6p + 16 = 0
p = 0 v 6p = -16
p = 0 v p = -16/6 = -8/3 = -2 2/3
f.
(t + 1)(t - 8) = 22
t2 - 8t + t - 8 = 22
t2 - 7t - 30 = 0
(t + 3)(t - 10) = 0
t + 3 = 0 v t - 10 = 0
t = -3 v t = 10
49.
Tip:
Zorg ervoor dat er een x2 staat aan het begin. Vereenvoudig de vergelijking door links en rechts met hetzelfde getal te delen of te vermenigvuldigen.
a. Zorg ervoor dat er een x2 staat aan het begin. Vereenvoudig de vergelijking door links en rechts met hetzelfde getal te delen of te vermenigvuldigen.
4x2 + 8x - 12 = 0 (links en rechts :4)
x2 + 2x - 3 = 0
(x - 1)(x + 3) = 0
x - 1 = 0 v x + 3 = 0
x = 1 v x = -3
b.
1/2x2 = 5x - 8
1/2x2 - 5x + 8 = 0 (links en rechts x2)
x2 - 10x + 16 = 0
(x - 2)(x - 8) = 0
x - 2 = 0 v x - 8 = 0
x = 2 v x = 8
c.
3a + 10 = a2
a2 - 3a - 10 = 0
(a + 2)(a - 5) = 0
a + 2 = 0 v a - 5 = 0
a = -2 v a = 5
d.
-0,5x2 + 0,5x + 6 = 0 (links en rechts x-2)
x2 - x - 12 = 0
(x + 3)(x - 4) = 0
x + 3 = 0 v x - 4 = 0
x = -3 v x = 4
50.
Tip:
Bij d: deze is al goed ontbonden in factoren, dus je kunt meteen gebruiken: Als A x B = 0 dan A = 0 of B = 0
a.Bij d: deze is al goed ontbonden in factoren, dus je kunt meteen gebruiken: Als A x B = 0 dan A = 0 of B = 0
100k2 - 4900k - 5000 = 0 (links en rechts :100)
k2 - 49k - 50 = 0 (product-som-methode met -50)
(k + 1)(k - 50) = 0
k + 1 = 0 v k - 50 = 0
k = -1 v k = 50
b.
(x - 2)(2x - 5) = x + 2
2x2 - 5x - 4x + 10 = x + 2
2x2 - 9x + 10 = x + 2
2x2 - 10x + 8 = 0 (links en rechts :2)
x2 - 5x + 4 = 0 (product-som-methode met +4)
(x - 1)(x - 4) = 0
x - 1 = 0 v x - 4 = 0
x = 1 v x = 4
c.
(x - 5)2 = 4 - 2(3 - x)
x2 - 10x + 25 = 4 - 6 + 2x
x2 - 10x + 25 = -2 + 2x
x2 - 12x + 27 = 0 (product-som-methode met +27)
(x - 3)(x - 9) = 0
x - 3 = 0 v x - 9 = 0
x = 3 v x = 9
d.
(2x - 1)(2x + 5) = 0
2x - 1 = 0 v 2x + 5 = 0
2x = 1 v 2x = -5
x = 1/2 v x = -5/2 = -2½
e.
(3x + 1)(x - 6) = 3x2
3x2 - 18x + x - 6 = 3x2 (links en rechts 3x2 wegstrepen)
-18x + x - 6 = 0
-17x = 6
x = -6/17
f.
-1/3x2 = x - 6 (links en rechts maal -3 om breuk weg te werken)
x2 = -3x + 18
x2 + 3x - 18 = 0 (product-som-methode met -18)
(x - 3)(x + 6) = 0
x - 3 = 0 v x + 6 = 0
x = 3 v x = -6
Andere paragrafen:
3.1. Kwadratische formules (1 t/m 16)
3.2. De top van een parabool (17 t/m 23)
3.3. Kwadratische functies (24 t/m 35)
3.4. Ontbinden in factoren (36 t/m 50)
3.5. Toepassingen van kwadratische vergelijkingen (51 t/m 62)
3.1. Kwadratische formules (1 t/m 16)
3.2. De top van een parabool (17 t/m 23)
3.3. Kwadratische functies (24 t/m 35)
3.4. Ontbinden in factoren (36 t/m 50)
3.5. Toepassingen van kwadratische vergelijkingen (51 t/m 62)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


