TIP: Wil je ook toegang tot meer dan 16.500 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.2 De top van een parabool HAVO 3
Boek: Getal & Ruimte - Kwadratische problemen HAVO 3 (deel 1) opgaven 17 t/m 23, 2010De algemene vergelijking van een parabool is: y = ax2 + bx + c.
Om de top van een parabool te berekenen, gaan we als volgt te werk:
Xtop = -b / 2a
Ytop krijgen we door de Xtop in te vullen in de vergelijking.
Om de top van een parabool te berekenen, gaan we als volgt te werk:
Xtop = -b / 2a
Ytop krijgen we door de Xtop in te vullen in de vergelijking.
17.
b.
Xb = 6
c.
Xtop ligt tuseen (0,0) en (XB,0). Dus Xtop = Xb/2
d.
Xtop = 6/2 = 3
Ytop = (3)2 - 6 ⋅ 3 = 9 - 18 = -9
18.
b. Je moet dan 4 omhoog.
c. De x-coördinaten van de toppen zijn gelijk.
19.
a = 1, b = 4, c = 1
Xtop = -b / 2a = -4/2 = -2
Ytop => y = (-2)2 + 4 ⋅ -2 + 1 = 4 - 8 + 1 = -3
Dus de top van deze parabool is: Top(-2,-3)
b.
a = -1, b = 2, c = 10
Xtop = -b / 2a = -2/-2 = 1
Ytop => y = -(1)2 + 2 ⋅ 1 + 10 = -1 + 2 + 10 = 11
Dus de top van deze parabool is: Top(1,11)
c.
a = 1,2, b = -8,4, c = 1,3
Xtop = -b / 2a = 8,4/2,4 = 3,5
Ytop => y = 1,2 ⋅ (3,5)2 - 8,4 ⋅ 3,5 + 1,3 = 14,7 - 29,4 + 1,3 = -13,4
Dus de top van deze parabool is: Top(3,5 ; -13,4)
d.
a = -0,25, b = 4, c = -17
Xtop = -b / 2a = -4/-0,5 = 8
Ytop => y = -0,25 ⋅ (8)2 + 4 ⋅ 8 - 17 = -0,25 ⋅ 64 + 32 - 17 = -16 + 32 - 17 = -1
Dus de top van deze parabool is: Top(8,-1)
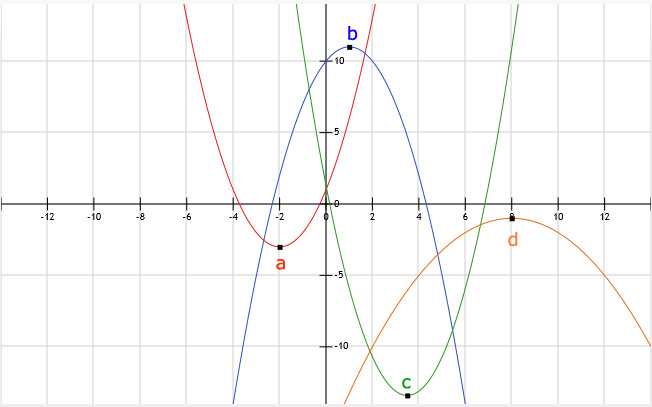
20.
a.
a = 1, b = 12, c = 0
Xtop = -b / 2a = -12/2 = -6
Ytop => y = (-6)2 + 12 ⋅ -6 = 36 - 72 = -36
Dus de top van deze parabool is: Top(-6,-36)
b.
a = -1, b = -1, c = 0
Xtop = -b / 2a = 1/-2 = -0,5
Ytop => y = -(-0,5)2 - -0,5 = -0,25 + 0,5 = 0,25
Dus de top van deze parabool is: Top(-0,5 ; 0,25)
c.
a = 0,02, b = 6, c = 8
Xtop = -b / 2a = -6/0,04 = -150
Ytop => y = 0,02 ⋅ (-150)2 + 6 ⋅ -150 + 8 = 450 - 900 + 8 = -442
Dus de top van deze parabool is: Top(-150,-442)
d.
a = -0,8, b = 16, c = -170
Xtop = -b / 2a = -16/-1,6 = 10
Ytop => y = -0,8 ⋅ (10)2 + 16 ⋅ 10 - 170 = -80 + 160 - 170 = -90
Dus de top van deze parabool is: Top(10,-90)
21.
Vul in a = 10 levert:
W = -5 ⋅ (10)2 + 300 ⋅ 10
= -5 ⋅ 100 + 3000
= -500 + 3000
= 2500
Dus de winst bij 10 grasmaaiers is €2500,-.
b.
a = -5, b = 300, c = 0
Atop = -b/2a
= -300/-10 = 30 (normaal Xtop)
Wtop = -5 ⋅ (30)2 + 300 ⋅ 30 (normaal Ytop)
= -5 ⋅ 900 + 9000
= -4500 + 9000
= 4500
Dus de top van de parabool is: Top(30,4500).
c.
De top is (30,4500) en het is een bergparabool (a<0).
Dus de winst is maximaal bij 30 grasmaaiers.
Deze winst is dan €4500,-.
22.
a = -0,05, b = 1,2, c = 2
Atop = -b/2a
= -1,2/-0,1 = 12 (normaal Xtop)
htop = h(12) = -0,05 ⋅ (12)2 + 1,2 ⋅ 12 + 2
= -0,05 ⋅ 144 + 14,4 + 2
= -7,2 + 16,4
= 9,2
Dus de top is (12 ; 9,2).
b.
Het is een bergparabool met a < 0.
De maximale hoogte is dus 9,2 meter.
c.
h(26) = -0,05 ⋅ (26)2 + 1,2 ⋅ 26 + 2
= -0,05 ⋅ 676 + 31,2 + 2
= -33,8 + 33,2
= -0,6
Dus bij a = 26 is de hoogte negatief.
Dus de speer raakt de grond al eerder.
Dus Anne gooit de speer minder dan 26 meter.
23.
t = 6 invullen, levert:
T = -0,05 ⋅ (6)2 + 1,5 ⋅ 6
T = -0,05 ⋅ 36 + 9
T = -1,8 + 9
T = 7,2
Dus bij t = 6 (om 06:00) is de temperatuur 7,2º.
t = 18 invullen, levert:
T = -0,05 ⋅ (18)2 + 1,5 ⋅ 18
T = -0,05 ⋅ 324 + 27
T = -16,2 + 27
T = 10,8
Dus bij t = 18 (om 18:00) is de temperatuur 10,8º.
b.
Bereken dus de Xtop of in dit geval de ttop.
a = -0,05, b = 1,5, c = 0
Xtop = ttop = -b/2a = -1,5/-0,1 = 15
Dus bij t = 15 (om 15:00) is de temperatuur maximaal.
c.
Maximale temperatuur = Ytop = Ttop =
T(15) = -0,05 ⋅ (15)2 + 1,5 ⋅ 15
= -0,05 ⋅ 225 + 22,5
= -11,25 + 22,5
= 11,25
Dus om 15:00 is de maximale temperatuur gelijk aan 11,25º.
Tip:
Je ziet in de tabel dat de Xtop bij x = 3 zit.
Gegeven een punt B(6,0). Dan geldt:
XB: x-coördinaat van B is gelijk aan 6
YB: y-coördinaat van B is gelijk aan 0
a.Je ziet in de tabel dat de Xtop bij x = 3 zit.
Gegeven een punt B(6,0). Dan geldt:
XB: x-coördinaat van B is gelijk aan 6
YB: y-coördinaat van B is gelijk aan 0
| x | -2 | 0 | 2 | 4 | 6 | 8 |
| y | 16 | 0 | -8 | -8 | 0 | 16 |
Xb = 6
c.
Xtop ligt tuseen (0,0) en (XB,0). Dus Xtop = Xb/2
d.
Xtop = 6/2 = 3
Ytop = (3)2 - 6 ⋅ 3 = 9 - 18 = -9
18.
Tip:
Bij een verticale verschuiving van een parabool blijft de Xtop gelijk.
a. Je moet dan 3 naar beneden.Bij een verticale verschuiving van een parabool blijft de Xtop gelijk.
b. Je moet dan 4 omhoog.
c. De x-coördinaten van de toppen zijn gelijk.
19.
Tip:
Schrijf eerst op wat de a, b en c zijn en gebruik dan -b/2a.
a.Schrijf eerst op wat de a, b en c zijn en gebruik dan -b/2a.
a = 1, b = 4, c = 1
Xtop = -b / 2a = -4/2 = -2
Ytop => y = (-2)2 + 4 ⋅ -2 + 1 = 4 - 8 + 1 = -3
Dus de top van deze parabool is: Top(-2,-3)
b.
a = -1, b = 2, c = 10
Xtop = -b / 2a = -2/-2 = 1
Ytop => y = -(1)2 + 2 ⋅ 1 + 10 = -1 + 2 + 10 = 11
Dus de top van deze parabool is: Top(1,11)
c.
a = 1,2, b = -8,4, c = 1,3
Xtop = -b / 2a = 8,4/2,4 = 3,5
Ytop => y = 1,2 ⋅ (3,5)2 - 8,4 ⋅ 3,5 + 1,3 = 14,7 - 29,4 + 1,3 = -13,4
Dus de top van deze parabool is: Top(3,5 ; -13,4)
d.
a = -0,25, b = 4, c = -17
Xtop = -b / 2a = -4/-0,5 = 8
Ytop => y = -0,25 ⋅ (8)2 + 4 ⋅ 8 - 17 = -0,25 ⋅ 64 + 32 - 17 = -16 + 32 - 17 = -1
Dus de top van deze parabool is: Top(8,-1)

20.
a.
a = 1, b = 12, c = 0
Xtop = -b / 2a = -12/2 = -6
Ytop => y = (-6)2 + 12 ⋅ -6 = 36 - 72 = -36
Dus de top van deze parabool is: Top(-6,-36)
b.
a = -1, b = -1, c = 0
Xtop = -b / 2a = 1/-2 = -0,5
Ytop => y = -(-0,5)2 - -0,5 = -0,25 + 0,5 = 0,25
Dus de top van deze parabool is: Top(-0,5 ; 0,25)
c.
a = 0,02, b = 6, c = 8
Xtop = -b / 2a = -6/0,04 = -150
Ytop => y = 0,02 ⋅ (-150)2 + 6 ⋅ -150 + 8 = 450 - 900 + 8 = -442
Dus de top van deze parabool is: Top(-150,-442)
d.
a = -0,8, b = 16, c = -170
Xtop = -b / 2a = -16/-1,6 = 10
Ytop => y = -0,8 ⋅ (10)2 + 16 ⋅ 10 - 170 = -80 + 160 - 170 = -90
Dus de top van deze parabool is: Top(10,-90)
21.
Tip:
Xtop = -b/2a
Schrijf eerst op wat de a, b en c zijn. De 'a' staat voor de x-kwadraat en de 'b' staat voor de x.
Normaal hebben we een x-as en een y-as. In deze opgave nu een a-as en een W-as.
a.Xtop = -b/2a
Schrijf eerst op wat de a, b en c zijn. De 'a' staat voor de x-kwadraat en de 'b' staat voor de x.
Normaal hebben we een x-as en een y-as. In deze opgave nu een a-as en een W-as.
Vul in a = 10 levert:
W = -5 ⋅ (10)2 + 300 ⋅ 10
= -5 ⋅ 100 + 3000
= -500 + 3000
= 2500
Dus de winst bij 10 grasmaaiers is €2500,-.
b.
a = -5, b = 300, c = 0
Atop = -b/2a
= -300/-10 = 30 (normaal Xtop)
Wtop = -5 ⋅ (30)2 + 300 ⋅ 30 (normaal Ytop)
= -5 ⋅ 900 + 9000
= -4500 + 9000
= 4500
Dus de top van de parabool is: Top(30,4500).
c.
De top is (30,4500) en het is een bergparabool (a<0).
Dus de winst is maximaal bij 30 grasmaaiers.
Deze winst is dan €4500,-.
22.
Tip:
Top is normaal van de vorm (x,y). In deze opgave van de vorm (a,h). Dat komt omdat de functie in a en h is geschreven.
a.Top is normaal van de vorm (x,y). In deze opgave van de vorm (a,h). Dat komt omdat de functie in a en h is geschreven.
a = -0,05, b = 1,2, c = 2
Atop = -b/2a
= -1,2/-0,1 = 12 (normaal Xtop)
htop = h(12) = -0,05 ⋅ (12)2 + 1,2 ⋅ 12 + 2
= -0,05 ⋅ 144 + 14,4 + 2
= -7,2 + 16,4
= 9,2
Dus de top is (12 ; 9,2).
b.
Het is een bergparabool met a < 0.
De maximale hoogte is dus 9,2 meter.
c.
h(26) = -0,05 ⋅ (26)2 + 1,2 ⋅ 26 + 2
= -0,05 ⋅ 676 + 31,2 + 2
= -33,8 + 33,2
= -0,6
Dus bij a = 26 is de hoogte negatief.
Dus de speer raakt de grond al eerder.
Dus Anne gooit de speer minder dan 26 meter.
23.
Tip:
6 uur in de ochtend: t = 6
6 uur in de avond: t = 18
a.6 uur in de ochtend: t = 6
6 uur in de avond: t = 18
t = 6 invullen, levert:
T = -0,05 ⋅ (6)2 + 1,5 ⋅ 6
T = -0,05 ⋅ 36 + 9
T = -1,8 + 9
T = 7,2
Dus bij t = 6 (om 06:00) is de temperatuur 7,2º.
t = 18 invullen, levert:
T = -0,05 ⋅ (18)2 + 1,5 ⋅ 18
T = -0,05 ⋅ 324 + 27
T = -16,2 + 27
T = 10,8
Dus bij t = 18 (om 18:00) is de temperatuur 10,8º.
b.
Bereken dus de Xtop of in dit geval de ttop.
a = -0,05, b = 1,5, c = 0
Xtop = ttop = -b/2a = -1,5/-0,1 = 15
Dus bij t = 15 (om 15:00) is de temperatuur maximaal.
c.
Maximale temperatuur = Ytop = Ttop =
T(15) = -0,05 ⋅ (15)2 + 1,5 ⋅ 15
= -0,05 ⋅ 225 + 22,5
= -11,25 + 22,5
= 11,25
Dus om 15:00 is de maximale temperatuur gelijk aan 11,25º.
Andere paragrafen:
3.1. Kwadratische formules (1 t/m 16)
3.2. De top van een parabool (17 t/m 23)
3.3. Kwadratische functies (24 t/m 35)
3.4. Ontbinden in factoren (36 t/m 50)
3.5. Toepassingen van kwadratische vergelijkingen (51 t/m 62)
3.1. Kwadratische formules (1 t/m 16)
3.2. De top van een parabool (17 t/m 23)
3.3. Kwadratische functies (24 t/m 35)
3.4. Ontbinden in factoren (36 t/m 50)
3.5. Toepassingen van kwadratische vergelijkingen (51 t/m 62)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


