TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.3 Snijpunten van grafieken VWO 3
Boek: Getal & Ruimte - Kwadratische problemen VWO 3 (deel 1) opgaven 27 t/m 35, 2011- Snijpunten van een grafiek f(x) met de x-as: dan is de y-coördinaat gelijk aan 0.
Voorbeelden (3,0) en (-2,0). Je ziet dat y = 0 => dus los op f(x) = 0.
- Snijpunt van een grafiek f(x) met de y-as: dan is de x-coördinaat gelijk aan 0.
Voorbeelden (0,4) en (0,-3). Je ziet dat x = 0 => dus bereken f(0).
- Snijpunten van 2 grafieken f(x) en g(x): waar zijn de 2 grafieken aan elkaar gelijk?
Dus los op de vergelijking f(x) = g(x).
Voorbeelden (3,0) en (-2,0). Je ziet dat y = 0 => dus los op f(x) = 0.
- Snijpunt van een grafiek f(x) met de y-as: dan is de x-coördinaat gelijk aan 0.
Voorbeelden (0,4) en (0,-3). Je ziet dat x = 0 => dus bereken f(0).
- Snijpunten van 2 grafieken f(x) en g(x): waar zijn de 2 grafieken aan elkaar gelijk?
Dus los op de vergelijking f(x) = g(x).
27.
Voorbeelden van punten op de x-as: (1,0) en (3,0) en (12,0) en (-8,0) en (110,0).
Dus je ziet dat de y-coördinaat dan steeds 0 is.
Voorbeelden van punten op de y-as: (0,1) en (0,-19) en (0,7) en (0,87) en (0,-14).
Dus je ziet dat de x-coördinaat dan steeds 0 is.
b.
f(0) = (0)2 + 2 ⋅ 0 - 8 = 0 + 0 - 8 = -8
Dus snijpunt met de y-as: (0,-8).
c.
f(2) = (2)2 + 2 ⋅ 2 - 8 = 4 + 4 - 8 = 8 - 8 = 0
Dus je hebt het punt (2,0) te pakken. En dat punt is punt B in het plaatje.
d.
f(-4) = (-4)2 + 2 ⋅ -4 - 8 = 16 - 8 - 8 = 16 - 16 = 0
Dus je hebt het punt (-4,0) te pakken. En dat punt is punt A in het plaatje.
e.
Los op: x2 + 2x - 8 = 0
28.
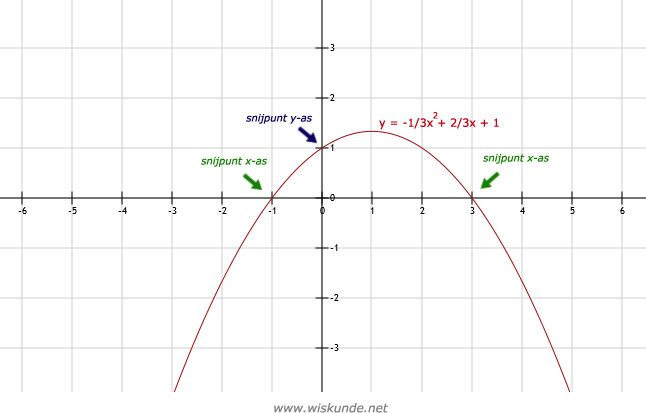
-1/3x2 + 2/3x + 1 = 0 (breuken wegwerken links en rechts maal -3)
x2 - 2x - 3 = 0 (product-som-methode met -3)
(x + 1)(x - 3) = 0
x + 1 = 0 v x - 3 = 0
x = -1 v x = 3
Dus de snijpunten met de x-as zijn (y=0): (-1,0) en (3,0).
Snijpunt met de y-as: x = 0 ofwel bereken g(0):
g(0) = -1/3 ⋅ (0)2 + 2/3 ⋅ 0 + 1
= 0 + 0 + 1
= 1
Dus snijpunt met de y-as (x=0): (0,1).
29.
-1/2x2 - 5x = 0 (links en rechts maal -2)
x2 + 10x = 0 (haal x voor de haakjes)
x(x + 10) = 0
x = 0 v x + 10 = 0
x = 0 v x = -10
Dus de snijpunten met de x-as zijn (y=0): (0,0) en (-10,0).
Snijpunt met de y-as: x = 0 ofwel bereken h(0):
h(0) = -1/2 ⋅ (0)2 - 5 ⋅ 0
= 0 - 0
= 0
Dus snijpunt met de y-as (x=0): (0,0).
30.
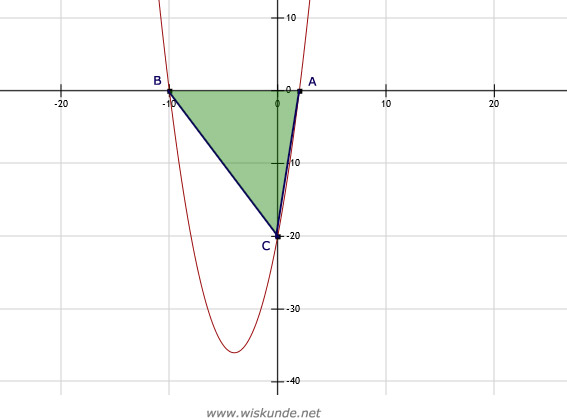
x2 + 8x - 20 = 0 (product-som-methode met -20)
(x - 2)(x + 10) = 0
x - 2 = 0 v x + 10 = 0
x = 2 v x = -10
Dus de snijpunten met de x-as zijn (y=0): A(2,0) en B(-10,0).
Snijpunt met de y-as: x = 0 ofwel bereken f(0):
f(0) = 02 + 8 ⋅ 0 - 20 = -20
Dus snijpunt met de y-as is (0,-20).
Oppervlakte driehoek = 1/2 x basis x hoogte
= 1/2 x AB x OC
= 1/2 x 12 x 20
= 120
31.
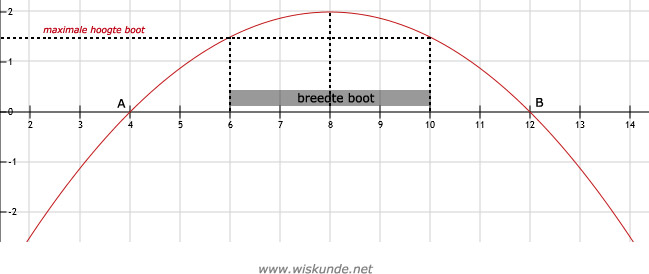
Snijpunten met de x-as: y = 0
Dus: -0,125x2 + 2x - 6 = 0 (links en rechts :-0,125)
x2 - 16x + 48 = 0 (product-som-methode met +48)
(x - 4)(x - 12) = 0
x - 4 = 0 v x - 12 = 0
x = 4 v x = 12
Dus A(4,0) en B(12,0). Zie afbeelding.
b.
De Xtop van de parabool zit in het midden tussen 4 en 12. Dus Xtop = 8.
De boot ligt dan bij x = 6 en x = 10 (beide kanten 2 meter erbij bij x = 8).
Bereken dus de hoogte bij x = 6 en x = 10.
y = -0,125 ⋅ (6)2 + 2 ⋅ 6 - 6
y = -4,5 + 12 - 6
y = 1,5
Dus de hoogte bij x = 6 (en x = 10 op basis van symmetrie) is 1,5 meter.
Dus de boot van 1,40 meter kan er onder door.
32.
x2 - 3x - 1 = -2x + 5 (links en rechts +2x)
x2 - x - 1 = 5 (links en rechts -5)
x2 - x - 6 = 0 (product-som-methode met -6)
(x + 2)(x - 3) = 0
x + 2 = 0 v x - 3 = 0
x = -2 v x = 3
Om de y-waarden van de snijpunten te berekenen, vul x = -2 in de rechte lijn g(x). Deze is makkelijker.
g(-2) = -2 ⋅ -2 + 5 = 4 + 5 = 9. Dus A(-2,9).
g(3) = -2 ⋅ 3 + 5 = -6 + 5 = -1. Dus B(3,-1).
De snijpunten zijn dus A(-2,9) en B(3,-1).
33.
f(x) = g(x)
-x2 + 4x = -2x + 5
-x2 + 6x - 5 = 0
x2 - 6x + 5 = 0
(x - 1)(x - 5) = 0
x - 1 = 0 x - 5 = 0
x = 1 v x = 5
g(1) = -2 ⋅ 1 + 5 = 3. Dus P(1,3).
g(5) = -2 ⋅ 5 + 5 = -5. Dus Q(5,-5).
b.
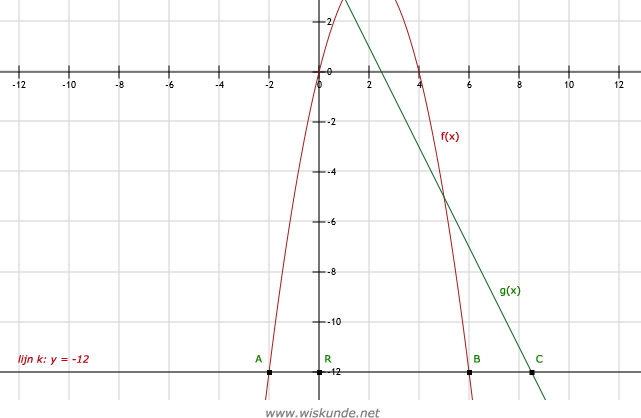
Afstand AB -> bereken f(x) = -12
-x2 + 4x = -12
-x2 + 4x + 12 = 0
x2 - 4x - 12 = 0 (product-som-methode met -12)
(x + 2)(x - 6) = 0
x + 2 = 0 x - 6 = 0
x = -2 v x = 6
Dus A(-2,-12) en B(6,-12). Dus de afstand tussen A en B is het verschil tussen de x-waarden: XB - XA = 8.
Dus AB = 8.
BC ->
Bereken eerst punt C:
g(x) = -12
-2x + 5 = -12
-2x = -17
x = -17/-2 = 8½
Dus punt C is C(8½ ; -12).
Afstand BC => XC - XB = 8½ - 6 = 2½
Dus BC = 2½
34.
-x2 - 18x - 86 = -2x - 58
-x2 - 16x - 28 = 0
x2 + 16x + 28 = 0 (product-som-methode met +28)
(x + 2)(x + 14) = 0
x + 2 = 0 v x + 14 = 0
x = -2 v x = -14
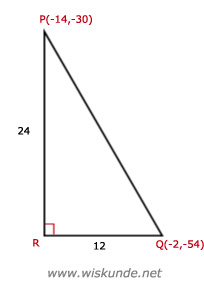
g(-2) = -2 ⋅ -2 - 58 = -54. Dus Q(-2,-54).
g(-14) = -2 ⋅ -14 - 58 = -30. Dus P(-14,-30).
PQ2 = QR2 + PR2
PQ2 = 122 + 242
PQ2 = 720
PQ = √720
PQ ≈ 26,83
Dus oppervlakte rooster = 26,83 x 60 ≈ 1609,8 cm2.
Afgerond op gehelen: 1610 cm2
35.
De punten O en Q zijn de snijpunten van de parabool met de x-as. Dus los op: f(x) = 0
-0,0075x2 + 1,5x = 0 (links en rechts :-0,0075)
x2 - 200x = 0 (x voor de haakjes halen)
x(x - 200) = 0
x = 0 v x = 200
Dus snijpunten x-as: O(0,0) en Q(200,0).
De afstand tussen O en Q is dus 200 meter.
b.
Bereken de Xtop en Ytop.
Xtop = -b/2a = -1,5 / (2 ⋅ -0,0075) = 100
Ytop = -0,0075 ⋅ (100)2 + 1,5 ⋅ 100 = 75
Dus top is (100,75).
Dus de maximale hoogte is 75 meter.
c.
f(x) = g(x) levert:
(x - 20)(x - 160) = 0
x = 20 v x = 160
x = 20 geeft y = 27, dus A(20,27).
x = 160 geeft y = 48, dus B(160,48).
Met Pythagoras: AB = √20041 ≈ 141,6 meter
Tip:
Snijpunt met de x-as: y = 0
Snijpunt met de y-as: x = 0
a. Snijpunt met de x-as: y = 0
Snijpunt met de y-as: x = 0
Voorbeelden van punten op de x-as: (1,0) en (3,0) en (12,0) en (-8,0) en (110,0).
Dus je ziet dat de y-coördinaat dan steeds 0 is.
Voorbeelden van punten op de y-as: (0,1) en (0,-19) en (0,7) en (0,87) en (0,-14).
Dus je ziet dat de x-coördinaat dan steeds 0 is.
b.
f(0) = (0)2 + 2 ⋅ 0 - 8 = 0 + 0 - 8 = -8
Dus snijpunt met de y-as: (0,-8).
c.
f(2) = (2)2 + 2 ⋅ 2 - 8 = 4 + 4 - 8 = 8 - 8 = 0
Dus je hebt het punt (2,0) te pakken. En dat punt is punt B in het plaatje.
d.
f(-4) = (-4)2 + 2 ⋅ -4 - 8 = 16 - 8 - 8 = 16 - 16 = 0
Dus je hebt het punt (-4,0) te pakken. En dat punt is punt A in het plaatje.
e.
Los op: x2 + 2x - 8 = 0
28.
Tip:
Snijpunt met de y-as is altijd makkelijker. Want x = 0 invullen is vaak heel eenvoudig.
Snijpunten met de x-as: y = 0 ofwel g(x) = 0:Snijpunt met de y-as is altijd makkelijker. Want x = 0 invullen is vaak heel eenvoudig.
-1/3x2 + 2/3x + 1 = 0 (breuken wegwerken links en rechts maal -3)
x2 - 2x - 3 = 0 (product-som-methode met -3)
(x + 1)(x - 3) = 0
x + 1 = 0 v x - 3 = 0
x = -1 v x = 3
Dus de snijpunten met de x-as zijn (y=0): (-1,0) en (3,0).
Snijpunt met de y-as: x = 0 ofwel bereken g(0):
g(0) = -1/3 ⋅ (0)2 + 2/3 ⋅ 0 + 1
= 0 + 0 + 1
= 1
Dus snijpunt met de y-as (x=0): (0,1).

29.
Tip:
Snijpunt met de y-as dan geldt: x = 0. Dus vul x = 0 in de functie van h(x). Dat levert dus h(0) = 0.
Snijpunten met de x-as: y = 0 ofwel h(x) = 0:Snijpunt met de y-as dan geldt: x = 0. Dus vul x = 0 in de functie van h(x). Dat levert dus h(0) = 0.
-1/2x2 - 5x = 0 (links en rechts maal -2)
x2 + 10x = 0 (haal x voor de haakjes)
x(x + 10) = 0
x = 0 v x + 10 = 0
x = 0 v x = -10
Dus de snijpunten met de x-as zijn (y=0): (0,0) en (-10,0).
Snijpunt met de y-as: x = 0 ofwel bereken h(0):
h(0) = -1/2 ⋅ (0)2 - 5 ⋅ 0
= 0 - 0
= 0
Dus snijpunt met de y-as (x=0): (0,0).
30.
Tip:
oppervlakte driehoek = 1/2 x basis x hoogte
lengte AB: tussen x = -10 en x = 2 zit 12 cm
Snijpunten met de x-as: y = 0 ofwel f(x) = 0:oppervlakte driehoek = 1/2 x basis x hoogte
lengte AB: tussen x = -10 en x = 2 zit 12 cm
x2 + 8x - 20 = 0 (product-som-methode met -20)
(x - 2)(x + 10) = 0
x - 2 = 0 v x + 10 = 0
x = 2 v x = -10
Dus de snijpunten met de x-as zijn (y=0): A(2,0) en B(-10,0).
Snijpunt met de y-as: x = 0 ofwel bereken f(0):
f(0) = 02 + 8 ⋅ 0 - 20 = -20
Dus snijpunt met de y-as is (0,-20).
Oppervlakte driehoek = 1/2 x basis x hoogte
= 1/2 x AB x OC
= 1/2 x 12 x 20
= 120

31.
Tip:
Het midden van de boot ligt bij de Xtop. De boot ligt in het midden.
Y6 en Y10 vormen de maximale hoogte van de boot.
Y6 is de y-waarde bij x = 6.
a.Het midden van de boot ligt bij de Xtop. De boot ligt in het midden.
Y6 en Y10 vormen de maximale hoogte van de boot.
Y6 is de y-waarde bij x = 6.
Snijpunten met de x-as: y = 0
Dus: -0,125x2 + 2x - 6 = 0 (links en rechts :-0,125)
x2 - 16x + 48 = 0 (product-som-methode met +48)
(x - 4)(x - 12) = 0
x - 4 = 0 v x - 12 = 0
x = 4 v x = 12
Dus A(4,0) en B(12,0). Zie afbeelding.
b.
De Xtop van de parabool zit in het midden tussen 4 en 12. Dus Xtop = 8.
De boot ligt dan bij x = 6 en x = 10 (beide kanten 2 meter erbij bij x = 8).
Bereken dus de hoogte bij x = 6 en x = 10.
y = -0,125 ⋅ (6)2 + 2 ⋅ 6 - 6
y = -4,5 + 12 - 6
y = 1,5
Dus de hoogte bij x = 6 (en x = 10 op basis van symmetrie) is 1,5 meter.
Dus de boot van 1,40 meter kan er onder door.

32.
Tip:
Snijpunten van 2 grafieken: los op f(x) = g(x).
Dus waar zijn de grafieken gelijk aan elkaar? Dat is natuurlijk bij de snijpunten.
Los op: f(x) = g(x)Snijpunten van 2 grafieken: los op f(x) = g(x).
Dus waar zijn de grafieken gelijk aan elkaar? Dat is natuurlijk bij de snijpunten.
x2 - 3x - 1 = -2x + 5 (links en rechts +2x)
x2 - x - 1 = 5 (links en rechts -5)
x2 - x - 6 = 0 (product-som-methode met -6)
(x + 2)(x - 3) = 0
x + 2 = 0 v x - 3 = 0
x = -2 v x = 3
Om de y-waarden van de snijpunten te berekenen, vul x = -2 in de rechte lijn g(x). Deze is makkelijker.
g(-2) = -2 ⋅ -2 + 5 = 4 + 5 = 9. Dus A(-2,9).
g(3) = -2 ⋅ 3 + 5 = -6 + 5 = -1. Dus B(3,-1).
De snijpunten zijn dus A(-2,9) en B(3,-1).
33.
Tip:
Als je P en Q gevonden hebt, controleer dan dat elk punt op zowel f(x) als g(x) ligt door het in te vullen.
Bij b: maak een schets! Bedenk dat het een bergparabool is.
a.Als je P en Q gevonden hebt, controleer dan dat elk punt op zowel f(x) als g(x) ligt door het in te vullen.
Bij b: maak een schets! Bedenk dat het een bergparabool is.
f(x) = g(x)
-x2 + 4x = -2x + 5
-x2 + 6x - 5 = 0
x2 - 6x + 5 = 0
(x - 1)(x - 5) = 0
x - 1 = 0 x - 5 = 0
x = 1 v x = 5
g(1) = -2 ⋅ 1 + 5 = 3. Dus P(1,3).
g(5) = -2 ⋅ 5 + 5 = -5. Dus Q(5,-5).
b.
Afstand AB -> bereken f(x) = -12
-x2 + 4x = -12
-x2 + 4x + 12 = 0
x2 - 4x - 12 = 0 (product-som-methode met -12)
(x + 2)(x - 6) = 0
x + 2 = 0 x - 6 = 0
x = -2 v x = 6
Dus A(-2,-12) en B(6,-12). Dus de afstand tussen A en B is het verschil tussen de x-waarden: XB - XA = 8.
Dus AB = 8.
BC ->
Bereken eerst punt C:
g(x) = -12
-2x + 5 = -12
-2x = -17
x = -17/-2 = 8½
Dus punt C is C(8½ ; -12).
Afstand BC => XC - XB = 8½ - 6 = 2½
Dus BC = 2½

34.
Tip:
Bepaal eerst de coördinaten van P en Q door f(x) = g(x) op te lossen.
Bereken daarna PQ met de Stelling van Pythagoras.
Los op: f(x) = g(x)Bepaal eerst de coördinaten van P en Q door f(x) = g(x) op te lossen.
Bereken daarna PQ met de Stelling van Pythagoras.
-x2 - 18x - 86 = -2x - 58
-x2 - 16x - 28 = 0
x2 + 16x + 28 = 0 (product-som-methode met +28)
(x + 2)(x + 14) = 0
x + 2 = 0 v x + 14 = 0
x = -2 v x = -14
g(-2) = -2 ⋅ -2 - 58 = -54. Dus Q(-2,-54).
g(-14) = -2 ⋅ -14 - 58 = -30. Dus P(-14,-30).
PQ2 = QR2 + PR2
PQ2 = 122 + 242
PQ2 = 720
PQ = √720
PQ ≈ 26,83
Dus oppervlakte rooster = 26,83 x 60 ≈ 1609,8 cm2.
Afgerond op gehelen: 1610 cm2

35.
Tip:
Je ziet al meteen welke formule de parabool is en welke de rechte lijn.
Neem als f(x) de parabool en als g(x) de rechte lijn en los op: f(x) = g(x) voor de punten A en B.
a.Je ziet al meteen welke formule de parabool is en welke de rechte lijn.
Neem als f(x) de parabool en als g(x) de rechte lijn en los op: f(x) = g(x) voor de punten A en B.
De punten O en Q zijn de snijpunten van de parabool met de x-as. Dus los op: f(x) = 0
-0,0075x2 + 1,5x = 0 (links en rechts :-0,0075)
x2 - 200x = 0 (x voor de haakjes halen)
x(x - 200) = 0
x = 0 v x = 200
Dus snijpunten x-as: O(0,0) en Q(200,0).
De afstand tussen O en Q is dus 200 meter.
b.
Bereken de Xtop en Ytop.
Xtop = -b/2a = -1,5 / (2 ⋅ -0,0075) = 100
Ytop = -0,0075 ⋅ (100)2 + 1,5 ⋅ 100 = 75
Dus top is (100,75).
Dus de maximale hoogte is 75 meter.
c.
f(x) = g(x) levert:
(x - 20)(x - 160) = 0
x = 20 v x = 160
x = 20 geeft y = 27, dus A(20,27).
x = 160 geeft y = 48, dus B(160,48).
Met Pythagoras: AB = √20041 ≈ 141,6 meter
Andere paragrafen:
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


