TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.1 Kwadratische functies VWO 3
Boek: Getal & Ruimte - Kwadratische problemen VWO 3 (deel 1) opgaven 1 t/m 12, 2011Een kwadratische formule is een formule van de 2e macht. Er zit dus altijd een kwadraat in.
De basisformule is: y = ax2 + bx + c, met a ≠ 0 want anders hebben we te maken met een rechte lijn.
Als a > 0 dan is het een dalparabool
Als a < 0 dan is het een bergparabool
Van een parabool kunnen we de top bepalen en eventueel de snijpunten met de x-as en y-as.
Voorbeelden van een kwadratische formule: y = x2 of y = -0.5x2 + 6x -3
De basisformule is: y = ax2 + bx + c, met a ≠ 0 want anders hebben we te maken met een rechte lijn.
Als a > 0 dan is het een dalparabool
Als a < 0 dan is het een bergparabool
Van een parabool kunnen we de top bepalen en eventueel de snijpunten met de x-as en y-as.
Voorbeelden van een kwadratische formule: y = x2 of y = -0.5x2 + 6x -3
1.
f(3) = 3 ⋅ (3)2 + 8 = 3 ⋅ 9 + 8 = 27 + 8 = 35
b.
f(-8) = 3 ⋅ (-8)2 + 8 = 3 ⋅ 64 + 8 = 192 + 8 = 200
f(0) = 3 ⋅ (0)2 + 8 = 3 ⋅ 0 + 8 = 0 + 8 = 8
f(1) = 3 ⋅ (1)2 + 8 = 3 ⋅ 1 + 8 = 3 + 8 = 11
2.
g(5) = -2 ⋅ (5)2 + 8 ⋅ 5 = -2 ⋅ 25 + 40 = -50 + 40 = -10
g(-3) = -2 ⋅ (-3)2 + 8 ⋅ -3 = -2 ⋅ 9 - 24 = -18 - 24 = -42
b.
g(-1) = -2 ⋅ (-1)2 + 8 ⋅ -1 = -2 ⋅ 1 - 8 = -2 - 8 = -10
Dus het punt P(-1,-10) ligt op de grafiek.
3.
formule: y = x2 - 7x - 5
b.
h(5) = (5)2 - 7 ⋅ 5 - 5 = 25 - 35 - 5 = -15
h(-4) = (-4)2 - 7 ⋅ -4 - 5 = 16 + 28 - 5 = 39
c.
A(-1,y), dus YA => h(-1) = (-1)2 - 7 ⋅ -1 - 5 = 1 + 7 - 5 = 3
Dus we hebben dan het punt A(-1,3).
d.
B(6,y), dus YB => h(6) = (6)2 - 7 ⋅ 6 - 5 = 36 - 42 - 5 = -11
Dus we hebben dan het punt B(6,-11).
4.
a. f(-1) = (-1)2 - 4 ⋅ -1 + 3 = 1 + 4 + 3 = 8
b.
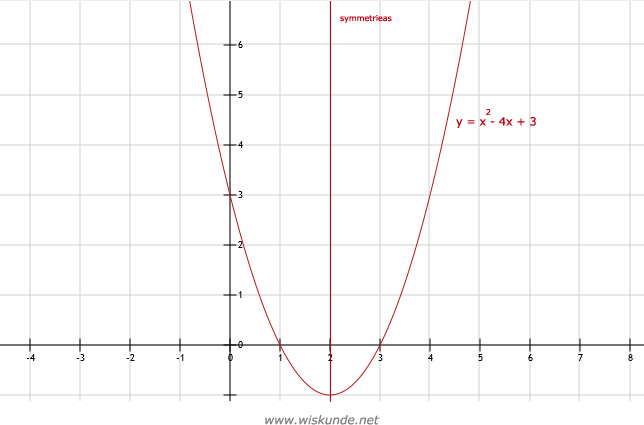
c. De volgende punten liggen op de grafiek: (-1,8) en (0,3) en (1,0) en (2,-1) enz.
d. Zie afbeelding
e. Het laagste punt is de top: (2,-1).
5.
g(-2) = -(-2)2 + 2 ⋅ -2 + 7 = -4 - 4 + 7 = -8 + 7 = -1
g(4) = -(4)2 + 2 ⋅ 4 + 7 = -16 + 8 + 7 = -16 + 15 = -1
b.
g(-1) = -(-1)2 + 2 ⋅ -1 + 7 = -1 - 2 + 7 = -3 + 7 = 4
Op basis van symmetrie weet je nu ook dat g(3) = 4.
c.
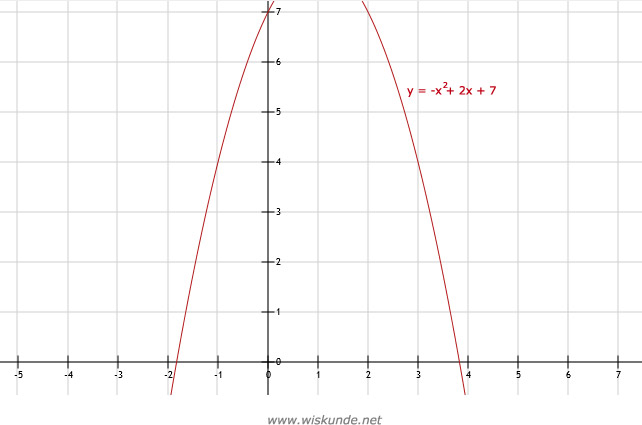
d. Zie afbeelding
e. Het hoogste punt is de top. De top is (1,8).
6.
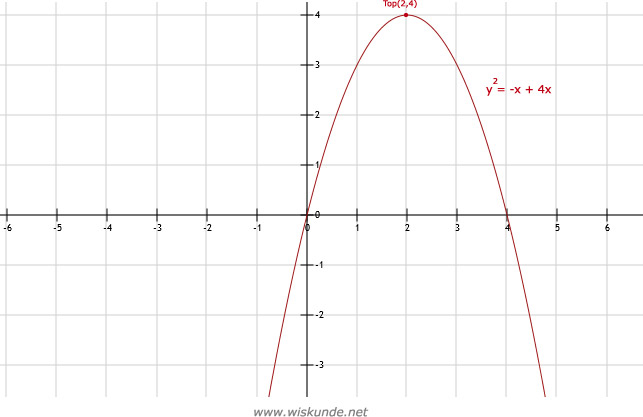
b. Coördinaten van de top zijn: Top(2,4).
7.
b.
g(10) = 1/2 ⋅ (10)2 - 2 ⋅ 10 + 1
= 1/2 ⋅ 100 - 20 + 1
= 50 - 20 + 1
= 31
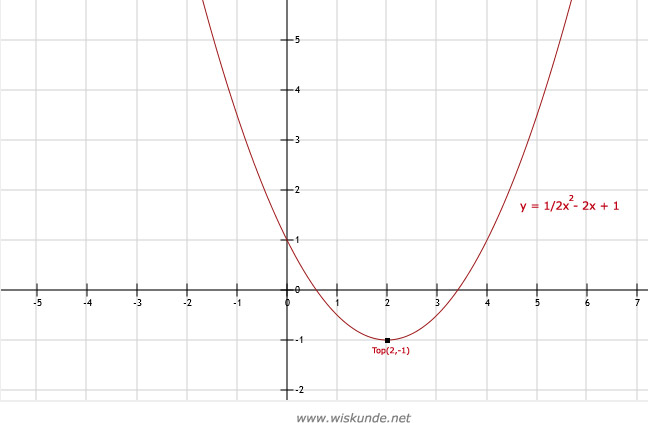
Ja, het punt (10,31) ligt dus op de grafiek.
8.
Punten op de lijn:
Punten op de parabool:
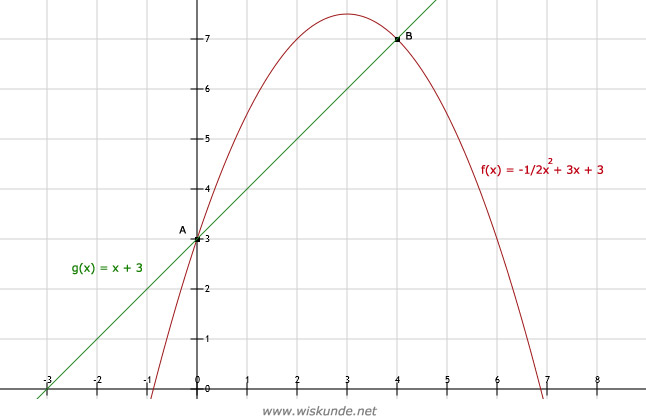
b. Lees de punten af in de grafiek: A(0,3) en B(4,7).
c.
Vul x = -4 in f(x) en g(x) en trek de y-waarden van elkaar af.
f(-4) = -1/2 ⋅ (-4)2 + 3 ⋅ -4 + 3 = -1/2 ⋅ 16 - 12 + 3 = -8 - 12 + 3 = -17
Dus de lijn l: en de grafiek f snijden in Q(-4,-17).
g(-4) = -4 + 3 = -1
Dus de lijn l: en de grafiek g snijden in R(-4,-1).
Dus de lengte van lijnstuk QR is het verschil in de y-waarden. Tussen -17 en -1 ligt 16 cm. Dus QR = 16 cm.
9.
x = 4 invullen, levert: h = -0,06 ⋅ (4)2 + 0,72 ⋅ 4 + 2,1 = -0,06 ⋅ 16 + 2,88 + 2,1 = -0,96 + 4,98 = 4,02
Dus bij x = 4 is de hoogte van de shuttle 4,02 meter.
b.
x = 2 invullen, levert: h = -0,06 ⋅ (2)2 + 0,72 ⋅ 2 + 2,1 = -0,06 ⋅ 4 + 1,44 + 2,1 = -0,24 + 3,54 = 3,3
x = 10 invullen, levert: h = -0,06 ⋅ (10)2 + 0,72 ⋅ 10 + 2,1 = -0,06 ⋅ 100 + 7,2 + 2,1 = -6 + 9,3 = 3,3
Dus je ziet dat bij x = 2 en x = 10 de hoogte gelijk is.
c.
De Xtop ligt op basis van symmetrie in het midden van x = 2 en x = 10. Dat is dus bij x = 6.
x = 6 invullen, levert: h = -0,06 ⋅ (6)2 + 0,72 ⋅ 6 + 2,1 = -0,06 ⋅ 36 + 4,32 + 2,1 = -2,16 + 6,42 = 4,26
Dus de top is bij (6 ; 4,26).
d.
x = 14 invullen, levert: h = -0,06 ⋅ (14)2 + 0,72 ⋅ 14 + 2,1 = -0,06 ⋅ 196 + 10,08 + 2,1 = -11,76 + 12,18 = 0,42
Dus bij x = 14 is de hoogte 0,42 meter.
Dus de shuttle is dan nog niet op de grond.
10.
Vul in x = 1 in h: levert:
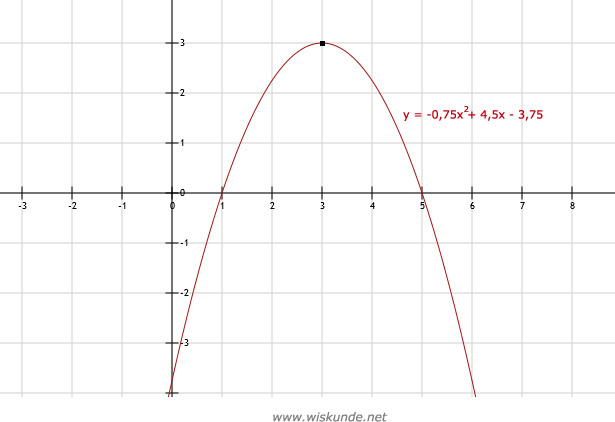
h(1) = -0,75 ⋅ (1)2 + 4,5 ⋅ 1 - 3,75 = -0,75 + 4,5 - 3,75 = 3,75 - 3,75 = 0
Vul in x = 5 in h: levert:
h(5) = -0,75 ⋅ (5)2 + 4,5 ⋅ 5 - 3,75 = -0,75 ⋅ 25 + 22,5 - 3,75 = -18,75 + 22,5 - 3,75 = 3,75 - 3,75 = 0
Dus bij x = 1 en x = 5 is de hoogte gelijk aan 0 (snijpunten parabool met de x-as).
b.
De Xtop ligt in het midden tussen x = 1 en x = 5. Dus Xtop = 3.
Vul in x = 3 in h: levert:
h(3) = -0,75 ⋅ (3)2 + 4,5 ⋅ 3 - 3,75 = -0,75 ⋅ 9 + 13,5 - 3,75 = -6,75 + 9,75 = 3
Dus maximale hoogte is 3 meter. Dus top van de parabool is: Top(3,3)
c.
Als de bestelbus een breedte heeft van 2 meter en deze rijdt in het midden van de tunnel dan hebben we te maken met x = 2 en x = 4.
Vul in x = 2 in h: levert:
h(2) = -0,75 ⋅ (2)2 + 4,5 ⋅ 2 - 3,75 = -0,75 ⋅ 4 + 9 - 3,75 = -3 + 9 - 3,75 = 2,25
Op basis van symmetrie is h(4) dan ook gelijk aan 2,25.
Dus de hoogte die erbij hoort is 2,25.
Dus de bestelbus past net. De bus heeft 5 cm over.
Tip:
f(3) wil zeggen; vul x = 3 in de functie. De uitkomst is het beeld van de functie.
a.f(3) wil zeggen; vul x = 3 in de functie. De uitkomst is het beeld van de functie.
f(3) = 3 ⋅ (3)2 + 8 = 3 ⋅ 9 + 8 = 27 + 8 = 35
b.
f(-8) = 3 ⋅ (-8)2 + 8 = 3 ⋅ 64 + 8 = 192 + 8 = 200
f(0) = 3 ⋅ (0)2 + 8 = 3 ⋅ 0 + 8 = 0 + 8 = 8
f(1) = 3 ⋅ (1)2 + 8 = 3 ⋅ 1 + 8 = 3 + 8 = 11
2.
Tip:
Denk aan de haakjes!
(-2)2 = -2 x -2 = 4
Maar -22 = - 2 x 2 = -4
a.Denk aan de haakjes!
(-2)2 = -2 x -2 = 4
Maar -22 = - 2 x 2 = -4
g(5) = -2 ⋅ (5)2 + 8 ⋅ 5 = -2 ⋅ 25 + 40 = -50 + 40 = -10
g(-3) = -2 ⋅ (-3)2 + 8 ⋅ -3 = -2 ⋅ 9 - 24 = -18 - 24 = -42
b.
g(-1) = -2 ⋅ (-1)2 + 8 ⋅ -1 = -2 ⋅ 1 - 8 = -2 - 8 = -10
Dus het punt P(-1,-10) ligt op de grafiek.
3.
Tip:
Je kunt een grafiek dus opschrijven met een formule of met haakjes notatie.
a.Je kunt een grafiek dus opschrijven met een formule of met haakjes notatie.
formule: y = x2 - 7x - 5
b.
h(5) = (5)2 - 7 ⋅ 5 - 5 = 25 - 35 - 5 = -15
h(-4) = (-4)2 - 7 ⋅ -4 - 5 = 16 + 28 - 5 = 39
c.
A(-1,y), dus YA => h(-1) = (-1)2 - 7 ⋅ -1 - 5 = 1 + 7 - 5 = 3
Dus we hebben dan het punt A(-1,3).
d.
B(6,y), dus YB => h(6) = (6)2 - 7 ⋅ 6 - 5 = 36 - 42 - 5 = -11
Dus we hebben dan het punt B(6,-11).
4.
a. f(-1) = (-1)2 - 4 ⋅ -1 + 3 = 1 + 4 + 3 = 8
b.
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | 8 | 3 | 0 | -1 | 0 | 3 | 8 |
d. Zie afbeelding
e. Het laagste punt is de top: (2,-1).

5.
Tip:
In de tabel zie je dat de top is op basis van symmetrie: (1,8).
a.In de tabel zie je dat de top is op basis van symmetrie: (1,8).
g(-2) = -(-2)2 + 2 ⋅ -2 + 7 = -4 - 4 + 7 = -8 + 7 = -1
g(4) = -(4)2 + 2 ⋅ 4 + 7 = -16 + 8 + 7 = -16 + 15 = -1
b.
g(-1) = -(-1)2 + 2 ⋅ -1 + 7 = -1 - 2 + 7 = -3 + 7 = 4
Op basis van symmetrie weet je nu ook dat g(3) = 4.
c.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -1 | 4 | 7 | 8 | 7 | 4 | -1 |
e. Het hoogste punt is de top. De top is (1,8).

6.
Tip:
In de tabel bij a. zie je op basis van symmetrie de top bij x = 2. De bijbehorende y = 4. Dus de top is (2,4).
Je ziet in de tabel ook de snijpunten met de x-as. Want bij een snijpunt met de x-as geldt y = 0. Dat is dus bij x = 0 en x = 4. Dus de snijpunten met de x-as zijn: (0,0) en (4,0). Ook zie je dit in de getekende grafiek.
a.In de tabel bij a. zie je op basis van symmetrie de top bij x = 2. De bijbehorende y = 4. Dus de top is (2,4).
Je ziet in de tabel ook de snijpunten met de x-as. Want bij een snijpunt met de x-as geldt y = 0. Dat is dus bij x = 0 en x = 4. Dus de snijpunten met de x-as zijn: (0,0) en (4,0). Ook zie je dit in de getekende grafiek.
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | -5 | 0 | 3 | 4 | 3 | 0 | -5 |

7.
Tip:
Wil punt A(10,31) op de grafiek liggen dan moet het punt een oplossing zijn voor de formule: y = 1/2x2 - 2x + 1.
Dus vul x = 10 in de formule en kijk of y dan gelijk is aan 31. Klopt dit dan ligt het getallenpaar op de grafiek.
a.Wil punt A(10,31) op de grafiek liggen dan moet het punt een oplossing zijn voor de formule: y = 1/2x2 - 2x + 1.
Dus vul x = 10 in de formule en kijk of y dan gelijk is aan 31. Klopt dit dan ligt het getallenpaar op de grafiek.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 7 | 3,5 | 1 | -0,5 | -1 | -0,5 | 1 | 3,5 | 7 |
g(10) = 1/2 ⋅ (10)2 - 2 ⋅ 10 + 1
= 1/2 ⋅ 100 - 20 + 1
= 50 - 20 + 1
= 31
Ja, het punt (10,31) ligt dus op de grafiek.

8.
Tip:
Om een lijn te tekenen, hoef je maar 2 punten te weten.
Om een parabool te tekenen, moet je 7 punten weten.
De lijn x = -4 is een verticale lijn door bijvoorbeeld de punten (-4,1) en (-4,-5) en (-4,8) enz.
a.Om een lijn te tekenen, hoef je maar 2 punten te weten.
Om een parabool te tekenen, moet je 7 punten weten.
De lijn x = -4 is een verticale lijn door bijvoorbeeld de punten (-4,1) en (-4,-5) en (-4,8) enz.
Punten op de lijn:
| x | 0 | 4 |
| g(x) | 3 | 7 |
Punten op de parabool:
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| f(x) | -0,5 | 3 | 5,5 | 7 | 7,5 | 7 | 5,5 | 3 | -0,5 | -5 |
c.
Vul x = -4 in f(x) en g(x) en trek de y-waarden van elkaar af.
f(-4) = -1/2 ⋅ (-4)2 + 3 ⋅ -4 + 3 = -1/2 ⋅ 16 - 12 + 3 = -8 - 12 + 3 = -17
Dus de lijn l: en de grafiek f snijden in Q(-4,-17).
g(-4) = -4 + 3 = -1
Dus de lijn l: en de grafiek g snijden in R(-4,-1).
Dus de lengte van lijnstuk QR is het verschil in de y-waarden. Tussen -17 en -1 ligt 16 cm. Dus QR = 16 cm.

9.
Tip:
Zie dat de boog die de shuttle maakt, lijkt op een parabool. Waar de parabool de x -as snijdt, daar is de hoogte gelijk aan 0 en ligt dus de shuttle op de grond.
a.Zie dat de boog die de shuttle maakt, lijkt op een parabool. Waar de parabool de x -as snijdt, daar is de hoogte gelijk aan 0 en ligt dus de shuttle op de grond.
x = 4 invullen, levert: h = -0,06 ⋅ (4)2 + 0,72 ⋅ 4 + 2,1 = -0,06 ⋅ 16 + 2,88 + 2,1 = -0,96 + 4,98 = 4,02
Dus bij x = 4 is de hoogte van de shuttle 4,02 meter.
b.
x = 2 invullen, levert: h = -0,06 ⋅ (2)2 + 0,72 ⋅ 2 + 2,1 = -0,06 ⋅ 4 + 1,44 + 2,1 = -0,24 + 3,54 = 3,3
x = 10 invullen, levert: h = -0,06 ⋅ (10)2 + 0,72 ⋅ 10 + 2,1 = -0,06 ⋅ 100 + 7,2 + 2,1 = -6 + 9,3 = 3,3
Dus je ziet dat bij x = 2 en x = 10 de hoogte gelijk is.
c.
De Xtop ligt op basis van symmetrie in het midden van x = 2 en x = 10. Dat is dus bij x = 6.
x = 6 invullen, levert: h = -0,06 ⋅ (6)2 + 0,72 ⋅ 6 + 2,1 = -0,06 ⋅ 36 + 4,32 + 2,1 = -2,16 + 6,42 = 4,26
Dus de top is bij (6 ; 4,26).
d.
x = 14 invullen, levert: h = -0,06 ⋅ (14)2 + 0,72 ⋅ 14 + 2,1 = -0,06 ⋅ 196 + 10,08 + 2,1 = -11,76 + 12,18 = 0,42
Dus bij x = 14 is de hoogte 0,42 meter.
Dus de shuttle is dan nog niet op de grond.
10.
Tip:
Xtop (dat is de x-coördinaat van de top) ligt precies in het midden van de tunnel op de x-as.
Ytop (dat is de y-coördinaat van de top) is de hoogte van de tunnel.
a.Xtop (dat is de x-coördinaat van de top) ligt precies in het midden van de tunnel op de x-as.
Ytop (dat is de y-coördinaat van de top) is de hoogte van de tunnel.
Vul in x = 1 in h: levert:
h(1) = -0,75 ⋅ (1)2 + 4,5 ⋅ 1 - 3,75 = -0,75 + 4,5 - 3,75 = 3,75 - 3,75 = 0
Vul in x = 5 in h: levert:
h(5) = -0,75 ⋅ (5)2 + 4,5 ⋅ 5 - 3,75 = -0,75 ⋅ 25 + 22,5 - 3,75 = -18,75 + 22,5 - 3,75 = 3,75 - 3,75 = 0
Dus bij x = 1 en x = 5 is de hoogte gelijk aan 0 (snijpunten parabool met de x-as).
b.
De Xtop ligt in het midden tussen x = 1 en x = 5. Dus Xtop = 3.
Vul in x = 3 in h: levert:
h(3) = -0,75 ⋅ (3)2 + 4,5 ⋅ 3 - 3,75 = -0,75 ⋅ 9 + 13,5 - 3,75 = -6,75 + 9,75 = 3
Dus maximale hoogte is 3 meter. Dus top van de parabool is: Top(3,3)
c.
Als de bestelbus een breedte heeft van 2 meter en deze rijdt in het midden van de tunnel dan hebben we te maken met x = 2 en x = 4.
Vul in x = 2 in h: levert:
h(2) = -0,75 ⋅ (2)2 + 4,5 ⋅ 2 - 3,75 = -0,75 ⋅ 4 + 9 - 3,75 = -3 + 9 - 3,75 = 2,25
Op basis van symmetrie is h(4) dan ook gelijk aan 2,25.
Dus de hoogte die erbij hoort is 2,25.
Dus de bestelbus past net. De bus heeft 5 cm over.

11.
v = 12 invullen, levert: A = 0,05 ⋅ (12)2 + 0,28 ⋅ 12 = 0,05 ⋅ 144 + 3,36 = 7,2 + 3,36 = 10,56 (meter)
v = 20 invullen, levert: A = 0,05 ⋅ (20)2 + 0,28 ⋅ 20 = 0,05 ⋅ 400 + 5,6 = 20 + 5,6 = 25,6 (meter)
Dus de veilige afstand neemt toe met 25,6 - 10,56 = 15,04 meter.
b.
90 km/uur => 90/3,6 = 25 m/s
v = 25 invullen, levert: A = 0,05 ⋅ (25)2 + 0,28 ⋅ 25 = 0,05 ⋅ 625 + 7 = 31,25 + 7 = 38,25 (meter)
c.
50 km/uur = 13,89 m/s (delen door 3,6)
v = 13,89 invullen, levert: A = 0,05 ⋅ (13,89)2 + 0,28 ⋅ 13,89 = 9,646605 + 3,8892 ≈ 13,54 (meter)
Bij 50 km/uur is de veilige afstand volgens de formule dus 13,54 meter. Maar Arie had 16 meter nodig. Dus hij reed harder dan 50 km/uur.
12.
t = 3 invullen levert:
h(3) = -4,95 ⋅ (3)2 + 108,9 ⋅ 3 + 8000 = 8282,15
Dus de hoogte bij t = 3 is 8282,15 meter.
t = 19 invullen levert:
h(19) = -4,95 ⋅ (19)2 + 108,9 ⋅ 19 + 8000 = 8282,15
Dus de hoogte bij t = 19 is ook 8282,15 meter.
We hebben dus een symmetrie te pakken.
b.
Xtop is het midden tussen x = 3 en x = 19. Dus Xtop = 11.
Ytop wordt dan:
h(11) = -4,95 ⋅ (11)2 + 108,9 ⋅ 11 + 8000 = 8598,95
Dus de maximale hoogte (bij t = 11) is 8598,95 meter.
c.
De parabolische baan begint bij t = 0. De top ligt bij t = 11.
Dus bij t = 22 is de baan weer op z'n einde. Dus de baan duurt 22 seconden.
Tip:
Hoe groter de snelheid (v) hoe langer de veilige afstand moet zijn (A).
Van km/uur naar m/s -> :3,6
Van m/s naar km/uur -> x3,6
a.Hoe groter de snelheid (v) hoe langer de veilige afstand moet zijn (A).
Van km/uur naar m/s -> :3,6
Van m/s naar km/uur -> x3,6
v = 12 invullen, levert: A = 0,05 ⋅ (12)2 + 0,28 ⋅ 12 = 0,05 ⋅ 144 + 3,36 = 7,2 + 3,36 = 10,56 (meter)
v = 20 invullen, levert: A = 0,05 ⋅ (20)2 + 0,28 ⋅ 20 = 0,05 ⋅ 400 + 5,6 = 20 + 5,6 = 25,6 (meter)
Dus de veilige afstand neemt toe met 25,6 - 10,56 = 15,04 meter.
b.
90 km/uur => 90/3,6 = 25 m/s
v = 25 invullen, levert: A = 0,05 ⋅ (25)2 + 0,28 ⋅ 25 = 0,05 ⋅ 625 + 7 = 31,25 + 7 = 38,25 (meter)
c.
50 km/uur = 13,89 m/s (delen door 3,6)
v = 13,89 invullen, levert: A = 0,05 ⋅ (13,89)2 + 0,28 ⋅ 13,89 = 9,646605 + 3,8892 ≈ 13,54 (meter)
Bij 50 km/uur is de veilige afstand volgens de formule dus 13,54 meter. Maar Arie had 16 meter nodig. Dus hij reed harder dan 50 km/uur.
12.
Tip:
Als je bij een parabool 2 x-waarden hebt met gelijke hoogte, dan bevindt de top zich in het midden van deze 2 x-waarden (symmetrie).
a.Als je bij een parabool 2 x-waarden hebt met gelijke hoogte, dan bevindt de top zich in het midden van deze 2 x-waarden (symmetrie).
t = 3 invullen levert:
h(3) = -4,95 ⋅ (3)2 + 108,9 ⋅ 3 + 8000 = 8282,15
Dus de hoogte bij t = 3 is 8282,15 meter.
t = 19 invullen levert:
h(19) = -4,95 ⋅ (19)2 + 108,9 ⋅ 19 + 8000 = 8282,15
Dus de hoogte bij t = 19 is ook 8282,15 meter.
We hebben dus een symmetrie te pakken.
b.
Xtop is het midden tussen x = 3 en x = 19. Dus Xtop = 11.
Ytop wordt dan:
h(11) = -4,95 ⋅ (11)2 + 108,9 ⋅ 11 + 8000 = 8598,95
Dus de maximale hoogte (bij t = 11) is 8598,95 meter.
c.
De parabolische baan begint bij t = 0. De top ligt bij t = 11.
Dus bij t = 22 is de baan weer op z'n einde. Dus de baan duurt 22 seconden.
Andere paragrafen:
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


