TIP: Wil je ook toegang tot meer dan 16.900 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.5 Verschillende oplossingsmethoden VWO 3
Boek: Getal & Ruimte - Kwadratische problemen VWO 3 (deel 1) opgaven 53 t/m 60, 2011Er zijn 3 manieren om een kwadratische vergelijking op te lossen:
1) x2 = c, bijvoorbeeld x2 = 16 dan x = -4 of x = 4
2) Ontbinden in factoren, dus A x B = 0. Vaak gebruik je hier de product-som-methode of "haal x voor de haakjes".
3) De abc-formule
Maar welke moet je nu nemen? Probeer eerst of de 1e lukt, zo niet neem de 2e. Lukt dat niet, neem dan de abc-formule.
Schrijf een kwadratische vergelijking altijd naar de basisvorm ax2 + bx + c = 0.
1) x2 = c, bijvoorbeeld x2 = 16 dan x = -4 of x = 4
2) Ontbinden in factoren, dus A x B = 0. Vaak gebruik je hier de product-som-methode of "haal x voor de haakjes".
3) De abc-formule
Maar welke moet je nu nemen? Probeer eerst of de 1e lukt, zo niet neem de 2e. Lukt dat niet, neem dan de abc-formule.
Schrijf een kwadratische vergelijking altijd naar de basisvorm ax2 + bx + c = 0.
53.
x2 - 25 = 0
x2 = 25
x = 5 v x = -5
b.
(x - 1)(x + 3) = 0
x - 1 = 0 v x + 3 = 0
x = 1 v x = -3
54.
a.
x2 + 6x = 0 (haal x voor de haakjes)
x(x + 6) = 0
x = 0 v x + 6 = 0
x = 0 v x = -6
b.
x2 + 6x = 7
x2 + 6x - 7 = 0 (product-som-methode met -7)
(x - 1)(x + 7) = 0
x - 1 = 0 v x + 7 = 0
x = 1 v x = -7
c.
x2 + 6x + 7 = 0 (lukt niet met product-som-methode, dus abc-formule)
a = 1, b = 6 en c = 7
D = b2 - 4ac = (6)2 - 4 ⋅ 1 ⋅ 7 = 36 - 28 = 8
x1 = (-6 - √8) / 2 v x2 = (-6 + √8) / 2
x1 ≈ -4,41 v x2 ≈ -1,59
d.
6x2 + 36x = 96
6x2 + 36x - 96 = 0 (links en rechts :6)
x2 + 6x - 16 = 0 (product-som-methode met -16)
(x - 2)(x + 8) = 0
x - 2 = 0 v x + 8 = 0
x = 2 v x = -8
e.
x2 + 6 = 0
x2 = -6
Kan niet, dus geen oplossingen. Een kwadraat kan nooit negatief zijn.
f.
-x2 + 7x + 6 = 0
x2 - 7x - 6 = 0 (lukt niet met product-som-methode, dus abc-formule)
a = 1, b = -7 en c = -6
D = b2 - 4ac = (-7)2 - 4 ⋅ 1 ⋅ -6 = 49 + 24 = 73
x1 = (7 - √73) / 2 v x2 = (7 + √73) / 2
x1 ≈ -0,77 v x2 ≈ 7,77
55.
-x2 + 3x + 1 = 0
x2 - 3x - 1 = 0 (lukt niet met product-som-methode, dus abc-formule)
a = 1, b = -3 en c = -1
D = b2 - 4ac = (-3)2 - 4 ⋅ 1 ⋅ -1 = 9 + 4 = 13
x1 = (3 - √13) / 2 v x2 = (3 + √13) / 2
x1 ≈ -0,30 v x2 ≈ 3,30
b.
4x2 - 8x = 0 (haal 4x voor de haakjes)
4x(x - 2) = 0
4x = 0 v x - 2 = 0
x = 0 v x = 2
c.
4x2 + 4 = 8x
4x2 - 8x + 4 = 0 (links en rechts :4)
x2 - 2x + 1 = 0 (product-som-methode met +1)
(x - 1)(x - 1) = 0
x - 1 = 0 v x - 1 = 0
x = 1 v x = 1
d.
3x - 1 = 2x2
-2x2 + 3x - 1 = 0
a = -2, b = 3 en c = -1
D = b2 - 4ac = (3)2 - 4 ⋅ -2 ⋅ -1 = 9 - 8 = 1
x1 = (-3 - √1) / -4 v x2 = (-3 + √1) / -4
x1 = (-3 - 1) / -4 v x2 = (-3 + 1) / -4
x1 = -4/-4 = 1 v x2 = -2/-4 = 1/2
e.
1/2x2 + 5x = 12
1/2x2 + 5x - 12 = 0 (links en rechts keer 2)
x2 + 10x - 24 = 0 (product-som-methode met -24)
(x - 2)(x + 12) = 0
x - 2 = 0 v x + 12 = 0
x = 2 v x = -12
f.
(x - 2)(x - 3) = 20
x2 - 3x - 2x + 6 = 20
x2 - 5x - 14 = 0 (product-som-methode met -14)
(x + 2)(x - 7) = 0
x + 2 = 0 v x - 7 = 0
x = -2 v x = 7
56.
a.
(2x + 3)2 = 36 (van de vorm x2 = c)
2x + 3 = 6 v 2x + 3 = -6
2x = 3 v 2x = -9
x = 1½ v x = -4½
b.
(7x + 8)(3x - 57) = 0
7x + 8 = 0 v 3x - 57 = 0
7x = -8 v 3x = 57
x = -8/7 = -1 1/7 v x = 57/3 = 19
c.
1/15x2 + 1/5x = 1/3 (links en rechts keer 15)
x2 + 3x - 5 = 0
a = 1, b = 3 en c = -5
D = b2 - 4ac = (3)2 - 4 ⋅ 1 ⋅ -5 = 9 + 20 = 29
x1 = (-3 - √29) / 2 v x2 = (-3 + √29) / 2
x1 ≈ -4,19 v x2 ≈ 1,19
d.
(x - 1)(3x + 7) = -3
3x2 + 7x - 3x - 7 = -3
3x2 + 4x - 4 = 0
a = 3, b = 4 en c = -4
D = b2 - 4ac = (4)2 - 4 ⋅ 3 ⋅ -4 = 16 + 48 = 64
x1 = (-4 - √64) / 6 v x2 = (-4 + √64) / 6
x1 = (-4 - 8) / 6 v x2 = (-4 + 8) / 6
x1 = -12/6 = -2 v x2 = 4/6 = 2/3
e.
x(x - 1) = 1/5 - 4/5x
x2 - x = 1/5 - 4/5x (links en rechts keer 5)
5x2 - 5x = 1 - 4x
5x2 - x - 1 = 0
a = 5, b = -1 en c = -1
D = b2 - 4ac = (-1)2 - 4 ⋅ 5 ⋅ -1 = 1 + 20 = 21
x1 = (1 - √21) / 10 v x2 = (1 + √21) / 10
x1 ≈ -0,36 v x2 ≈ 0,56
f.
(3x - 1)2 - (2x + 1)2 = 7
9x2 - 6x + 1 - 4x2 - 4x - 1 = 7
5x2 - 10x - 7 = 0
a = 5, b = -10 en c = -7
D = b2 - 4ac = (-10)2 - 4 ⋅ 5 ⋅ -7 = 100 + 140 = 240
x1 = (10 - √240) / 10 v x2 = (10 + √240) / 10
x1 ≈ -0,55 v x2 ≈ 2,55
57.
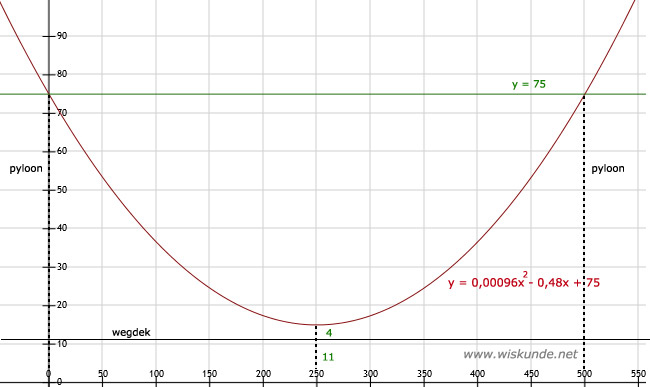
Los op: 0,00096x2 - 0,48x + 75 = 75
0,00096x2 - 0,48x = 0 (links en rechts :0,00096)
x2 - 500x = 0
x(x - 500) = 0
x = 0 v x - 500 = 0
x = 0 v x = 500
Dus de pylonen staan 500 meter uit elkaar.
b.
Het laagste punt bevindt zich bij de Xtop. De Xtop zit in het midden tussen 0 en 500.
Dus Xtop = 250.
Xtop invullen in de formule levert:
y = 0,00096 ⋅ (250)2 - 0,48 ⋅ 250 + 75
y = 60 - 120 + 75
y = 15
Dus het laagste punt (Ytop) is op 15 meter boven de fundering (x-as).
Het laagste punt tot de weg is 4 meter. Dus het wegdek hangt op hoogte 15 - 4 = 11 meter.
58.
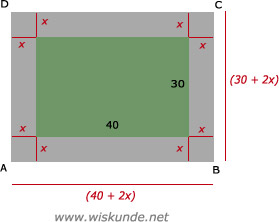
1200 + 80x + 60x + 4x2 = 3000
4x2 + 140x - 1800 = 0 (links en rechts :4)
x2 + 35x - 450 = 0 (product-som-methode met -450)
(x - 10)(x + 45) = 0
x - 10 = 0 v x + 45 = 0
x = 10 v x = -45
x = -45 kan niet want een negatieve afmeting bestaat niet.
Dus de lijst is 10 cm breed.
59.
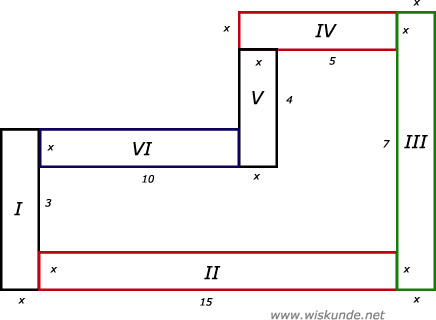
opp(II) = 15 ⋅ x = 15x
opp(III) = x ⋅ (7 + 2x) = 7x + 2x2
opp(IV) = x ⋅ (5 + x) = 5x + x2
opp(V) = 4 ⋅ x = 4x
opp(VI) = x ⋅ (10 - x) = 10x - x2
Tel nu alles op en je krijgt als totale oppervlakte: 4x2 + 44x
Dus oppervlakte tegelpad = 4x2 + 44x
4x2 + 44x = 104 (links en rechts :4)
x2 + 11x - 26 = 0 (product-som-methode met -26)
(x - 2)(x + 13) = 0
x - 2 = 0 v x + 13 = 0
x = 2 v x = -13
Dus breedte van het pad is 2 meter.
60.
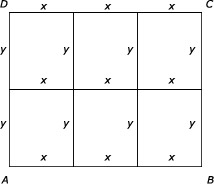
(1) 9x + 8y = 576
(2) x ⋅ y = 1152 => y = 1152/x
Vul y = 1152/x in (1) levert:
9x + 8 ⋅ (1152/x) = 576
9x + 9216/x = 576 (links en rechts keer x)
9x2 + 9216 = 576x
9x2 - 576x + 9216 = 0 (links en rechts :9)
x2 - 64x + 1024 = 0
a = 1, b = -64 en c = 1024
D = b2 - 4ac = (-64)2 - 4 ⋅ 1 ⋅ 1024 = 4096 - 4096 = 0
x1 = (64 - √0) / 2 v x2 = (64 + √0) / 2
x1 = 64/2 v x2 = 64/2
x1 = 32 v x2 = 32
Dus x = 32
x ⋅ y = 1152 => y = 1152/32 = 36
Dus x = 32 meter en y = 36 meter.
Tip:
Als x2 = c, dan x1 = √c of x2 = -√c
a.Als x2 = c, dan x1 = √c of x2 = -√c
x2 - 25 = 0
x2 = 25
x = 5 v x = -5
b.
(x - 1)(x + 3) = 0
x - 1 = 0 v x + 3 = 0
x = 1 v x = -3
54.
a.
x2 + 6x = 0 (haal x voor de haakjes)
x(x + 6) = 0
x = 0 v x + 6 = 0
x = 0 v x = -6
b.
x2 + 6x = 7
x2 + 6x - 7 = 0 (product-som-methode met -7)
(x - 1)(x + 7) = 0
x - 1 = 0 v x + 7 = 0
x = 1 v x = -7
c.
x2 + 6x + 7 = 0 (lukt niet met product-som-methode, dus abc-formule)
a = 1, b = 6 en c = 7
D = b2 - 4ac = (6)2 - 4 ⋅ 1 ⋅ 7 = 36 - 28 = 8
x1 = (-6 - √8) / 2 v x2 = (-6 + √8) / 2
x1 ≈ -4,41 v x2 ≈ -1,59
d.
6x2 + 36x = 96
6x2 + 36x - 96 = 0 (links en rechts :6)
x2 + 6x - 16 = 0 (product-som-methode met -16)
(x - 2)(x + 8) = 0
x - 2 = 0 v x + 8 = 0
x = 2 v x = -8
e.
x2 + 6 = 0
x2 = -6
Kan niet, dus geen oplossingen. Een kwadraat kan nooit negatief zijn.
f.
-x2 + 7x + 6 = 0
x2 - 7x - 6 = 0 (lukt niet met product-som-methode, dus abc-formule)
a = 1, b = -7 en c = -6
D = b2 - 4ac = (-7)2 - 4 ⋅ 1 ⋅ -6 = 49 + 24 = 73
x1 = (7 - √73) / 2 v x2 = (7 + √73) / 2
x1 ≈ -0,77 v x2 ≈ 7,77
55.
Tip:
Bij f: deze is niet van de vorm A x B = 0 want er staat '... = 20'. Dus werk de haakjes weg.
a. Bij f: deze is niet van de vorm A x B = 0 want er staat '... = 20'. Dus werk de haakjes weg.
-x2 + 3x + 1 = 0
x2 - 3x - 1 = 0 (lukt niet met product-som-methode, dus abc-formule)
a = 1, b = -3 en c = -1
D = b2 - 4ac = (-3)2 - 4 ⋅ 1 ⋅ -1 = 9 + 4 = 13
x1 = (3 - √13) / 2 v x2 = (3 + √13) / 2
x1 ≈ -0,30 v x2 ≈ 3,30
b.
4x2 - 8x = 0 (haal 4x voor de haakjes)
4x(x - 2) = 0
4x = 0 v x - 2 = 0
x = 0 v x = 2
c.
4x2 + 4 = 8x
4x2 - 8x + 4 = 0 (links en rechts :4)
x2 - 2x + 1 = 0 (product-som-methode met +1)
(x - 1)(x - 1) = 0
x - 1 = 0 v x - 1 = 0
x = 1 v x = 1
d.
3x - 1 = 2x2
-2x2 + 3x - 1 = 0
a = -2, b = 3 en c = -1
D = b2 - 4ac = (3)2 - 4 ⋅ -2 ⋅ -1 = 9 - 8 = 1
x1 = (-3 - √1) / -4 v x2 = (-3 + √1) / -4
x1 = (-3 - 1) / -4 v x2 = (-3 + 1) / -4
x1 = -4/-4 = 1 v x2 = -2/-4 = 1/2
e.
1/2x2 + 5x = 12
1/2x2 + 5x - 12 = 0 (links en rechts keer 2)
x2 + 10x - 24 = 0 (product-som-methode met -24)
(x - 2)(x + 12) = 0
x - 2 = 0 v x + 12 = 0
x = 2 v x = -12
f.
(x - 2)(x - 3) = 20
x2 - 3x - 2x + 6 = 20
x2 - 5x - 14 = 0 (product-som-methode met -14)
(x + 2)(x - 7) = 0
x + 2 = 0 v x - 7 = 0
x = -2 v x = 7
56.
a.
(2x + 3)2 = 36 (van de vorm x2 = c)
2x + 3 = 6 v 2x + 3 = -6
2x = 3 v 2x = -9
x = 1½ v x = -4½
b.
(7x + 8)(3x - 57) = 0
7x + 8 = 0 v 3x - 57 = 0
7x = -8 v 3x = 57
x = -8/7 = -1 1/7 v x = 57/3 = 19
c.
1/15x2 + 1/5x = 1/3 (links en rechts keer 15)
x2 + 3x - 5 = 0
a = 1, b = 3 en c = -5
D = b2 - 4ac = (3)2 - 4 ⋅ 1 ⋅ -5 = 9 + 20 = 29
x1 = (-3 - √29) / 2 v x2 = (-3 + √29) / 2
x1 ≈ -4,19 v x2 ≈ 1,19
d.
(x - 1)(3x + 7) = -3
3x2 + 7x - 3x - 7 = -3
3x2 + 4x - 4 = 0
a = 3, b = 4 en c = -4
D = b2 - 4ac = (4)2 - 4 ⋅ 3 ⋅ -4 = 16 + 48 = 64
x1 = (-4 - √64) / 6 v x2 = (-4 + √64) / 6
x1 = (-4 - 8) / 6 v x2 = (-4 + 8) / 6
x1 = -12/6 = -2 v x2 = 4/6 = 2/3
e.
x(x - 1) = 1/5 - 4/5x
x2 - x = 1/5 - 4/5x (links en rechts keer 5)
5x2 - 5x = 1 - 4x
5x2 - x - 1 = 0
a = 5, b = -1 en c = -1
D = b2 - 4ac = (-1)2 - 4 ⋅ 5 ⋅ -1 = 1 + 20 = 21
x1 = (1 - √21) / 10 v x2 = (1 + √21) / 10
x1 ≈ -0,36 v x2 ≈ 0,56
f.
(3x - 1)2 - (2x + 1)2 = 7
9x2 - 6x + 1 - 4x2 - 4x - 1 = 7
5x2 - 10x - 7 = 0
a = 5, b = -10 en c = -7
D = b2 - 4ac = (-10)2 - 4 ⋅ 5 ⋅ -7 = 100 + 140 = 240
x1 = (10 - √240) / 10 v x2 = (10 + √240) / 10
x1 ≈ -0,55 v x2 ≈ 2,55
57.
Tip:
Zie de x-as en y-as in het plaatje in je boek.
Bij a: Bereken de snijpunten van de parabool met de hoogte 75.
a.Zie de x-as en y-as in het plaatje in je boek.
Bij a: Bereken de snijpunten van de parabool met de hoogte 75.
Los op: 0,00096x2 - 0,48x + 75 = 75
0,00096x2 - 0,48x = 0 (links en rechts :0,00096)
x2 - 500x = 0
x(x - 500) = 0
x = 0 v x - 500 = 0
x = 0 v x = 500
Dus de pylonen staan 500 meter uit elkaar.
b.
Het laagste punt bevindt zich bij de Xtop. De Xtop zit in het midden tussen 0 en 500.
Dus Xtop = 250.
Xtop invullen in de formule levert:
y = 0,00096 ⋅ (250)2 - 0,48 ⋅ 250 + 75
y = 60 - 120 + 75
y = 15
Dus het laagste punt (Ytop) is op 15 meter boven de fundering (x-as).
Het laagste punt tot de weg is 4 meter. Dus het wegdek hangt op hoogte 15 - 4 = 11 meter.

58.
Tip:
oppervlakte(doek/groen) = 40% x oppervlakte(totaal ABCD)
1200 = 0,4 x oppervlakte(totaal)
oppervlakte(totaal) = 3000 cm2
oppervlakte(totaal) = lengte x breedte = (40 + 2x)(30 + 2x) = 3000oppervlakte(doek/groen) = 40% x oppervlakte(totaal ABCD)
1200 = 0,4 x oppervlakte(totaal)
oppervlakte(totaal) = 3000 cm2
1200 + 80x + 60x + 4x2 = 3000
4x2 + 140x - 1800 = 0 (links en rechts :4)
x2 + 35x - 450 = 0 (product-som-methode met -450)
(x - 10)(x + 45) = 0
x - 10 = 0 v x + 45 = 0
x = 10 v x = -45
x = -45 kan niet want een negatieve afmeting bestaat niet.
Dus de lijst is 10 cm breed.

59.
Tip:
Verdeel het tegelpad in rechthoeken.
opp(I) = x ⋅ (3 + 2x) = 3x + 2x2Verdeel het tegelpad in rechthoeken.
opp(II) = 15 ⋅ x = 15x
opp(III) = x ⋅ (7 + 2x) = 7x + 2x2
opp(IV) = x ⋅ (5 + x) = 5x + x2
opp(V) = 4 ⋅ x = 4x
opp(VI) = x ⋅ (10 - x) = 10x - x2
Tel nu alles op en je krijgt als totale oppervlakte: 4x2 + 44x
Dus oppervlakte tegelpad = 4x2 + 44x
4x2 + 44x = 104 (links en rechts :4)
x2 + 11x - 26 = 0 (product-som-methode met -26)
(x - 2)(x + 13) = 0
x - 2 = 0 v x + 13 = 0
x = 2 v x = -13
Dus breedte van het pad is 2 meter.

60.
Tip:
opp(ABCD) = 6912
opp(1 veld) = 6912 / 6 = 1152
Stel lengte 1 veld gelijk aan x en de breedte gelijk aan y
omtrek afrastering = 9x + 8y = 576
We hebben dus 2 vergelijkingen: opp(ABCD) = 6912
opp(1 veld) = 6912 / 6 = 1152
Stel lengte 1 veld gelijk aan x en de breedte gelijk aan y
omtrek afrastering = 9x + 8y = 576
(1) 9x + 8y = 576
(2) x ⋅ y = 1152 => y = 1152/x
Vul y = 1152/x in (1) levert:
9x + 8 ⋅ (1152/x) = 576
9x + 9216/x = 576 (links en rechts keer x)
9x2 + 9216 = 576x
9x2 - 576x + 9216 = 0 (links en rechts :9)
x2 - 64x + 1024 = 0
a = 1, b = -64 en c = 1024
D = b2 - 4ac = (-64)2 - 4 ⋅ 1 ⋅ 1024 = 4096 - 4096 = 0
x1 = (64 - √0) / 2 v x2 = (64 + √0) / 2
x1 = 64/2 v x2 = 64/2
x1 = 32 v x2 = 32
Dus x = 32
x ⋅ y = 1152 => y = 1152/32 = 36
Dus x = 32 meter en y = 36 meter.

Andere paragrafen:
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


