TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.4 De abc-formule VWO 3
Boek: Getal & Ruimte - Kwadratische problemen VWO 3 (deel 1) opgaven 36 t/m 52, 2011De abc-formule gebruiken we om kwadratische vergelijkingen op te lossen die niet op te lossen zijn met de product-som-methode. Vele vergelijkingen hebben als oplossing geen roosterpunten. Met de abc-formule kun je elke kwadratische vergelijking oplossen. Ook die wel met de product-som-methode zijn op te lossen.
De abc-formule:
x1 = -b + √D / 2a en x2 = -b - √D / 2a, met D = Discriminant = b2 - 4ac
Schrijf eerst de kwadratische vergelijking in de vorm: ax2 + bx + c = 0 en schrijf op wat a, b en c zijn en vul dan de abc-formule in.
De abc-formule:
x1 = -b + √D / 2a en x2 = -b - √D / 2a, met D = Discriminant = b2 - 4ac
Schrijf eerst de kwadratische vergelijking in de vorm: ax2 + bx + c = 0 en schrijf op wat a, b en c zijn en vul dan de abc-formule in.
36.
b. Snijpunten zijn A(1/3,0) en B(3 3/4,0).
37.
b. x2 - 3x - 8 = 0 => a = 1, b = -3, c = -8
c. x2 - 10x + 7 = 0 => a = 1, b = -10, c = 7
d. x2 + 7 = 0 => a = 1, b = 0, c = 7
38.
a = 3, b = -7 en c = 2
D = b2 - 4ac = (-7)2 - 4 ⋅ 3 ⋅ 2 = 49 - 24 = 25
x1 = (7 - √25) / 6 v x2 = (7 + √25) / 6
x1 = (7 - 5)/6 v x2 = (7 + 5)/6
x1 = 1/3 v x2 = 2
b.
a = 5, b = -1 en c = -4
D = b2 - 4ac = (-1)2 - 4 ⋅ 5 ⋅ -4 = 1 + 80 = 81
x1 = (1 - √81) / 10 v x2 = (1 + √81) / 10
x1 = (1 - 9)/10 v x2 = (1 + 9)/10
x1 = -4/5 v x2 = 1
c.
a = 10, b = 9 en c = 2
D = b2 - 4ac = (9)2 - 4 ⋅ 10 ⋅ 2 = 81 - 80 = 1
x1 = (-9 - √1) / 20 v x2 = (-9 + √1) / 20
x1 = (-9 - 1)/20 v x2 = (-9 + 1)/20
x1 = -1/2 v x2 = -2/5
d.
a = 4, b = 5 en c = 1
D = b2 - 4ac = (5)2 - 4 ⋅ 4 ⋅ 1 = 25 - 16 = 9
x1 = (-5 - √9) / 8 v x2 = (-5 + √9) / 8
x1 = (-5 - 3)/8 v x2 = (-5 + 3)/8
x1 = -1 v x2 = -1/4
e.
a = 2, b = 3 en c = -5
D = b2 - 4ac = (3)2 - 4 ⋅ 2 ⋅ -5 = 9 + 40 = 49
x1 = (-3 - √49) / 4 v x2 = (-3 + √49) / 4
x1 = (-3 - 7)/4 v x2 = (-3 + 7)/4
x1 = -2½ v x2 = 1
f.
a = 7, b = -5 en c = -2
D = b2 - 4ac = (-5)2 - 4 ⋅ 7 ⋅ -2 = 25 + 56 = 81
x1 = (5 - √81) / 14 v x2 = (5 + √81) / 14
x1 = (5 - 9)/14 v x2 = (5 + 9)/14
x1 = -2/7 v x2 = 1
39.
3x2 - 10x + 3 = 0
a = 3, b = -10 en c = 3
D = b2 - 4ac = (-10)2 - 4 ⋅ 3 ⋅ 3 = 100 - 36 = 64
x1 = (10 - √64) / 6 v x2 = (10 + √64) / 6
x1 = (10 - 8)/6 v x2 = (10 + 8)/6
x1 = 1/3 v x2 = 3
b.
6x2 + x - 2 = 0
a = 6, b = 1 en c = -2
D = b2 - 4ac = (1)2 - 4 ⋅ 6 ⋅ -2 = 1 + 48 = 49
x1 = (-1 - √49) / 12 v x2 = (-1 + √49) / 12
x1 = (-1 - 7)/12 v x2 = (-1 + 7)/12
x1 = -2/3 v x2 = 1/2
c.
4x2 - 8x + 3 = 0
a = 4, b = -8 en c = 3
D = b2 - 4ac = (-8)2 - 4 ⋅ 4 ⋅ 3 = 64 - 48 = 16
x1 = (8 - √16) / 8 v x2 = (8 + √16) / 8
x1 = (8 - 4)/8 v x2 = (8 + 4)/8
x1 = 1/2 v x2 = 1½
d.
2x2 - 7x + 5 = 0
a = 2, b = -7 en c = 5
D = b2 - 4ac = (-7)2 - 4 ⋅ 2 ⋅ 5 = 49 - 40 = 9
x1 = (7 - √9) / 4 v x2 = (7 + √9) / 4
x1 = (7 - 3)/4 v x2 = (7 + 3)/4
x1 = 1 v x2 = 2½
e.
5x2 - 9x + 4 = 0
a = 5, b = -9 en c = 4
D = b2 - 4ac = (-9)2 - 4 ⋅ 5 ⋅ 4 = 81 - 80 = 1
x1 = (9 - √1) / 10 v x2 = (9 + √1) / 10
x1 = (9 - 1)/10 v x2 = (9 + 1)/10
x1 = 4/5 v x2 = 1
f.
50x2 - 15x + 1 = 0
a = 50, b = -15 en c = 1
D = b2 - 4ac = (-15)2 - 4 ⋅ 50 ⋅ 1 = 225 - 200 = 25
x1 = (15 - √25) / 100 v x2 = (15 + √25) / 100
x1 = (15 - 5)/100 v x2 = (15 + 5)/100
x1 = 1/10 v x2 = 1/5
40.
a = 2, b = 4 en c = 1
D = b2 - 4ac = (4)2 - 4 ⋅ 2 ⋅ 1 = 16 - 8 = 8
x1 = (-4 - √8) / 4 v x2 = (-4 + √8) / 4
x1 ≈ -1,71 v x2 ≈ -0,29
b.
a = 1, b = 1 en c = -5
D = b2 - 4ac = (1)2 - 4 ⋅ 1 ⋅ -5 = 1 + 20 = 21
x1 = (-1 - √21) / 2 v x2 = (-1 + √21) / 2
x1 ≈ -2,79 v x2 ≈ 1,79
c.
a = 3, b = -2 en c = -8
D = b2 - 4ac = (-2)2 - 4 ⋅ 3 ⋅ -8 = 4 + 96 = 100
x1 = (2 - √100) / 6 v x2 = (2 + √100) / 6
x1 = (2 - 10) / 6 v x2 = (2 + 10) / 6
x1 = -4/3 v x2 = 2
d.
a = 2, b = 1 en c = 5
D = b2 - 4ac = (1)2 - 4 ⋅ 2 ⋅ 5 = 1 - 40 = -39
D < 0 dan geen oplossingen.
41.
a = 25, b = 20 en c = 1
D = b2 - 4ac = (20)2 - 4 ⋅ 25 ⋅ 1 = 400 - 100 = 300
x1 = (-20 - √300) / 50 v x2 = (-20 + √300) / 50
x1 ≈ -0,75 v x2 ≈ -0,05
b.
2x2 - 3x - 1 = 0
a = 2, b = -3 en c = -1
D = b2 - 4ac = (-3)2 - 4 ⋅ 2 ⋅ -1 = 9 + 8 = 17
x1 = (3 - √17) / 4 v x2 = (3 + √17) / 4
x1 ≈ -0,28 v x2 ≈ 1,78
c.
-2x2 + 5x - 2 = 0
a = -2, b = 5 en c = -2
D = b2 - 4ac = (5)2 - 4 ⋅ -2 ⋅ -2 = 25 - 16 = 9
x1 = (-5 - √9) / -4 v x2 = (-5 + √9) / -4
x1 = (-5 - 3) / -4 v x2 = (-5 + 3) / -4
x1 = -8/-4 = 2 v x2 = -2/-4 = 1/2
d.
a = -2, b = 12 en c = -18
D = b2 - 4ac = (12)2 - 4 ⋅ -2 ⋅ -18 = 144 - 144 = 0
x1 = (-12 - √0) / -4 v x2 = (-12 + √0) / -4
x1 = -12/-4 = 3 v x2 = -12/-4 = 3
42.
Snijpunten met de x-as: y = 0 ofwel f(x) = 0
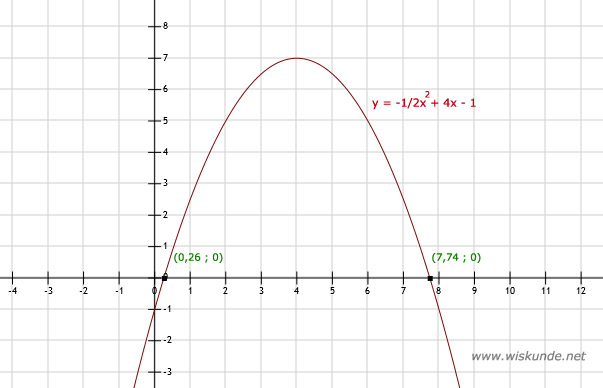
-1/2x2 + 4x - 1 = 0
a = -1/2, b = 4 en c = -1
D = b2 - 4ac = (4)2 - 4 ⋅ -1/2 ⋅ -1 = 16 - 2 = 14
x1 = (-4 - √14) / -1 v x2 = (-4 + √14) / -1
x1 ≈ 7,74 v x2 ≈ 0,26
Dus de snijpunten met de x-as zijn: (0,26 ; 0) en (7,74 ; 0).
43.
a = 1, b = -2 en c = 2
D = b2 - 4ac = (-2)2 - 4 ⋅ 1 ⋅ 2 = 4 - 8 = -4
b.
D < 0 dan zijn er geen oplossingen.
Het is een dalparabool die boven de x-as ligt. Dus geen snijpunten met de x-as.
c.
a = 0,5, b = -2 en c = 2
D = b2 - 4ac = (-2)2 - 4 ⋅ 0,5 ⋅ 2 = 4 - 4 = 0
d.
x1 = (2 - √0) / 1 v x2 = (2 + √0) / 1
x1 = 2 v x2 = 2
e.
Deze heeft precies 1 oplossing. De dalparabool raakt de x-as in precies 1 punt.
Dit is het punt (2,0).
44.
a.
a = 1, b = 2 en c = 3
D = b2 - 4ac = (2)2 - 4 ⋅ 1 ⋅ 3 = 4 - 12 = -8
D < 0 dus er zijn geen snijpunten met de x-as
b.
a = -1, b = -1 en c = 1
D = b2 - 4ac = (-1)2 - 4 ⋅ -1 ⋅ 1 = 1 + 4 = 5
D > 0 dus er zijn 2 snijpunten met de x-as
c.
a = 1, b = 9 en c = 20
D = b2 - 4ac = (9)2 - 4 ⋅ 1 ⋅ 20 = 81 - 80 = 1
D > 0 dus er zijn 2 snijpunten met de x-as
d.
a = 4, b = -4 en c = 1
D = b2 - 4ac = (-4)2 - 4 ⋅ 4 ⋅ 1 = 16 - 16 = 0
D = 0 dus er is precies 1 snijpunt met de x-as (raakpunt)
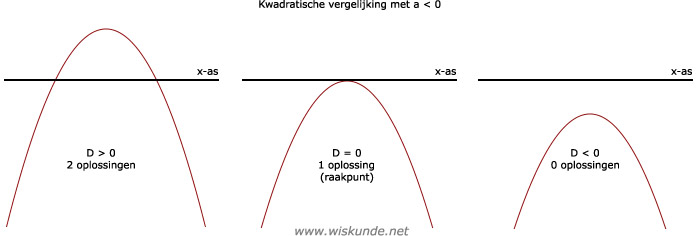
45.
Zie afbeelding
Tip:
Snijpunten van grafieken met de assen of andere grafieken zijn niet altijd mooie roosterpunten.
a. Er zijn geen 2 getallen (makkelijk) te vinden waarbij het product +1 is en de som -4.Snijpunten van grafieken met de assen of andere grafieken zijn niet altijd mooie roosterpunten.
b. Snijpunten zijn A(1/3,0) en B(3 3/4,0).
37.
Tip:
Werk eerst alle haken en kwadraten weg en werk naar de basisvorm ax2 + bx + c = 0.
a. x2 - 6x - 3 = 0 => a = 1, b = -6, c = -3Werk eerst alle haken en kwadraten weg en werk naar de basisvorm ax2 + bx + c = 0.
b. x2 - 3x - 8 = 0 => a = 1, b = -3, c = -8
c. x2 - 10x + 7 = 0 => a = 1, b = -10, c = 7
d. x2 + 7 = 0 => a = 1, b = 0, c = 7
38.
Tip:
Schrijf de a, b en c op en vul de abc-formule goed in.
a.Schrijf de a, b en c op en vul de abc-formule goed in.
a = 3, b = -7 en c = 2
D = b2 - 4ac = (-7)2 - 4 ⋅ 3 ⋅ 2 = 49 - 24 = 25
x1 = (7 - √25) / 6 v x2 = (7 + √25) / 6
x1 = (7 - 5)/6 v x2 = (7 + 5)/6
x1 = 1/3 v x2 = 2
b.
a = 5, b = -1 en c = -4
D = b2 - 4ac = (-1)2 - 4 ⋅ 5 ⋅ -4 = 1 + 80 = 81
x1 = (1 - √81) / 10 v x2 = (1 + √81) / 10
x1 = (1 - 9)/10 v x2 = (1 + 9)/10
x1 = -4/5 v x2 = 1
c.
a = 10, b = 9 en c = 2
D = b2 - 4ac = (9)2 - 4 ⋅ 10 ⋅ 2 = 81 - 80 = 1
x1 = (-9 - √1) / 20 v x2 = (-9 + √1) / 20
x1 = (-9 - 1)/20 v x2 = (-9 + 1)/20
x1 = -1/2 v x2 = -2/5
d.
a = 4, b = 5 en c = 1
D = b2 - 4ac = (5)2 - 4 ⋅ 4 ⋅ 1 = 25 - 16 = 9
x1 = (-5 - √9) / 8 v x2 = (-5 + √9) / 8
x1 = (-5 - 3)/8 v x2 = (-5 + 3)/8
x1 = -1 v x2 = -1/4
e.
a = 2, b = 3 en c = -5
D = b2 - 4ac = (3)2 - 4 ⋅ 2 ⋅ -5 = 9 + 40 = 49
x1 = (-3 - √49) / 4 v x2 = (-3 + √49) / 4
x1 = (-3 - 7)/4 v x2 = (-3 + 7)/4
x1 = -2½ v x2 = 1
f.
a = 7, b = -5 en c = -2
D = b2 - 4ac = (-5)2 - 4 ⋅ 7 ⋅ -2 = 25 + 56 = 81
x1 = (5 - √81) / 14 v x2 = (5 + √81) / 14
x1 = (5 - 9)/14 v x2 = (5 + 9)/14
x1 = -2/7 v x2 = 1
39.
Tip:
Schrijf eerst naar de vorm ax2 + bx + c = 0.
a.Schrijf eerst naar de vorm ax2 + bx + c = 0.
3x2 - 10x + 3 = 0
a = 3, b = -10 en c = 3
D = b2 - 4ac = (-10)2 - 4 ⋅ 3 ⋅ 3 = 100 - 36 = 64
x1 = (10 - √64) / 6 v x2 = (10 + √64) / 6
x1 = (10 - 8)/6 v x2 = (10 + 8)/6
x1 = 1/3 v x2 = 3
b.
6x2 + x - 2 = 0
a = 6, b = 1 en c = -2
D = b2 - 4ac = (1)2 - 4 ⋅ 6 ⋅ -2 = 1 + 48 = 49
x1 = (-1 - √49) / 12 v x2 = (-1 + √49) / 12
x1 = (-1 - 7)/12 v x2 = (-1 + 7)/12
x1 = -2/3 v x2 = 1/2
c.
4x2 - 8x + 3 = 0
a = 4, b = -8 en c = 3
D = b2 - 4ac = (-8)2 - 4 ⋅ 4 ⋅ 3 = 64 - 48 = 16
x1 = (8 - √16) / 8 v x2 = (8 + √16) / 8
x1 = (8 - 4)/8 v x2 = (8 + 4)/8
x1 = 1/2 v x2 = 1½
d.
2x2 - 7x + 5 = 0
a = 2, b = -7 en c = 5
D = b2 - 4ac = (-7)2 - 4 ⋅ 2 ⋅ 5 = 49 - 40 = 9
x1 = (7 - √9) / 4 v x2 = (7 + √9) / 4
x1 = (7 - 3)/4 v x2 = (7 + 3)/4
x1 = 1 v x2 = 2½
e.
5x2 - 9x + 4 = 0
a = 5, b = -9 en c = 4
D = b2 - 4ac = (-9)2 - 4 ⋅ 5 ⋅ 4 = 81 - 80 = 1
x1 = (9 - √1) / 10 v x2 = (9 + √1) / 10
x1 = (9 - 1)/10 v x2 = (9 + 1)/10
x1 = 4/5 v x2 = 1
f.
50x2 - 15x + 1 = 0
a = 50, b = -15 en c = 1
D = b2 - 4ac = (-15)2 - 4 ⋅ 50 ⋅ 1 = 225 - 200 = 25
x1 = (15 - √25) / 100 v x2 = (15 + √25) / 100
x1 = (15 - 5)/100 v x2 = (15 + 5)/100
x1 = 1/10 v x2 = 1/5
40.
Tip:
Als D < 0 dan zijn er geen oplossingen
Als D = 0 dan is er precies 1 oplossing
Als D > 0 dan zijn er 2 oplossingen
a.Als D < 0 dan zijn er geen oplossingen
Als D = 0 dan is er precies 1 oplossing
Als D > 0 dan zijn er 2 oplossingen
a = 2, b = 4 en c = 1
D = b2 - 4ac = (4)2 - 4 ⋅ 2 ⋅ 1 = 16 - 8 = 8
x1 = (-4 - √8) / 4 v x2 = (-4 + √8) / 4
x1 ≈ -1,71 v x2 ≈ -0,29
b.
a = 1, b = 1 en c = -5
D = b2 - 4ac = (1)2 - 4 ⋅ 1 ⋅ -5 = 1 + 20 = 21
x1 = (-1 - √21) / 2 v x2 = (-1 + √21) / 2
x1 ≈ -2,79 v x2 ≈ 1,79
c.
a = 3, b = -2 en c = -8
D = b2 - 4ac = (-2)2 - 4 ⋅ 3 ⋅ -8 = 4 + 96 = 100
x1 = (2 - √100) / 6 v x2 = (2 + √100) / 6
x1 = (2 - 10) / 6 v x2 = (2 + 10) / 6
x1 = -4/3 v x2 = 2
d.
a = 2, b = 1 en c = 5
D = b2 - 4ac = (1)2 - 4 ⋅ 2 ⋅ 5 = 1 - 40 = -39
D < 0 dan geen oplossingen.
41.
Tip:
Bij opgave d: D = 0 en je ziet dat er inderdaad maar 1 oplossing is: x = 3
a.Bij opgave d: D = 0 en je ziet dat er inderdaad maar 1 oplossing is: x = 3
a = 25, b = 20 en c = 1
D = b2 - 4ac = (20)2 - 4 ⋅ 25 ⋅ 1 = 400 - 100 = 300
x1 = (-20 - √300) / 50 v x2 = (-20 + √300) / 50
x1 ≈ -0,75 v x2 ≈ -0,05
b.
2x2 - 3x - 1 = 0
a = 2, b = -3 en c = -1
D = b2 - 4ac = (-3)2 - 4 ⋅ 2 ⋅ -1 = 9 + 8 = 17
x1 = (3 - √17) / 4 v x2 = (3 + √17) / 4
x1 ≈ -0,28 v x2 ≈ 1,78
c.
-2x2 + 5x - 2 = 0
a = -2, b = 5 en c = -2
D = b2 - 4ac = (5)2 - 4 ⋅ -2 ⋅ -2 = 25 - 16 = 9
x1 = (-5 - √9) / -4 v x2 = (-5 + √9) / -4
x1 = (-5 - 3) / -4 v x2 = (-5 + 3) / -4
x1 = -8/-4 = 2 v x2 = -2/-4 = 1/2
d.
a = -2, b = 12 en c = -18
D = b2 - 4ac = (12)2 - 4 ⋅ -2 ⋅ -18 = 144 - 144 = 0
x1 = (-12 - √0) / -4 v x2 = (-12 + √0) / -4
x1 = -12/-4 = 3 v x2 = -12/-4 = 3
42.
Snijpunten met de x-as: y = 0 ofwel f(x) = 0
-1/2x2 + 4x - 1 = 0
a = -1/2, b = 4 en c = -1
D = b2 - 4ac = (4)2 - 4 ⋅ -1/2 ⋅ -1 = 16 - 2 = 14
x1 = (-4 - √14) / -1 v x2 = (-4 + √14) / -1
x1 ≈ 7,74 v x2 ≈ 0,26
Dus de snijpunten met de x-as zijn: (0,26 ; 0) en (7,74 ; 0).

43.
Tip:
Als D = 0 dan raakt de parabool de x-as in 1 punt. We noemen dit het raakpunt.
a.Als D = 0 dan raakt de parabool de x-as in 1 punt. We noemen dit het raakpunt.
a = 1, b = -2 en c = 2
D = b2 - 4ac = (-2)2 - 4 ⋅ 1 ⋅ 2 = 4 - 8 = -4
b.
D < 0 dan zijn er geen oplossingen.
Het is een dalparabool die boven de x-as ligt. Dus geen snijpunten met de x-as.
c.
a = 0,5, b = -2 en c = 2
D = b2 - 4ac = (-2)2 - 4 ⋅ 0,5 ⋅ 2 = 4 - 4 = 0
d.
x1 = (2 - √0) / 1 v x2 = (2 + √0) / 1
x1 = 2 v x2 = 2
e.
Deze heeft precies 1 oplossing. De dalparabool raakt de x-as in precies 1 punt.
Dit is het punt (2,0).
44.
a.
a = 1, b = 2 en c = 3
D = b2 - 4ac = (2)2 - 4 ⋅ 1 ⋅ 3 = 4 - 12 = -8
D < 0 dus er zijn geen snijpunten met de x-as
b.
a = -1, b = -1 en c = 1
D = b2 - 4ac = (-1)2 - 4 ⋅ -1 ⋅ 1 = 1 + 4 = 5
D > 0 dus er zijn 2 snijpunten met de x-as
c.
a = 1, b = 9 en c = 20
D = b2 - 4ac = (9)2 - 4 ⋅ 1 ⋅ 20 = 81 - 80 = 1
D > 0 dus er zijn 2 snijpunten met de x-as
d.
a = 4, b = -4 en c = 1
D = b2 - 4ac = (-4)2 - 4 ⋅ 4 ⋅ 1 = 16 - 16 = 0
D = 0 dus er is precies 1 snijpunt met de x-as (raakpunt)
45.
Zie afbeelding

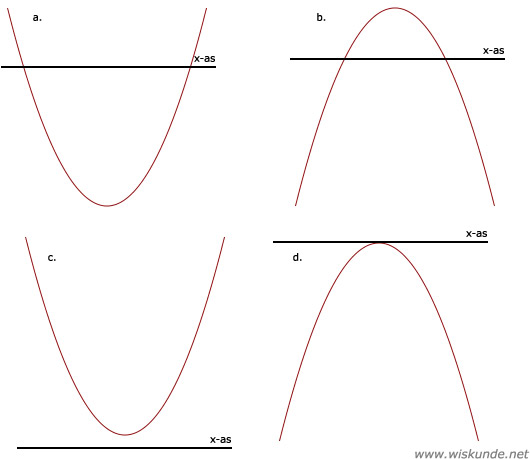
46.
a = 2, b = 3 en c = -4
D = b2 - 4ac = (3)2 - 4 ⋅ 2 ⋅ -4 = 9 + 32 = 41
D > 0 dus er zijn 2 snijpunten met de x-as en het is een dalparabool want a > 0
b.
a = -1, b = 6 en c = 1
D = b2 - 4ac = (6)2 - 4 ⋅ -1 ⋅ 1 = 36 + 4 = 40
D > 0 dus er zijn 2 snijpunten met de x-as en het is een bergparabool want a < 0
c.
a = 8, b = -1 en c = 1
D = b2 - 4ac = (-1)2 - 4 ⋅ 8 ⋅ 1 = 1 - 32 = -31
D < 0 dus er zijn geen snijpunten met de x-as en het is een dalparabool want a > 0
d.
a = -4, b = 6 en c = -2 1/4
D = b2 - 4ac = (6)2 - 4 ⋅ -4 ⋅ -2 1/4 = 36 - 36 = 0
D = 0 dus er is 1 snijpunt met de x-as en het is een bergparabool want a < 0
47.
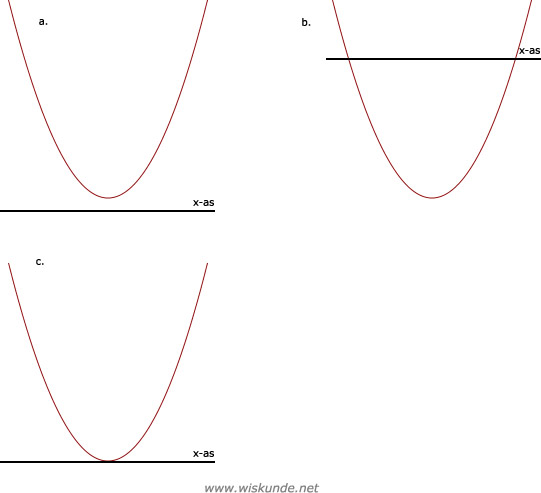
f(x) = x2 + 4x + 6
a = 1, b = 4 en c = 6
D = b2 - 4ac = (4)2 - 4 ⋅ 1 ⋅ 6 = 16 - 24 = -8
D < 0 dus er zijn geen snijpunten met de x-as en het is een dalparabool want a > 0
b.
f(x) = x2 + 4x - 3
a = 1, b = 4 en c = -3
D = b2 - 4ac = (4)2 - 4 ⋅ 1 ⋅ -3 = 16 + 12 = 28
D > 0 dus er zijn 2 snijpunten met de x-as en het is een dalparabool want a > 0
c.
f(x) = x2 + 4x + 4
a = 1, b = 4 en c = 4
D = b2 - 4ac = (4)2 - 4 ⋅ 1 ⋅ 4 = 16 - 16 = 0
D = 0 dus er is 1 snijpunt met de x-as en het is een dalparabool want a > 0
48.
f(x) = 2x2 - x + p
a = 2, b = -1 en c = p
D = b2 - 4ac = (-1)2 - 4 ⋅ 2 ⋅ p = 1 - 8p
Als D = 0 dan is er precies 1 snijpunt met de x-as.
Dus stel D = 0 levert:
1 - 8p = 0
-8p = -1
p = -1/-8 = 1/8
Dus als p = 1/8 dan hebben we de parabool 2x2 - x + 1/8 en deze heeft dan 1 snijpunt met de x-as.
b.
Geen snijpunten met de x-as => D < 0
1 - 8p < 0
-8p < -1
p > 1/8
Dus als p > 1/8 dan heeft de parabool geen snijpunten met de x-as.
c.
Vul in A(-3,15) in f(x) levert:
f(-3) = 2 ⋅ (-3)2 - (-3) + p = 15
2 ⋅ 9 + 3 + p = 15
18 + 3 + p = 15
21 + p = 15
p = -6
Dus voor p = -6 ligt A(-3,15) op de grafiek.
49.
a.
Als D = 0 dan is er precies 1 snijpunt met de x-as (raakpunt).
a = -1, b = 6 en c = p
D = b2 - 4ac = (6)2 - 4 ⋅ -1 ⋅ p = 36 + 4p
Dus los op: D = 0 =>
36 + 4p = 0
4p = -36
p = -36/4 = -9
Dus als p = -9 dan is er 1 snijpunt met de x-as en raakt de grafiek dus de x-as.
b.
Geen snijpunten met de x-as, dan moet gelden: D < 0.
36 + 4p < 0
4p < -36
p < -36/4
p < -9
Dus als p < -9 dan heeft de grafiek geen snijpunten met de x-as en ligt dus volledig onder de x-as (bergparabool).
c.
f(3) = -(3)2 + 6 ⋅ 3 + p = 8
-9 + 18 + p = 8
9 + p = 8
p = -1
Dus als p = -1 dan ligt het punt A(3,8) op de grafiek.
50.
Geheel onder de x-as d.w.z geen snijpunten met de x-as. Dus D < 0.
a = -3, b = 12 en c = p
D = b2 - 4ac = (12)2 - 4 ⋅ -3 ⋅ p = 144 + 12p
Dus los op: D < 0 =>
144 + 12p < 0
12p < -144
p < -144/12
p < -12
Dus als p < -12 dan ligt de grafiek onder de x-as.
b.
f(-8) = -3 ⋅ (-8)2 + 12 ⋅ -8 + p = 100
-3 ⋅ 64 - 96 + p = 100
-192 - 96 + p = 100
-288 + p = 100
p = 388
Dus voor p = 388 ligt het punt A(-8,100) op de grafiek.
c.
Snijpunt met de y-as: f(0) = -0 + 0 + p = p. Dus snijpunt is (0,p).
Dit snijpunt ligt onder de x-as als p < 0.
d.
f(1) = -3 ⋅ (1)2 + 12 ⋅ 1 + p = 0
-3 ⋅ 1 + 12 + p = 0
-3 + 12 + p = 0
9 + p = 0
p = -9
Je krijgt dus de functie f(x) = -3x2 + 12x - 9.
Nu los op voor snijpunten van f(x) met de x-as: f(x) = 0.
-3x2 + 12x - 9 = 0 (links en rechts :-3)
x2 - 4x + 3 = 0
(x - 1)(x - 3) = 0
x - 1 = 0 v x - 3 = 0
x = 1 v x = 3
Dus de snijpunten met de x-as zijn: (1,0) en (3,0).
Dus het punt C is (3,0).
51.
Als A(p,7) op de grafiek ligt dan moet gelden f(p) = 7.
f(p) = 3p2 + p ⋅ p + 3 = 7
3p2 + p2 + 3 = 7
4p2 + 3 = 7
4p2 = 4
p2 = 4/4
p2 = 1
p = 1 v p = -1
Dus voor p = 1 of p = -1 ligt punt (1,7) en punt (-1,7) op de grafiek.
b.
a > 0 dus een dalparabool
a = 3, b = p en c = 3
D = b2 - 4ac = (p)2 - 4 ⋅ 3 ⋅ 3 = p2 - 36
Als er sprake moet zijn van 1 snijpunt met de x-as, dan moet D = 0 zijn.
Dus los op: D = 0 =>
p2 - 36 = 0
p2 = 36
p = 6 v p = -6
Dus voor p = 6 of p = -6 ligt de top van de parabool op de x-as.
52.
px2 + 3x + px - 1 = 0
px2 + (3 + p)x - 1 = 0
a = p, b = (3 + p) en c = -1
D = b2 - 4ac = (3 + p)2 - 4 ⋅ p ⋅ -1 = 9 + 6p + p2 + 4p
D = p2 + 10p + 9
D = 0 stellen, levert:
p2 + 10p + 9 = 0
(p + 1)(p + 9) = 0
p + 1 = 0 v p + 9 = 0
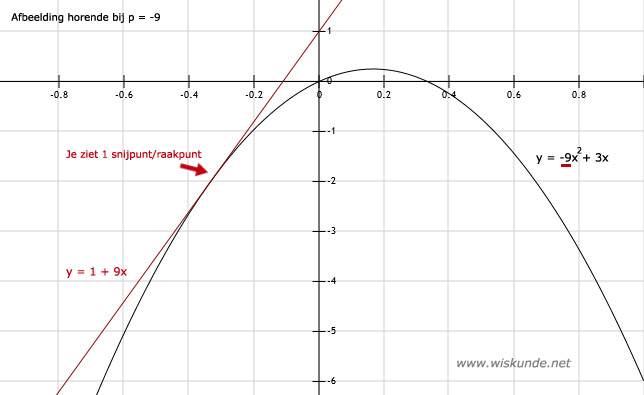
p = -1 v p = -9 (zie afbeelding als p = -9)
Tip:
Als a > 0 dan is het een dalparabool
Als a < 0 dan is het een bergparabool
a.Als a > 0 dan is het een dalparabool
Als a < 0 dan is het een bergparabool
a = 2, b = 3 en c = -4
D = b2 - 4ac = (3)2 - 4 ⋅ 2 ⋅ -4 = 9 + 32 = 41
D > 0 dus er zijn 2 snijpunten met de x-as en het is een dalparabool want a > 0
b.
a = -1, b = 6 en c = 1
D = b2 - 4ac = (6)2 - 4 ⋅ -1 ⋅ 1 = 36 + 4 = 40
D > 0 dus er zijn 2 snijpunten met de x-as en het is een bergparabool want a < 0
c.
a = 8, b = -1 en c = 1
D = b2 - 4ac = (-1)2 - 4 ⋅ 8 ⋅ 1 = 1 - 32 = -31
D < 0 dus er zijn geen snijpunten met de x-as en het is een dalparabool want a > 0
d.
a = -4, b = 6 en c = -2 1/4
D = b2 - 4ac = (6)2 - 4 ⋅ -4 ⋅ -2 1/4 = 36 - 36 = 0
D = 0 dus er is 1 snijpunt met de x-as en het is een bergparabool want a < 0

47.
Tip:
Voor iedere andere waarde van p krijg je dus steeds een andere parabool. Deze heeft dezelfde ligging maar zal verschuiven langs een verticale as.
a.Voor iedere andere waarde van p krijg je dus steeds een andere parabool. Deze heeft dezelfde ligging maar zal verschuiven langs een verticale as.
f(x) = x2 + 4x + 6
a = 1, b = 4 en c = 6
D = b2 - 4ac = (4)2 - 4 ⋅ 1 ⋅ 6 = 16 - 24 = -8
D < 0 dus er zijn geen snijpunten met de x-as en het is een dalparabool want a > 0
b.
f(x) = x2 + 4x - 3
a = 1, b = 4 en c = -3
D = b2 - 4ac = (4)2 - 4 ⋅ 1 ⋅ -3 = 16 + 12 = 28
D > 0 dus er zijn 2 snijpunten met de x-as en het is een dalparabool want a > 0
c.
f(x) = x2 + 4x + 4
a = 1, b = 4 en c = 4
D = b2 - 4ac = (4)2 - 4 ⋅ 1 ⋅ 4 = 16 - 16 = 0
D = 0 dus er is 1 snijpunt met de x-as en het is een dalparabool want a > 0

48.
Tip:
Als een punt A(-3,15) op de functie van f(x) moet liggen, dan moet gelden f(-3) = 15.
a.Als een punt A(-3,15) op de functie van f(x) moet liggen, dan moet gelden f(-3) = 15.
f(x) = 2x2 - x + p
a = 2, b = -1 en c = p
D = b2 - 4ac = (-1)2 - 4 ⋅ 2 ⋅ p = 1 - 8p
Als D = 0 dan is er precies 1 snijpunt met de x-as.
Dus stel D = 0 levert:
1 - 8p = 0
-8p = -1
p = -1/-8 = 1/8
Dus als p = 1/8 dan hebben we de parabool 2x2 - x + 1/8 en deze heeft dan 1 snijpunt met de x-as.
b.
Geen snijpunten met de x-as => D < 0
1 - 8p < 0
-8p < -1
p > 1/8
Dus als p > 1/8 dan heeft de parabool geen snijpunten met de x-as.
c.
Vul in A(-3,15) in f(x) levert:
f(-3) = 2 ⋅ (-3)2 - (-3) + p = 15
2 ⋅ 9 + 3 + p = 15
18 + 3 + p = 15
21 + p = 15
p = -6
Dus voor p = -6 ligt A(-3,15) op de grafiek.
49.
a.
Als D = 0 dan is er precies 1 snijpunt met de x-as (raakpunt).
a = -1, b = 6 en c = p
D = b2 - 4ac = (6)2 - 4 ⋅ -1 ⋅ p = 36 + 4p
Dus los op: D = 0 =>
36 + 4p = 0
4p = -36
p = -36/4 = -9
Dus als p = -9 dan is er 1 snijpunt met de x-as en raakt de grafiek dus de x-as.
b.
Geen snijpunten met de x-as, dan moet gelden: D < 0.
36 + 4p < 0
4p < -36
p < -36/4
p < -9
Dus als p < -9 dan heeft de grafiek geen snijpunten met de x-as en ligt dus volledig onder de x-as (bergparabool).
c.
f(3) = -(3)2 + 6 ⋅ 3 + p = 8
-9 + 18 + p = 8
9 + p = 8
p = -1
Dus als p = -1 dan ligt het punt A(3,8) op de grafiek.
50.
Tip:
B(1,0) ligt op de grafiek, dus vul in f(1) = 0 en bepaal daarna p. Bereken daarna f(x) = 0 voor snijpunten met de x-as. Zo vind je punt C.
a.B(1,0) ligt op de grafiek, dus vul in f(1) = 0 en bepaal daarna p. Bereken daarna f(x) = 0 voor snijpunten met de x-as. Zo vind je punt C.
Geheel onder de x-as d.w.z geen snijpunten met de x-as. Dus D < 0.
a = -3, b = 12 en c = p
D = b2 - 4ac = (12)2 - 4 ⋅ -3 ⋅ p = 144 + 12p
Dus los op: D < 0 =>
144 + 12p < 0
12p < -144
p < -144/12
p < -12
Dus als p < -12 dan ligt de grafiek onder de x-as.
b.
f(-8) = -3 ⋅ (-8)2 + 12 ⋅ -8 + p = 100
-3 ⋅ 64 - 96 + p = 100
-192 - 96 + p = 100
-288 + p = 100
p = 388
Dus voor p = 388 ligt het punt A(-8,100) op de grafiek.
c.
Snijpunt met de y-as: f(0) = -0 + 0 + p = p. Dus snijpunt is (0,p).
Dit snijpunt ligt onder de x-as als p < 0.
d.
f(1) = -3 ⋅ (1)2 + 12 ⋅ 1 + p = 0
-3 ⋅ 1 + 12 + p = 0
-3 + 12 + p = 0
9 + p = 0
p = -9
Je krijgt dus de functie f(x) = -3x2 + 12x - 9.
Nu los op voor snijpunten van f(x) met de x-as: f(x) = 0.
-3x2 + 12x - 9 = 0 (links en rechts :-3)
x2 - 4x + 3 = 0
(x - 1)(x - 3) = 0
x - 1 = 0 v x - 3 = 0
x = 1 v x = 3
Dus de snijpunten met de x-as zijn: (1,0) en (3,0).
Dus het punt C is (3,0).
51.
Tip:
Bij a: vul A(p,7) in f(x) en bepaal voor welke p het klopt.
Bij b: Ligt de top van een parabool op de x-as dan betekent dat dus dat er precies 1 snijpunt is met de x-as. Dus D = 0.
a.Bij a: vul A(p,7) in f(x) en bepaal voor welke p het klopt.
Bij b: Ligt de top van een parabool op de x-as dan betekent dat dus dat er precies 1 snijpunt is met de x-as. Dus D = 0.
Als A(p,7) op de grafiek ligt dan moet gelden f(p) = 7.
f(p) = 3p2 + p ⋅ p + 3 = 7
3p2 + p2 + 3 = 7
4p2 + 3 = 7
4p2 = 4
p2 = 4/4
p2 = 1
p = 1 v p = -1
Dus voor p = 1 of p = -1 ligt punt (1,7) en punt (-1,7) op de grafiek.
b.
a > 0 dus een dalparabool
a = 3, b = p en c = 3
D = b2 - 4ac = (p)2 - 4 ⋅ 3 ⋅ 3 = p2 - 36
Als er sprake moet zijn van 1 snijpunt met de x-as, dan moet D = 0 zijn.
Dus los op: D = 0 =>
p2 - 36 = 0
p2 = 36
p = 6 v p = -6
Dus voor p = 6 of p = -6 ligt de top van de parabool op de x-as.
52.
Tip:
Er wordt dus gevraagd voor welke p hebben de parabool en de lijn 1 snijpunt.
Dus dat de lijn de parabool raakt. Bepaal dus D = 0.
px2 + 3x = 1 - pxEr wordt dus gevraagd voor welke p hebben de parabool en de lijn 1 snijpunt.
Dus dat de lijn de parabool raakt. Bepaal dus D = 0.
px2 + 3x + px - 1 = 0
px2 + (3 + p)x - 1 = 0
a = p, b = (3 + p) en c = -1
D = b2 - 4ac = (3 + p)2 - 4 ⋅ p ⋅ -1 = 9 + 6p + p2 + 4p
D = p2 + 10p + 9
D = 0 stellen, levert:
p2 + 10p + 9 = 0
(p + 1)(p + 9) = 0
p + 1 = 0 v p + 9 = 0
p = -1 v p = -9 (zie afbeelding als p = -9)

Andere paragrafen:
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


