TIP: Wil je ook toegang tot meer dan 16.900 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.2 Kwadratische vergelijkingen VWO 3
Boek: Getal & Ruimte - Kwadratische problemen VWO 3 (deel 1) opgaven 13 t/m 26, 2011Hoe lossen we kwadratische vergelijkingen op?
Voorbeelden van kwadratische vergelijkingen zijn: x2 + 3x + 2 = 0 of (x + 7)(x - 3) = -23.
De oplossingen zijn de x-coördinaten van de snijpunten van de parabool met de x-as.
Om de oplossingen te vinden, gebruiken we 2 manieren:
1) Breng een zo groot mogelijke gemeenschappelijke factor voor de haakjes, bijvoorbeeld: 2x(x + 1) = 0
2) De product-som-methode (maak een T-tabel van het getal zonder een x)
Als de kwadratische vergelijking ontbonden is in factoren gebruik: Als A x B = 0 dan A = 0 of B = 0
Voorbeelden van kwadratische vergelijkingen zijn: x2 + 3x + 2 = 0 of (x + 7)(x - 3) = -23.
De oplossingen zijn de x-coördinaten van de snijpunten van de parabool met de x-as.
Om de oplossingen te vinden, gebruiken we 2 manieren:
1) Breng een zo groot mogelijke gemeenschappelijke factor voor de haakjes, bijvoorbeeld: 2x(x + 1) = 0
2) De product-som-methode (maak een T-tabel van het getal zonder een x)
Als de kwadratische vergelijking ontbonden is in factoren gebruik: Als A x B = 0 dan A = 0 of B = 0
13.
a. x(x + 6)
b. 5x(x - 4)
c. -x(x + 8)
d. x(x - 1)
14.
b. (x + 2)(x + 7)
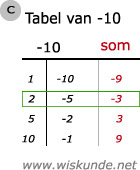
c. (x + 2)(x - 5) (zie afbeelding met een T-tabel van -10)
d. (x + 3)(x - 2)
15.
b. (x + 1)(x - 2)
c. (x + 5)(x - 7)
d. a(a + 4)
e. (p + 1)(p + 14)
f. (q - 8)(q + 9)
16.
x2 + 7x - 8 = 0 (product-som-methode met -8)
(x - 1)(x + 8) = 0
x - 1 = 0 v x + 8 = 0
x = 1 v x = -8
b.
2x2 - 6x = 0 (haal 2x voor de haakjes)
2x(x - 3) = 0
2x = 0 v x - 3 = 0
x = 0 v x = 3
c.
x2 - x = 0 (haal x voor de haakjes)
x(x - 1) = 0
x = 0 v x - 1 = 0
x = 0 v x = 1
d.
x2 - 6x + 5 = 0 (product-som-methode met 5)
(x - 1)(x - 5) = 0
x - 1 = 0 v x - 5 = 0
x = 1 v x = 5
e.
(is al ontbonden in factoren)
x - 1 = 0 v x + 3 = 0
x = 1 v x = -3
f.
x2 - 4x + 4 = 0 (product-som-methode met 4)
(x - 2)(x - 2) = 0
x - 2 = 0 v x - 2 = 0
x = 2 v x = 2
17.
x2 - 16x - 36 = 0 (product-som-methode met -36)
(x + 2)(x - 18) = 0
x + 2 = 0 v x - 18 = 0
x = -2 v x = 18
b.
-p2 - 11p = 0 (links en rechts maal -1)
p2 + 11p = 0 (haal p voor de haakjes)
p(p + 11) = 0
p = 0 v p + 11 = 0
p = 0 v p = -11
c.
a2 - 18a + 45 = 0 (product-som-methode met 45)
(a - 3)(a - 15) = 0
a - 3 = 0 v a - 15 = 0
a = 3 v a = 15
18.
x2 + x = 5x (links en rechts -5x)
x2 + x - 5x = 0
x2 - 4x = 0 (haal x voor de haakjes)
x(x - 4) = 0
x = 0 v x - 4 = 0
x = 0 v x = 4
b.
x2 + 6x + 9 = 2x + 9 (links en rechts -2x)
x2 + 6x - 2x + 9 = 9
x2 + 4x + 9 = 9 (links en rechts -9)
x2 + 4x = 0
x(x + 4) = 0
x = 0 v x + 4 = 0
x = 0 v x = -4
c.
(staat al goed ontbonden in factoren)
2t - 1 = 0 v t + 2 = 0
2t = 1 v t = -2
t = 1/2 v t = -2
d.
p2 + 2p - p - 2 = 10
p2 + p - 12 = 0 (product-som-methode met -12)
(p + 4)(p - 3) = 0 (nu is de vergelijking wel van de vorm A x B = 0)
p + 4 = 0 v p - 3 = 0
p = -4 v p = 3
19.
(deze is al goed ontbonden in factoren, want is van de vorm: A x B = 0)
3x - 1 = 0 v 5x + 30 = 0
3x = 1 v 5x = -30
x = 1/3 v x = -6
b.
x2 - 10x + 25 = 2x - 10
x2 - 12x + 35 = 0 (product-som-methode met +35)
(x - 5)(x - 7) = 0
x - 5 = 0 v x - 7 = 0
x = 5 v x = 7
c.
x2 - 2x + 1 - 6(x - 2) = 3x - 5
x2 - 2x + 1 -6x + 12 = 3x - 5
x2 - 11x + 18 = 0 (product-som-methode met +18)
(x - 2)(x - 9) = 0
x - 2 = 0 v x - 9 = 0
x = 2 v x = 9
d.
(werk eerst de haakjes weg want er staat ... = 24 en niet ... = 0 )
x2 + 3x - 7x - 21 = 24
x2 - 4x - 45 = 0 (product-som-methode met -45)
(x + 5)(x - 9) = 0
x + 5 = 0 v x - 9 = 0
x = -5 v x = 9
e.
x2 - 2x - 16 = 5x - 16
x2 - 7x = 0 (haal x voor de haakjes)
x( x - 7) = 0
x = 0 v x - 7 = 0
x = 0 v x = 7
f.
x2 + 7x + 5x + 35 = x2 - 1 (de x2 valt links en rechts weg)
12x + 35 = -1
12x = -36
x = -3
20.
1/4x2 + 3½x + 12 = 0 (nu links en rechts maal 4)
x2 + 14x + 48 = 0 (product-som-methode met +48)
(x + 6)(x + 8) = 0
x + 6 = 0 v x + 8 = 0
x = -6 v x = -8
b.
-x2 + 6x - 5 = 0 (links en rechts maal -1)
x2 - 6x + 5 = 0 (product-som-methode met +5)
(x - 1)(x - 5) = 0
x - 1 = 0 v x - 5 = 0
x = 1 v x = 5
c.
-1/2x2 - 3x + 8 = 0 (links en rechts maal -2)
x2 + 6x - 16 = 0 (product-som-methode met -16)
(x - 2)(x + 8) = 0
x - 2 = 0 v x + 8 = 0
x = 2 v x = -8
d.
4x2 - 24x + 36 - x2 = 6x - 27
3x2 - 30x + 63 = 0 (links en rechts delen door 3)
x2 - 10x + 21 = 0 (product-som-methode met +21)
(x - 3)(x - 7) = 0
x - 3 = 0 v x - 7 = 0
x = 3 v x = 7
21.
100k2 - 4900k - 5000 = 0 (links en rechts :100)
k2 - 49k - 50 = 0 (product-som-methode met -50)
(k + 1)(k - 50) = 0
k + 1 = 0 v k - 50 = 0
k = -1 v k = 50
b.
(x - 2)(2x - 5) = x + 2
2x2 - 5x - 4x + 10 = x + 2
2x2 - 9x + 10 = x + 2
2x2 - 10x + 8 = 0 (links en rechts :2)
x2 - 5x + 4 = 0 (product-som-methode met +4)
(x - 1)(x - 4) = 0
x - 1 = 0 v x - 4 = 0
x = 1 v x = 4
c.
(x - 5)2 = 4 - 2(3 - x)
x2 - 10x + 25 = 4 - 6 + 2x
x2 - 10x + 25 = -2 + 2x
x2 - 12x + 27 = 0 (product-som-methode met +27)
(x - 3)(x - 9) = 0
x - 3 = 0 v x - 9 = 0
x = 3 v x = 9
d.
(2x - 1)(2x + 5) = 0
2x - 1 = 0 v 2x + 5 = 0
2x = 1 v 2x = -5
x = 1/2 v x = -5/2 = -2½
e.
(3x + 1)(x - 6) = 3x2
3x2 - 18x + x - 6 = 3x2 (links en rechts 3x2 wegstrepen)
-18x + x - 6 = 0
-17x = 6
x = -6/17
f.
-1/3x2 = x - 6 (links en rechts maal -3 om breuk weg te werken)
x2 = -3x + 18
x2 + 3x - 18 = 0 (product-som-methode met -18)
(x - 3)(x + 6) = 0
x - 3 = 0 v x + 6 = 0
x = 3 v x = -6
22.
x2 = 4x + 21
x2 - 4x - 21 = 0 (product-som-methode met -21)
(x + 3)(x - 7) = 0
x + 3 = 0 v x - 7 = 0
x = -3 v x = 7
b.
Hij had dus -3 of 7 in gedachten.
a. x(x + 6)
b. 5x(x - 4)
c. -x(x + 8)
d. x(x - 1)
14.
Tip:
Om te ontbinden in factoren maak je gebruik van de product-som-methode. Maak een T-tabel van de producten en sommen van het getal zonder de x. Vaak staat deze als laatste in een kwadratische vergelijking.
a. (x - 2)(x - 4)Om te ontbinden in factoren maak je gebruik van de product-som-methode. Maak een T-tabel van de producten en sommen van het getal zonder de x. Vaak staat deze als laatste in een kwadratische vergelijking.
b. (x + 2)(x + 7)
c. (x + 2)(x - 5) (zie afbeelding met een T-tabel van -10)
d. (x + 3)(x - 2)

15.
Tip:
Ontbinden in factoren wil zeggen, schrijf als: iets * iets = 0.
Omdat te laten kloppen dan moet of de ene 0 zijn, of de andere.
Meer wiskundig: Als A x B = 0 dan A = 0 of B = 0
a. x(3x - 5)Ontbinden in factoren wil zeggen, schrijf als: iets * iets = 0.
Omdat te laten kloppen dan moet of de ene 0 zijn, of de andere.
Meer wiskundig: Als A x B = 0 dan A = 0 of B = 0
b. (x + 1)(x - 2)
c. (x + 5)(x - 7)
d. a(a + 4)
e. (p + 1)(p + 14)
f. (q - 8)(q + 9)
16.
Tip:
Schrijf als het kan naar de vorm x2 + ax + b = 0
a. Schrijf als het kan naar de vorm x2 + ax + b = 0
x2 + 7x - 8 = 0 (product-som-methode met -8)
(x - 1)(x + 8) = 0
x - 1 = 0 v x + 8 = 0
x = 1 v x = -8
b.
2x2 - 6x = 0 (haal 2x voor de haakjes)
2x(x - 3) = 0
2x = 0 v x - 3 = 0
x = 0 v x = 3
c.
x2 - x = 0 (haal x voor de haakjes)
x(x - 1) = 0
x = 0 v x - 1 = 0
x = 0 v x = 1
d.
x2 - 6x + 5 = 0 (product-som-methode met 5)
(x - 1)(x - 5) = 0
x - 1 = 0 v x - 5 = 0
x = 1 v x = 5
e.
(is al ontbonden in factoren)
x - 1 = 0 v x + 3 = 0
x = 1 v x = -3
f.
x2 - 4x + 4 = 0 (product-som-methode met 4)
(x - 2)(x - 2) = 0
x - 2 = 0 v x - 2 = 0
x = 2 v x = 2
17.
Tip:
Vul de gevonden oplossing voor x (of a of p) maar eens in de vergelijking en zie dat het klopt.
Klopt het niet, dan heb je ergens een fout gemaakt.
Controle voor x = -2 bij a:
(-2)2 - 16 * -2 - 36 = 4 + 32 - 36 = 36 - 36 = 0, dus het is een goede oplossing.
a. Vul de gevonden oplossing voor x (of a of p) maar eens in de vergelijking en zie dat het klopt.
Klopt het niet, dan heb je ergens een fout gemaakt.
Controle voor x = -2 bij a:
(-2)2 - 16 * -2 - 36 = 4 + 32 - 36 = 36 - 36 = 0, dus het is een goede oplossing.
x2 - 16x - 36 = 0 (product-som-methode met -36)
(x + 2)(x - 18) = 0
x + 2 = 0 v x - 18 = 0
x = -2 v x = 18
b.
-p2 - 11p = 0 (links en rechts maal -1)
p2 + 11p = 0 (haal p voor de haakjes)
p(p + 11) = 0
p = 0 v p + 11 = 0
p = 0 v p = -11
c.
a2 - 18a + 45 = 0 (product-som-methode met 45)
(a - 3)(a - 15) = 0
a - 3 = 0 v a - 15 = 0
a = 3 v a = 15
18.
Tip:
c. is WEL van de vorm: A x B = 0
d. is NIET van de vorm: A x B = 0, want er staat in het begin ... = 10. Werk dus naar ... = 0.
a.c. is WEL van de vorm: A x B = 0
d. is NIET van de vorm: A x B = 0, want er staat in het begin ... = 10. Werk dus naar ... = 0.
x2 + x = 5x (links en rechts -5x)
x2 + x - 5x = 0
x2 - 4x = 0 (haal x voor de haakjes)
x(x - 4) = 0
x = 0 v x - 4 = 0
x = 0 v x = 4
b.
x2 + 6x + 9 = 2x + 9 (links en rechts -2x)
x2 + 6x - 2x + 9 = 9
x2 + 4x + 9 = 9 (links en rechts -9)
x2 + 4x = 0
x(x + 4) = 0
x = 0 v x + 4 = 0
x = 0 v x = -4
c.
(staat al goed ontbonden in factoren)
2t - 1 = 0 v t + 2 = 0
2t = 1 v t = -2
t = 1/2 v t = -2
d.
p2 + 2p - p - 2 = 10
p2 + p - 12 = 0 (product-som-methode met -12)
(p + 4)(p - 3) = 0 (nu is de vergelijking wel van de vorm A x B = 0)
p + 4 = 0 v p - 3 = 0
p = -4 v p = 3
19.
Tip:
Als de opgave in het begin niet goed ontbonden is in factoren (dus van de vorm A x B = 0), werk dan de haakjes weg en probeer het naar de vorm te schrijven:
x2 + ax + b = 0.
Gebruik daarna de product-som-methode of neem een factor van x voor de haakjes.
a.Als de opgave in het begin niet goed ontbonden is in factoren (dus van de vorm A x B = 0), werk dan de haakjes weg en probeer het naar de vorm te schrijven:
x2 + ax + b = 0.
Gebruik daarna de product-som-methode of neem een factor van x voor de haakjes.
(deze is al goed ontbonden in factoren, want is van de vorm: A x B = 0)
3x - 1 = 0 v 5x + 30 = 0
3x = 1 v 5x = -30
x = 1/3 v x = -6
b.
x2 - 10x + 25 = 2x - 10
x2 - 12x + 35 = 0 (product-som-methode met +35)
(x - 5)(x - 7) = 0
x - 5 = 0 v x - 7 = 0
x = 5 v x = 7
c.
x2 - 2x + 1 - 6(x - 2) = 3x - 5
x2 - 2x + 1 -6x + 12 = 3x - 5
x2 - 11x + 18 = 0 (product-som-methode met +18)
(x - 2)(x - 9) = 0
x - 2 = 0 v x - 9 = 0
x = 2 v x = 9
d.
(werk eerst de haakjes weg want er staat ... = 24 en niet ... = 0 )
x2 + 3x - 7x - 21 = 24
x2 - 4x - 45 = 0 (product-som-methode met -45)
(x + 5)(x - 9) = 0
x + 5 = 0 v x - 9 = 0
x = -5 v x = 9
e.
x2 - 2x - 16 = 5x - 16
x2 - 7x = 0 (haal x voor de haakjes)
x( x - 7) = 0
x = 0 v x - 7 = 0
x = 0 v x = 7
f.
x2 + 7x + 5x + 35 = x2 - 1 (de x2 valt links en rechts weg)
12x + 35 = -1
12x = -36
x = -3
20.
Tip:
Haal eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen (balansmethode).
a.Haal eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen (balansmethode).
1/4x2 + 3½x + 12 = 0 (nu links en rechts maal 4)
x2 + 14x + 48 = 0 (product-som-methode met +48)
(x + 6)(x + 8) = 0
x + 6 = 0 v x + 8 = 0
x = -6 v x = -8
b.
-x2 + 6x - 5 = 0 (links en rechts maal -1)
x2 - 6x + 5 = 0 (product-som-methode met +5)
(x - 1)(x - 5) = 0
x - 1 = 0 v x - 5 = 0
x = 1 v x = 5
c.
-1/2x2 - 3x + 8 = 0 (links en rechts maal -2)
x2 + 6x - 16 = 0 (product-som-methode met -16)
(x - 2)(x + 8) = 0
x - 2 = 0 v x + 8 = 0
x = 2 v x = -8
d.
4x2 - 24x + 36 - x2 = 6x - 27
3x2 - 30x + 63 = 0 (links en rechts delen door 3)
x2 - 10x + 21 = 0 (product-som-methode met +21)
(x - 3)(x - 7) = 0
x - 3 = 0 v x - 7 = 0
x = 3 v x = 7
21.
Tip:
Bij d: deze is al goed ontbonden in factoren, dus je kunt meteen gebruiken: Als A x B = 0 dan A = 0 of B = 0
a.Bij d: deze is al goed ontbonden in factoren, dus je kunt meteen gebruiken: Als A x B = 0 dan A = 0 of B = 0
100k2 - 4900k - 5000 = 0 (links en rechts :100)
k2 - 49k - 50 = 0 (product-som-methode met -50)
(k + 1)(k - 50) = 0
k + 1 = 0 v k - 50 = 0
k = -1 v k = 50
b.
(x - 2)(2x - 5) = x + 2
2x2 - 5x - 4x + 10 = x + 2
2x2 - 9x + 10 = x + 2
2x2 - 10x + 8 = 0 (links en rechts :2)
x2 - 5x + 4 = 0 (product-som-methode met +4)
(x - 1)(x - 4) = 0
x - 1 = 0 v x - 4 = 0
x = 1 v x = 4
c.
(x - 5)2 = 4 - 2(3 - x)
x2 - 10x + 25 = 4 - 6 + 2x
x2 - 10x + 25 = -2 + 2x
x2 - 12x + 27 = 0 (product-som-methode met +27)
(x - 3)(x - 9) = 0
x - 3 = 0 v x - 9 = 0
x = 3 v x = 9
d.
(2x - 1)(2x + 5) = 0
2x - 1 = 0 v 2x + 5 = 0
2x = 1 v 2x = -5
x = 1/2 v x = -5/2 = -2½
e.
(3x + 1)(x - 6) = 3x2
3x2 - 18x + x - 6 = 3x2 (links en rechts 3x2 wegstrepen)
-18x + x - 6 = 0
-17x = 6
x = -6/17
f.
-1/3x2 = x - 6 (links en rechts maal -3 om breuk weg te werken)
x2 = -3x + 18
x2 + 3x - 18 = 0 (product-som-methode met -18)
(x - 3)(x + 6) = 0
x - 3 = 0 v x + 6 = 0
x = 3 v x = -6
22.
Tip:
Stel een vergelijking op in x en los op.
a.Stel een vergelijking op in x en los op.
x2 = 4x + 21
x2 - 4x - 21 = 0 (product-som-methode met -21)
(x + 3)(x - 7) = 0
x + 3 = 0 v x - 7 = 0
x = -3 v x = 7
b.
Hij had dus -3 of 7 in gedachten.
23.
Omtrek hek = AB + BC + CD
32 = x + BC + x
32 = BC + 2x
BC + 2x = 32 (links en rechts -2x)
BC = 32 - 2x
b.
Oppervlakte = BC x CD
128 = (32 - 2x) ⋅ x
c.
Los op: 128 = (32 - 2x) ⋅ x
128 = 32x - 2x2 (zet x2 vooraan)
2x2 - 32x + 128 = 0 (links en rechts :2)
x2 - 16x + 64 = 0 (product-som-methode met +64)
(x - 8)(x - 8) = 0
x - 8 = 0 v x - 8 = 0
x = 8 v x = 8
Als x = 8 dan:
AB = x
BC = 32 - 2x
CD = x
Dus:
AB = 8
BC = 32 - 16 = 16
CD = 8
En dat klopt want 8 + 16 + 8 = 32 en dat is precies de gegeven omtrek.
24.
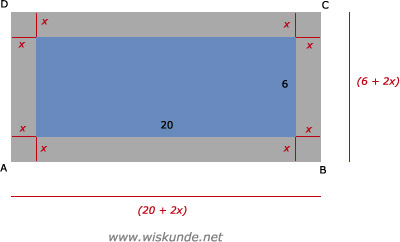
Oppervlakte tegelpad = (20 + 2x)(6 + 2x) - (20 ⋅ 6)
= (20 + 2x)(6 + 2x) - 120
= 120 + 40x + 12x + 4x2 - 120
= 4x2 + 52x
b.
Oppervlakte tegelpad = 4x2 + 52x
120 = 4x2 + 52x
Ofwel: 4x2 + 52x - 120 = 0
c.
Los op: 4x2 + 52x - 120 = 0 (links en rechts :4)
x2 + 13x - 30 = 0 (product-som-methode met -30)
(x - 2)(x + 15) = 0
x - 2 = 0 v x + 15 = 0
x = 2 v x = -15
Een negatieve afmeting van -15 kan niet dus we houden over x = 2.
Dus de breedte van het tegelpad is 2 meter.
25.
(3x - 1)2 - (2x + 1)2 = 5x + 20
9x2 - 6x + 1 - [4x2 + 4x + 1] = 5x + 20
9x2 - 6x + 1 - 4x2 - 4x - 1 = 5x + 20
5x2 - 15x - 20 = 0 (links en rechts :5)
x2 - 3x - 4 = 0 (product-som-methode met -4)
(x + 1)(x - 4) = 0
x + 1 = 0 v x - 4 = 0
x = -1 v x = 4
b.
x2 - 3[(x - 1)(x + 2)] = x
x2 - 3[x2 + 2x - x - 2] = x
x2 - 3[x2 + x - 2] = x
x2 - 3x2 - 3x + 6 = x
-2x2 - 4x + 6 = 0 (links en rechts :-2)
x2 + 2x - 3 = 0 (product-som-methode met -3)
(x - 1)(x + 3) = 0
x - 1 = 0 v x + 3 = 0
x = 1 v x = -3
26.
a.
(3x - 1)(4x - 1) = 0
x = 1/3 v x = 1/4
b.
(2x + 1)(4x + 1) = 0
x = -1/2 v x = -1/4
c.
(5x - 1)(4x + 1) = 0
x = 1/5 v x = -1/4
d.
(3x - 1)(2x - 5) = 0
x = 1/3 v x = 2 1/2
e.
(x + 2)(x - 1/2) = 0
x = -2 v x = 1/2
f.
(x - 3)(x - 1/3) = 0
x = 3 v x = 1/3
g.
(3x - 1)(6x + 5) = 0
x = 1/3 v x = -5/6
Tip:
Omtrek hek = AB + BC + CD en vul in wat je weet.
Oppervlakte = lengte x breedte = BC x CD en vul ook hier in wat je weet.
a.Omtrek hek = AB + BC + CD en vul in wat je weet.
Oppervlakte = lengte x breedte = BC x CD en vul ook hier in wat je weet.
Omtrek hek = AB + BC + CD
32 = x + BC + x
32 = BC + 2x
BC + 2x = 32 (links en rechts -2x)
BC = 32 - 2x
b.
Oppervlakte = BC x CD
128 = (32 - 2x) ⋅ x
c.
Los op: 128 = (32 - 2x) ⋅ x
128 = 32x - 2x2 (zet x2 vooraan)
2x2 - 32x + 128 = 0 (links en rechts :2)
x2 - 16x + 64 = 0 (product-som-methode met +64)
(x - 8)(x - 8) = 0
x - 8 = 0 v x - 8 = 0
x = 8 v x = 8
Als x = 8 dan:
AB = x
BC = 32 - 2x
CD = x
Dus:
AB = 8
BC = 32 - 16 = 16
CD = 8
En dat klopt want 8 + 16 + 8 = 32 en dat is precies de gegeven omtrek.
24.
Tip:
Oppervlakte tegelpad (grijs) = oppervlakte(ABCD) - oppervlakte(zwembad-blauw)
a.Oppervlakte tegelpad (grijs) = oppervlakte(ABCD) - oppervlakte(zwembad-blauw)
Oppervlakte tegelpad = (20 + 2x)(6 + 2x) - (20 ⋅ 6)
= (20 + 2x)(6 + 2x) - 120
= 120 + 40x + 12x + 4x2 - 120
= 4x2 + 52x
b.
Oppervlakte tegelpad = 4x2 + 52x
120 = 4x2 + 52x
Ofwel: 4x2 + 52x - 120 = 0
c.
Los op: 4x2 + 52x - 120 = 0 (links en rechts :4)
x2 + 13x - 30 = 0 (product-som-methode met -30)
(x - 2)(x + 15) = 0
x - 2 = 0 v x + 15 = 0
x = 2 v x = -15
Een negatieve afmeting van -15 kan niet dus we houden over x = 2.
Dus de breedte van het tegelpad is 2 meter.

25.
Tip:
Let op de rode haken. Werk eerst uit wat binnen de rode haken staat en verwerk dan wat er nog voor staat!
a.Let op de rode haken. Werk eerst uit wat binnen de rode haken staat en verwerk dan wat er nog voor staat!
(3x - 1)2 - (2x + 1)2 = 5x + 20
9x2 - 6x + 1 - [4x2 + 4x + 1] = 5x + 20
9x2 - 6x + 1 - 4x2 - 4x - 1 = 5x + 20
5x2 - 15x - 20 = 0 (links en rechts :5)
x2 - 3x - 4 = 0 (product-som-methode met -4)
(x + 1)(x - 4) = 0
x + 1 = 0 v x - 4 = 0
x = -1 v x = 4
b.
x2 - 3[(x - 1)(x + 2)] = x
x2 - 3[x2 + 2x - x - 2] = x
x2 - 3[x2 + x - 2] = x
x2 - 3x2 - 3x + 6 = x
-2x2 - 4x + 6 = 0 (links en rechts :-2)
x2 + 2x - 3 = 0 (product-som-methode met -3)
(x - 1)(x + 3) = 0
x - 1 = 0 v x + 3 = 0
x = 1 v x = -3
26.
a.
(3x - 1)(4x - 1) = 0
x = 1/3 v x = 1/4
b.
(2x + 1)(4x + 1) = 0
x = -1/2 v x = -1/4
c.
(5x - 1)(4x + 1) = 0
x = 1/5 v x = -1/4
d.
(3x - 1)(2x - 5) = 0
x = 1/3 v x = 2 1/2
e.
(x + 2)(x - 1/2) = 0
x = -2 v x = 1/2
f.
(x - 3)(x - 1/3) = 0
x = 3 v x = 1/3
g.
(3x - 1)(6x + 5) = 0
x = 1/3 v x = -5/6
Andere paragrafen:
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
3.1. Kwadratische functies (1 t/m 12)
3.2. Kwadratische vergelijkingen (13 t/m 26)
3.3. Snijpunten van grafieken (27 t/m 35)
3.4. De abc-formule (36 t/m 52)
3.5. Verschillende oplossingsmethoden (53 t/m 60)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


