TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.5 Lijnstukken berekenen VWO 3
Boek: Getal & Ruimte - Goniometrie VWO 3 (deel 2) opgaven 50 t/m 62, 2011Je kunt lijnstukken ook berekenen met snavel- en zandloperfiguren. Gebruik hierbij ook F-hoeken en Z-hoeken.
Soms moet je een lijnstuk gelijk stellen aan x.
De oppervlakte in een driehoek kun je vaak op meerdere manieren berekenen.
Je hebt namelijk 3 zijden en dus ook 3 bijbehorende hoogtes.
Met de zijde x hoogte-methode kun je zo ook lijnstukken berekenen.
Soms moet je een lijnstuk gelijk stellen aan x.
De oppervlakte in een driehoek kun je vaak op meerdere manieren berekenen.
Je hebt namelijk 3 zijden en dus ook 3 bijbehorende hoogtes.
Met de zijde x hoogte-methode kun je zo ook lijnstukken berekenen.
50.
BC2 = AC2 + AB2
BC2 = 32 + 22
BC2 = 9 + 4
BC2 = 13
BC = √13
BC ≈ 3,61
b.
cos(∠L) = A/S = KL/LM
cos(58º) = 2/LM
LM = 2 / cos(58º)
LM ≈ 3,77
c.
1½ ⋅ QR = 2 ⋅ 3
QR = 6 / 1,5
QR = 4
51.
2 ⋅ (x + 6) = 5 ⋅ x (kruislings vermenigvuldigen)
2x + 12 = 5x
-3x + 12 = 0
-3x = -12
x = -12/-3 = 4
Dus BD = 4, en AB = (x + 6) = 4 + 6 = 10
52.
8,1 ⋅ x = 6,0 ⋅ (x + 2,3) (kruislings vermenigvuldigen)
8,1x = 6,0x + 13,8
2,1x = 13,8
x = 13,8 / 2,1
x ≈ 6,57
Dus AK = x = 6,57
b.
8,1 ⋅ (y + 8,87) = 8,87 ⋅ 9,6 (kruislings vermenigvuldigen)
8,1y + 71,847 = 85,152
8,1y = 13,305
y = 13,305 / 8,1 = 1,6425
Dus BM = y ≈ 1,6
53.
1,5 ⋅ (x + 3) = 6 ⋅ x
1,5x + 4,5 = 6x
-4,5x = -4,5
x = -4,5 / -4,5
x = 1
Dus DP = 1
b.
tan(∠S) = O/A = AP/AS = (AD + DP)/AS = (3 + 1)/6 = 4/6
∠S = tan-1(4/6)
∠S ≈ 33,7º
c.
QC = 4 - 1,5 = 2,5
1,5 ⋅ CR = 1 ⋅ 2,5
1,5CR = 2,5
CR = 2,5 / 1,5
CR ≈ 1,67
Bereken nu QR met de stelling van Pythagoras:
QR2 = CR2 + CQ2
QR2 = 1,672 + 2,52
QR2 = 9,0389
QR = √9,0389
QR ≈ 3,0
54.
x ⋅ (x + 18) = 18 ⋅ 8
x2 + 18x = 144
x2 + 18x - 144 = 0
(x - 6)(x + 24) = 0
x - 6 = 0 v x + 24 = 0
x = 6 v x = -24 (kan niet)
Dus DE = x = 6

55.
PR2 = PS2 + RS2
PR2 = 10,82 + 14,42
PR2 = 324
PR = √324
PR = 18
b.
14,4 ⋅ x = 8,1 ⋅ (18 - x)
14,4x = 145,8 - 8,1x
22,5x = 145,8
x = 145,8 / 22,5
x = 6,48
Dus PV = 6,48
c.
14,4 ⋅ x = 4,5 ⋅ (18 - x)
14,4x = 81 - 4,5x
18,9x = 81
x = 81 / 18,9
x ≈ 4,29
Dus RW = x = 4,29
VW = PR - PV - RW
VW = 18 - 6,48 - 4,29
VW = 7,23
56.
b. AB x AC = 16 x 12 = 192
BC x AD = (12,8 + 7,2) x 9,6 = 192
Je ziet dat ze gelijk zijn.
57.
BC2 = 42 + 22
BC2 = 20
BC = √20
BC ≈ 4,47
Zijde x hoogte-methode:
AB x AC = BC x AD
4 x 2 = √20 x AD
8 = √20 x AD
AD = 8 / √20
AD ≈ 1,8
58.
CD2 + 52 = 132
CD2 = 169 - 25
CD2 = 144
CD = √144
CD = 12
Zijde x hoogte-methode:
AC x BE = AB x CD
13 x BE = 10 x 12
13BE = 120
BE = 120 / 13
BE ≈ 9,2
59.
HB2 = 12 + 72
HB2 = 50
HB = √50
HB ≈ 7,07
Zijde x hoogte-methode:
BH x CK = BC x EH
√50 x CK = 4 x 7
√50 x CK = 28
CK = 28 / √50
CK ≈ 3,96
Tip:
Bij a: bereken met de Stelling van Pythagoras
Bij b: bereken met SOS CAS TOA
Bij c: bereken met gelijkvormigheid
a.Bij a: bereken met de Stelling van Pythagoras
Bij b: bereken met SOS CAS TOA
Bij c: bereken met gelijkvormigheid
BC2 = AC2 + AB2
BC2 = 32 + 22
BC2 = 9 + 4
BC2 = 13
BC = √13
BC ≈ 3,61
b.
cos(∠L) = A/S = KL/LM
cos(58º) = 2/LM
LM = 2 / cos(58º)
LM ≈ 3,77
c.
| RT | TS | SR | RT | 1,5 | 3 | |
| RP | PQ | QR | => | RP | 2 | QR |
1½ ⋅ QR = 2 ⋅ 3
QR = 6 / 1,5
QR = 4
51.
Tip:
Zet de 2 gelijkvormige driehoeken even als losse schets naast elkaar. Dan zie je het beter.
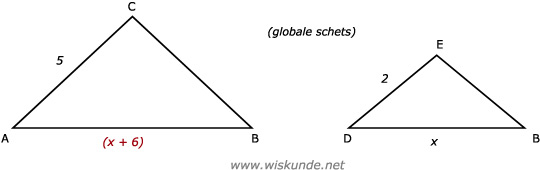
Stel BD = x dan AB = (x + 6)
Zet de 2 gelijkvormige driehoeken even als losse schets naast elkaar. Dan zie je het beter.
Stel BD = x dan AB = (x + 6)
| AB | BC | AC | (x + 6) | BC | 5 | |
| BD | BE | DE | => | x | BE | 2 |
2 ⋅ (x + 6) = 5 ⋅ x (kruislings vermenigvuldigen)
2x + 12 = 5x
-3x + 12 = 0
-3x = -12
x = -12/-3 = 4
Dus BD = 4, en AB = (x + 6) = 4 + 6 = 10

52.
Tip:
Bij a: Stel AK = x
Bij b: Stel BM = y, dan AM = AK + 2,3 = 6,57 + 2,3 = 8,87
a.Bij a: Stel AK = x
Bij b: Stel BM = y, dan AM = AK + 2,3 = 6,57 + 2,3 = 8,87
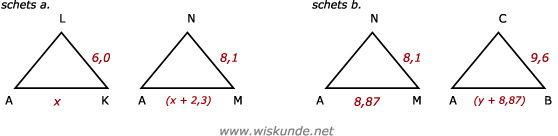
| AK | KL | AL | x | 6,0 | AL | |
| AM | MN | AN | => | (x + 2,3) | 8,1 | AN |
8,1 ⋅ x = 6,0 ⋅ (x + 2,3) (kruislings vermenigvuldigen)
8,1x = 6,0x + 13,8
2,1x = 13,8
x = 13,8 / 2,1
x ≈ 6,57
Dus AK = x = 6,57
b.
| AM | MN | AN | 8,87 | 8,1 | AN | |
| AB | BC | AC | => | (y + 8,87) | 9,6 | AC |
8,1 ⋅ (y + 8,87) = 8,87 ⋅ 9,6 (kruislings vermenigvuldigen)
8,1y + 71,847 = 85,152
8,1y = 13,305
y = 13,305 / 8,1 = 1,6425
Dus BM = y ≈ 1,6

53.
Tip:
Bij a: Stel DP = x
Bij c: Gebruik zandloperfiguur PDQ-QCR
a.Bij a: Stel DP = x
Bij c: Gebruik zandloperfiguur PDQ-QCR
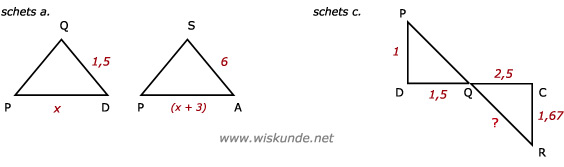
| PD | DQ | PQ | x | 1,5 | PQ | |
| AP | AS | PS | => | (x + 3) | 6 | PS |
1,5x + 4,5 = 6x
-4,5x = -4,5
x = -4,5 / -4,5
x = 1
Dus DP = 1
b.
tan(∠S) = O/A = AP/AS = (AD + DP)/AS = (3 + 1)/6 = 4/6
∠S = tan-1(4/6)
∠S ≈ 33,7º
c.
QC = 4 - 1,5 = 2,5
| DQ | PQ | DP | 1,5 | PQ | 1 | |
| CQ | QR | CR | => | 2,5 | QR | CR |
1,5 ⋅ CR = 1 ⋅ 2,5
1,5CR = 2,5
CR = 2,5 / 1,5
CR ≈ 1,67
Bereken nu QR met de stelling van Pythagoras:
QR2 = CR2 + CQ2
QR2 = 1,672 + 2,52
QR2 = 9,0389
QR = √9,0389
QR ≈ 3,0

54.
Tip:
Stel DE = x dan BD is ook x.
Stel DE = x dan BD is ook x.
| AD | DE | AE | 18 | x | AE | |
| AB | BC | AC | => | (x + 18) | 8 | AC |
x2 + 18x = 144
x2 + 18x - 144 = 0
(x - 6)(x + 24) = 0
x - 6 = 0 v x + 24 = 0
x = 6 v x = -24 (kan niet)
Dus DE = x = 6

55.
Tip:
Bij a: PR kan met de stelling van Pythagoras
Bij b: Stel PV = x en gebruik dan de zandloperfiguur
Bij c: Stel RW = x. Dan PW = 18 - x (zandloper)
a.Bij a: PR kan met de stelling van Pythagoras
Bij b: Stel PV = x en gebruik dan de zandloperfiguur
Bij c: Stel RW = x. Dan PW = 18 - x (zandloper)
PR2 = PS2 + RS2
PR2 = 10,82 + 14,42
PR2 = 324
PR = √324
PR = 18
b.
14,4 ⋅ x = 8,1 ⋅ (18 - x)
14,4x = 145,8 - 8,1x
22,5x = 145,8
x = 145,8 / 22,5
x = 6,48
Dus PV = 6,48
c.
14,4 ⋅ x = 4,5 ⋅ (18 - x)
14,4x = 81 - 4,5x
18,9x = 81
x = 81 / 18,9
x ≈ 4,29
Dus RW = x = 4,29
VW = PR - PV - RW
VW = 18 - 6,48 - 4,29
VW = 7,23
56.
Tip:
De oppervlakte van driehoek ABC (½ x basis x hoogte) kan op 2 manieren:
opp(ABC) = ½ x AB x AC
opp(ABC) = ½ x BC x AD
a. AB = √256 = 16 en AC = √144 = 12 (met de stelling van Pythagoras) De oppervlakte van driehoek ABC (½ x basis x hoogte) kan op 2 manieren:
opp(ABC) = ½ x AB x AC
opp(ABC) = ½ x BC x AD
b. AB x AC = 16 x 12 = 192
BC x AD = (12,8 + 7,2) x 9,6 = 192
Je ziet dat ze gelijk zijn.
57.
Tip:
Bereken eerst BC met de stelling van Pythagoras en gebruik dan de zijde x hoogte-methode.
BC2 = AB2 + AC2Bereken eerst BC met de stelling van Pythagoras en gebruik dan de zijde x hoogte-methode.
BC2 = 42 + 22
BC2 = 20
BC = √20
BC ≈ 4,47
Zijde x hoogte-methode:
AB x AC = BC x AD
4 x 2 = √20 x AD
8 = √20 x AD
AD = 8 / √20
AD ≈ 1,8
58.
Tip:
Bereken eerst CD met de stelling van Pythagoras en gebruik dan de zijde x hoogte-methode.
CD2 + BD2 = BC2Bereken eerst CD met de stelling van Pythagoras en gebruik dan de zijde x hoogte-methode.
CD2 + 52 = 132
CD2 = 169 - 25
CD2 = 144
CD = √144
CD = 12
Zijde x hoogte-methode:
AC x BE = AB x CD
13 x BE = 10 x 12
13BE = 120
BE = 120 / 13
BE ≈ 9,2
59.
Tip:
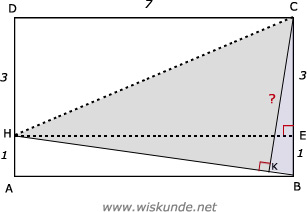
Trek 2 hulplijnen: HC en HE en gebruik driehoek HBC.
Bereken HB met de stelling van Pythagoras.
Gebruik dan de zijde x hoogte-methode.
HB2 = AH2 + AB2Trek 2 hulplijnen: HC en HE en gebruik driehoek HBC.
Bereken HB met de stelling van Pythagoras.
Gebruik dan de zijde x hoogte-methode.
HB2 = 12 + 72
HB2 = 50
HB = √50
HB ≈ 7,07
Zijde x hoogte-methode:
BH x CK = BC x EH
√50 x CK = 4 x 7
√50 x CK = 28
CK = 28 / √50
CK ≈ 3,96

60.
CD2 = 122 + 42
CD2 = 160
CD = √160
CD ≈ 12,5
Zijde x hoogte-methode:
BC x DF = CD x BE
9 x 12 = √160 x BE
108 = √160 x BE
BE = 108 / √160
BE ≈ 8,54
61.
BD2 = 82 + 62
BD2 = 64 + 36 = 100
BD = √100
BD = 10
DF2 = BD2 + BF2
DF2 = 102 + 52
DF2 = 125
DF = √125
DF ≈ 11,2
Zijde x hoogte-methode:
DF x HP = HD x FH
√125 x HP = 5 x 10
HP = 50 / √125
HP ≈ 4,47
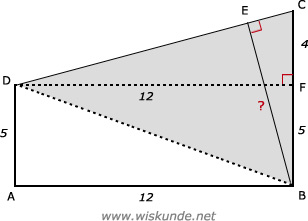
62.
16,92 = 6,52 + CM2
CM2 = 243,36
CM = √243,36
CM ≈ 15,6
Zijde x hoogte-methode in driehoek ABC:
AB x CM = BC x AP
13 x √243,36 = 16,9 x AP
AP = ( 13 x √243,36 ) / 16,9
AP = 12
Dus 1 kabel is gelijk aan 12 meter.
Er zijn 216 x 2 = 432 kabels aangebracht.
Totale lengte is dus 432 x 12 = 5184 meter.
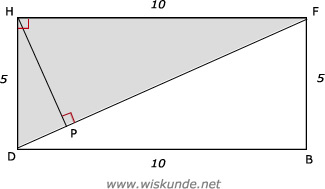
Tip:
Trek 2 hulplijnen: BD en DF en gebruik driehoek BCD.
Bereken CD met de stelling van Pythagoras.
Gebruik dan de zijde x hoogte-methode.
CD2 = DF2 + CF2Trek 2 hulplijnen: BD en DF en gebruik driehoek BCD.
Bereken CD met de stelling van Pythagoras.
Gebruik dan de zijde x hoogte-methode.
CD2 = 122 + 42
CD2 = 160
CD = √160
CD ≈ 12,5
Zijde x hoogte-methode:
BC x DF = CD x BE
9 x 12 = √160 x BE
108 = √160 x BE
BE = 108 / √160
BE ≈ 8,54

61.
Tip:
Maak een schets van diagonaalvlak DBFH.
Bereken dan eerst BD met de stelling van Pythagoras.
Bereken dan DF met de stelling van Pythagoras.
Gebruik dan de zijde x hoogte-methode in driehoek DFH.
BD2 = AB2 + AD2Maak een schets van diagonaalvlak DBFH.
Bereken dan eerst BD met de stelling van Pythagoras.
Bereken dan DF met de stelling van Pythagoras.
Gebruik dan de zijde x hoogte-methode in driehoek DFH.
BD2 = 82 + 62
BD2 = 64 + 36 = 100
BD = √100
BD = 10
DF2 = BD2 + BF2
DF2 = 102 + 52
DF2 = 125
DF = √125
DF ≈ 11,2
Zijde x hoogte-methode:
DF x HP = HD x FH
√125 x HP = 5 x 10
HP = 50 / √125
HP ≈ 4,47

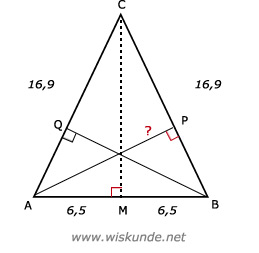
62.
Tip:
Trek CM loodrecht op AB.
AP is de lengte van 1 kabel. Bereken dus eerst AP.
AC2 = AM2 + CM2Trek CM loodrecht op AB.
AP is de lengte van 1 kabel. Bereken dus eerst AP.
16,92 = 6,52 + CM2
CM2 = 243,36
CM = √243,36
CM ≈ 15,6
Zijde x hoogte-methode in driehoek ABC:
AB x CM = BC x AP
13 x √243,36 = 16,9 x AP
AP = ( 13 x √243,36 ) / 16,9
AP = 12
Dus 1 kabel is gelijk aan 12 meter.
Er zijn 216 x 2 = 432 kabels aangebracht.
Totale lengte is dus 432 x 12 = 5184 meter.

Andere paragrafen:
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


