TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.4 Berekeningen in de ruimte VWO 3
Boek: Getal & Ruimte - Goniometrie VWO 3 (deel 2) opgaven 39 t/m 49, 2011Welke hoeken in een balk of kubus zijn recht?
Bij een balk (en kubus) zijn de hoeken in een zijvlak of diagonaalvlak 90º.
Omdat de hoeken recht zijn, kunnen we gebruik maken van de Stelling van Pythagoras en goniometrische verhoudingen.
Bij een balk (en kubus) zijn de hoeken in een zijvlak of diagonaalvlak 90º.
Omdat de hoeken recht zijn, kunnen we gebruik maken van de Stelling van Pythagoras en goniometrische verhoudingen.
39.
b. ∠B1 = ∠ABS
c. ∠B2 = ∠CBS
d. ∠S3 = ∠BSC
e. ∠C2 = ∠DCS
f. ∠D1 = ∠ADS
40.
Dus ∠BAG is groter dan 45º.
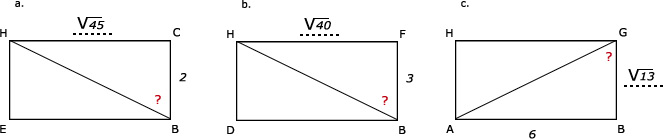
41.
∠CBH ligt in diagonaalvlak: EBCH
Bereken eerst CH en gebruik dan de tangens.
CH2 = CG2 + GH2
CH2 = 32 + 62
CH2 = 45
CH = √45
CH ≈ 6,7
tan(∠CBH) = O/A = CH/BC = √45 / 2
∠CBH = tan-1( √45 / 2 )
∠CBH ≈ 73,40º
b.
∠HBF ligt in diagonaalvlak: DBFH
Bereken eerst HF en gebruik dan de tangens.
HF2 = FG2 + GH2
HF2 = 22 + 62
HF2 = 40
HF = √40
HF ≈ 6,32
tan(∠HBF) = O/A = FH/BF = √40 / 3
∠HBF = tan-1( √40 / 3 )
∠HBF ≈ 64,62º
c.
∠AGB ligt in diagonaalvlak: ABGH
Bereken eerst BG en gebruik dan de tangens.
BG2 = BC2 + CG2
BG2 = 22 + 32
BG2 = 13
BG = √13
BG ≈ 3,6
tan(∠AGB) = O/A = AB/BG = 6 / √13
∠AGB = tan-1( 6 / √13 )
∠AGB ≈ 59,00º
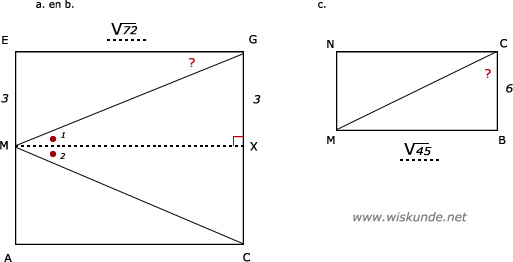
42.
∠EGM ligt in (diagonaal)vlak: EGXM
Bereken eerst EG en gebruik dan de tangens.
EG2 = EH2 + GH2
EG2 = 62 + 62
EG2 = 72
EG = √72
EG ≈ 8,5
tan(∠EGM) = O/A = EM/EG = 3 / √72
∠EGM = tan-1( 3 / √72 )
∠EGM ≈ 19,47º
b.
∠CMG ligt in diagonaalvlak: ACGE
Trek lijn MX. Dit is de symmetrie-as van driehoek CMG.
Hieruit volgt: ∠M1 = ∠M2
Op basis van Z-hoeken geldt: ∠EGM = ∠M1
Dus ∠CMG = 2 x ∠M1 = 2 x ∠EGM
Dus ∠CMG = 2 x 19,47º = 38,94º
c.
BM2 = AB2 + AM2
BM2 = 62 + 32
BM2 = 45
BM = √45
BM ≈ 6,7
tan(∠MCB) = O/A = BM/BC = √45 / 6
∠MCB = tan-1( √45 / 6 )
∠MCB ≈ 48,19º
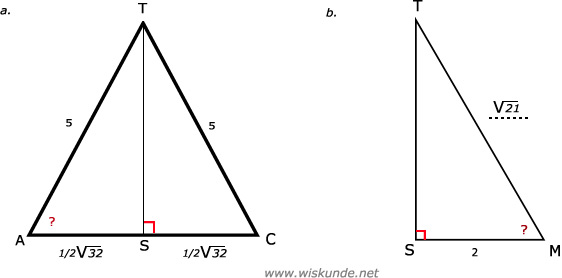
43.
AC2 = AB2 + BC2
AC2 = 42 + 42
AC2 = 32
AC = √32 (laat de wortel maar staan)
cos(∠A) = A/S = AS/AT = ½√32 / 5
∠A = ∠TAS = cos-1( ½√32 / 5 )
∠A = ∠TAS ≈ 55,6º
b.
BT2 = BM2 + MT2
52 = 22 + MT2
MT2 = 21
MT = √21 (laat de wortel maar staan)
cos(∠M) = A/S = MS/MT = 2 / √21
∠M = ∠TMS = cos-1( 2 / √21 )
∠M = ∠TMS ≈ 64,1º
44.
AC2 = AB2 + BC2
AC2 = 36 + 64 = 100
AC = √100
AC = 10
AS = 0,5 x 10 = 5
AT2 = AS2 + ST2
132 = 52 + ST2
ST2 = 144
ST = √144 = 12
b.
AT2 = AM2 + MT2
132 = 32 + MT2
MT2 = 160
MT = √160
MT ≈ 12,65
c.
In driehoek MST geldt: ∠TMS = tan-1(12/4) ≈ 71,6º
In driehoek NST geldt: ∠TNS = tan-1(12/3) ≈ 76,0º
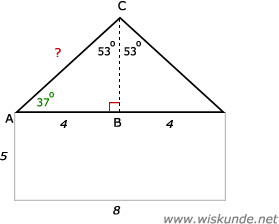
45.
cos(∠A) = A/S = AB/AC
cos(37º) = 4/AC
AC = 4 / cos(37º)
AC ≈ 5,01 (meter)
Oppervlakte dak: lengte x breedte = l x b = 5,01 x 12 x 2 = 120,24 m2
Kosten dakdekking: 120,24 x 115 = 13 827,60 euro
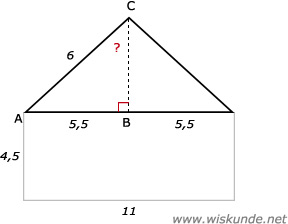
46.
Dus 1 dakdeel is 54 m2.
Oppervlakte dakdeel (rechthoek) = lengte x breedte = 54
Dus: lengte x 9 = 54
Dus de schuine AC is gelijk aan 6 m2
sin(∠C) = O/S = AB/AC = 5,5/6
∠C = sin-1(5,5 / 6)
∠C ≈ 66,44º
Dus de gevraagde hoek is 2 x 66,44º = 132,88º.
47.
In driehoek BCF geldt:
CF2 = BC2 + BF2
CF2 = 62 + 42
CF2 = 52
CF = √52
tan(∠CEF) = O/A = CF/EF = √52 / 6
∠CEF = tan-1( √52 / 6 )
∠CEF ≈ 50,24º
b.
Via Pythagoras zien we dat AF = FC = √52.
Dus driehoek ACF is gelijkbenig.
c.
In driehoek ABC geldt: AC = √72 (Pythagoras)
cos(∠MCF) = A/S = CM/CF
cos(∠MCF) = ½√72 / √52
∠MCF = cos-1( ½√72 / √52 )
∠MCF ≈ 53,96º
Dus ∠ACF = ∠MCF = 54º
48.
a. ∠DME ≈ 45,2º
b. ∠CMF ≈ 42,7º
c. ∠MPN ≈ 48,7º
Tip:
We kunnen hoeken ook weergeven met 3 letters.
De middelste letter is het hoekpunt.
a. ∠A2 = ∠DAS We kunnen hoeken ook weergeven met 3 letters.
De middelste letter is het hoekpunt.
b. ∠B1 = ∠ABS
c. ∠B2 = ∠CBS
d. ∠S3 = ∠BSC
e. ∠C2 = ∠DCS
f. ∠D1 = ∠ADS
40.
Tip:
Bereken BG. Is deze langer dan 5 dan is ∠BAG groter dan 45º.
BG = √50 ≈ 7,07Bereken BG. Is deze langer dan 5 dan is ∠BAG groter dan 45º.
Dus ∠BAG is groter dan 45º.
41.
Tip:
Maak eerst een schets van het juiste diagonaalvlak. Bereken dan de ontbrekende zijde met Pythagoras. Bereken daarna de hoek met de tangens.
a.Maak eerst een schets van het juiste diagonaalvlak. Bereken dan de ontbrekende zijde met Pythagoras. Bereken daarna de hoek met de tangens.
∠CBH ligt in diagonaalvlak: EBCH
Bereken eerst CH en gebruik dan de tangens.
CH2 = CG2 + GH2
CH2 = 32 + 62
CH2 = 45
CH = √45
CH ≈ 6,7
tan(∠CBH) = O/A = CH/BC = √45 / 2
∠CBH = tan-1( √45 / 2 )
∠CBH ≈ 73,40º
b.
∠HBF ligt in diagonaalvlak: DBFH
Bereken eerst HF en gebruik dan de tangens.
HF2 = FG2 + GH2
HF2 = 22 + 62
HF2 = 40
HF = √40
HF ≈ 6,32
tan(∠HBF) = O/A = FH/BF = √40 / 3
∠HBF = tan-1( √40 / 3 )
∠HBF ≈ 64,62º
c.
∠AGB ligt in diagonaalvlak: ABGH
Bereken eerst BG en gebruik dan de tangens.
BG2 = BC2 + CG2
BG2 = 22 + 32
BG2 = 13
BG = √13
BG ≈ 3,6
tan(∠AGB) = O/A = AB/BG = 6 / √13
∠AGB = tan-1( 6 / √13 )
∠AGB ≈ 59,00º

42.
Tip:
Bij a. en b.: Maak een schets van diagonaalvlak ACGE en trek de loodlijn MX op CG.
a.Bij a. en b.: Maak een schets van diagonaalvlak ACGE en trek de loodlijn MX op CG.
∠EGM ligt in (diagonaal)vlak: EGXM
Bereken eerst EG en gebruik dan de tangens.
EG2 = EH2 + GH2
EG2 = 62 + 62
EG2 = 72
EG = √72
EG ≈ 8,5
tan(∠EGM) = O/A = EM/EG = 3 / √72
∠EGM = tan-1( 3 / √72 )
∠EGM ≈ 19,47º
b.
∠CMG ligt in diagonaalvlak: ACGE
Trek lijn MX. Dit is de symmetrie-as van driehoek CMG.
Hieruit volgt: ∠M1 = ∠M2
Op basis van Z-hoeken geldt: ∠EGM = ∠M1
Dus ∠CMG = 2 x ∠M1 = 2 x ∠EGM
Dus ∠CMG = 2 x 19,47º = 38,94º
c.
BM2 = AB2 + AM2
BM2 = 62 + 32
BM2 = 45
BM = √45
BM ≈ 6,7
tan(∠MCB) = O/A = BM/BC = √45 / 6
∠MCB = tan-1( √45 / 6 )
∠MCB ≈ 48,19º

43.
Tip:
Bij a: Maak een schets van driehoek ACT en bereken met Pythagoras AC. Dan AS = 1/2 AC. Bereken daarna de hoek.
Bij b: Maak een schets van driehoek TSM en bereken met Pythagoras MT. Bereken daarna de hoek.
a.Bij a: Maak een schets van driehoek ACT en bereken met Pythagoras AC. Dan AS = 1/2 AC. Bereken daarna de hoek.
Bij b: Maak een schets van driehoek TSM en bereken met Pythagoras MT. Bereken daarna de hoek.
AC2 = AB2 + BC2
AC2 = 42 + 42
AC2 = 32
AC = √32 (laat de wortel maar staan)
cos(∠A) = A/S = AS/AT = ½√32 / 5
∠A = ∠TAS = cos-1( ½√32 / 5 )
∠A = ∠TAS ≈ 55,6º
b.
BT2 = BM2 + MT2
52 = 22 + MT2
MT2 = 21
MT = √21 (laat de wortel maar staan)
cos(∠M) = A/S = MS/MT = 2 / √21
∠M = ∠TMS = cos-1( 2 / √21 )
∠M = ∠TMS ≈ 64,1º

44.
Tip:
Bij a: Gebruik de stelling van Pythagoras. Zie dat AS = 1/2 AC en ∠AST = 90º.
Bij b: Gebruik driehoek ATM
Bij c: MS = BN = 4 en NS = BM = 3
a.Bij a: Gebruik de stelling van Pythagoras. Zie dat AS = 1/2 AC en ∠AST = 90º.
Bij b: Gebruik driehoek ATM
Bij c: MS = BN = 4 en NS = BM = 3
AC2 = AB2 + BC2
AC2 = 36 + 64 = 100
AC = √100
AC = 10
AS = 0,5 x 10 = 5
AT2 = AS2 + ST2
132 = 52 + ST2
ST2 = 144
ST = √144 = 12
b.
AT2 = AM2 + MT2
132 = 32 + MT2
MT2 = 160
MT = √160
MT ≈ 12,65
c.
In driehoek MST geldt: ∠TMS = tan-1(12/4) ≈ 71,6º
In driehoek NST geldt: ∠TNS = tan-1(12/3) ≈ 76,0º
45.
Tip:
Bereken eerst AC. Bereken dan de oppervlakte van het dak.
(AC x 12) x 2 dakdelen
∠A = 180º - 90º - 53º = 37ºBereken eerst AC. Bereken dan de oppervlakte van het dak.
(AC x 12) x 2 dakdelen
cos(∠A) = A/S = AB/AC
cos(37º) = 4/AC
AC = 4 / cos(37º)
AC ≈ 5,01 (meter)
Oppervlakte dak: lengte x breedte = l x b = 5,01 x 12 x 2 = 120,24 m2
Kosten dakdekking: 120,24 x 115 = 13 827,60 euro

46.
Tip:
Zie schets. Bereken eerst AC. Bereken dan de sinus van hoek C.
Oppervlakte 2 dakdelen samen is 108 m2.Zie schets. Bereken eerst AC. Bereken dan de sinus van hoek C.
Dus 1 dakdeel is 54 m2.
Oppervlakte dakdeel (rechthoek) = lengte x breedte = 54
Dus: lengte x 9 = 54
Dus de schuine AC is gelijk aan 6 m2
sin(∠C) = O/S = AB/AC = 5,5/6
∠C = sin-1(5,5 / 6)
∠C ≈ 66,44º
Dus de gevraagde hoek is 2 x 66,44º = 132,88º.

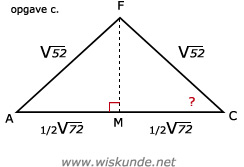
47.
Tip:
Bij a: ∠EFC is gelijk aan 90º
Bij c: Maak een goede schets van driehoek AFC en verwerk de gegevens uit opgave a. en b.
a.Bij a: ∠EFC is gelijk aan 90º
Bij c: Maak een goede schets van driehoek AFC en verwerk de gegevens uit opgave a. en b.
In driehoek BCF geldt:
CF2 = BC2 + BF2
CF2 = 62 + 42
CF2 = 52
CF = √52
tan(∠CEF) = O/A = CF/EF = √52 / 6
∠CEF = tan-1( √52 / 6 )
∠CEF ≈ 50,24º
b.
Via Pythagoras zien we dat AF = FC = √52.
Dus driehoek ACF is gelijkbenig.
c.
In driehoek ABC geldt: AC = √72 (Pythagoras)
cos(∠MCF) = A/S = CM/CF
cos(∠MCF) = ½√72 / √52
∠MCF = cos-1( ½√72 / √52 )
∠MCF ≈ 53,96º
Dus ∠ACF = ∠MCF = 54º

48.
a. ∠DME ≈ 45,2º
b. ∠CMF ≈ 42,7º
c. ∠MPN ≈ 48,7º
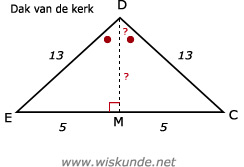
49.
DE2 = EM2 + DM2
132 = 52 + DM2
DM2 = 144
DM = √144
DM = 12
Dus de hoogte van de toren is: AE + DM = 40 + 12 = 52 meter.
b.
sin(∠CDM) = O/S = CM/CD = 5/13
∠CDM = sin-1(5/13)
∠CDM ≈ 22,62º
Dus ∠CDE = 2 x ∠CDM = 2 x 22,62º = 45,24º.
c.
In driehoek FMI geldt: FI = √2729 (Pythagoras).
In driehoek FID geldt: tan(∠IFD) = DI / FI = 15 / √2729
∠IFD = tan-1( 15/√2729 )
∠IFD ≈ 16,0º
Tip:
Bij a: hoogte toren = AE + DM
Bij b: ∠CDE is 2x ∠CDM. Bereken eerst ∠CDM met de sinus.
a.Bij a: hoogte toren = AE + DM
Bij b: ∠CDE is 2x ∠CDM. Bereken eerst ∠CDM met de sinus.
DE2 = EM2 + DM2
132 = 52 + DM2
DM2 = 144
DM = √144
DM = 12
Dus de hoogte van de toren is: AE + DM = 40 + 12 = 52 meter.
b.
sin(∠CDM) = O/S = CM/CD = 5/13
∠CDM = sin-1(5/13)
∠CDM ≈ 22,62º
Dus ∠CDE = 2 x ∠CDM = 2 x 22,62º = 45,24º.
c.
In driehoek FMI geldt: FI = √2729 (Pythagoras).
In driehoek FID geldt: tan(∠IFD) = DI / FI = 15 / √2729
∠IFD = tan-1( 15/√2729 )
∠IFD ≈ 16,0º

Andere paragrafen:
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


