TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.3 Berekeningen met sinus, cosinus & tangens VWO 3
Boek: Getal & Ruimte - Goniometrie VWO 3 (deel 2) opgaven 28 t/m 38, 2011Werkschema: hoeken en zijden berekenen:
- Lees de opdracht goed en overzie het probleem
- Maak een schets van de juiste rechthoekige driehoek
- Teken een hulplijn, bijvoorbeeld een loodlijn
- Kies de juiste goniometrische verhouding (sin, cos of tan) op basis van je schets
- Lees de opdracht goed en overzie het probleem
- Maak een schets van de juiste rechthoekige driehoek
- Teken een hulplijn, bijvoorbeeld een loodlijn
- Kies de juiste goniometrische verhouding (sin, cos of tan) op basis van je schets
28.
cos(∠C) = aanliggende rechthoekszijde / schuine zijde = A/S = BC/AC
cos(68º) = BC/3
BC = cos(68º) * 3
BC ≈ 1,1
b.
Hij zit 3,5 - 1,1 = 2,4 meter boven de grond.
29.
∠A = tan-1(0,15) ≈ 8,53º
sin(∠A) = BC / AC
AC = ( 1 x 550 ) / sin(8,53º) ≈ 3708 meter
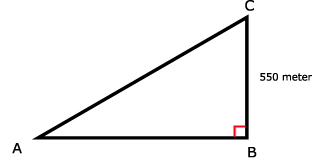
30.
6 minuten = 360 seconden
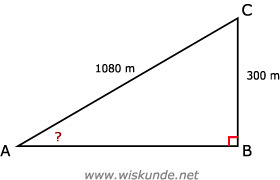
3 m/s => 360 x 3 = 1080 meter
Dus AC = 1080 meter.
b.
hellings% = tan(∠A) x 100%
AB2 + BC2 = AC2
AB2 + 3002 = 10802
AB2 = 1076400
AB = √1076400
AB ≈ 1037,5
tan(∠A) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = BC/AB = 300/1037,5
hellings % = (300 / 1037,5) x 100% = 28,9%
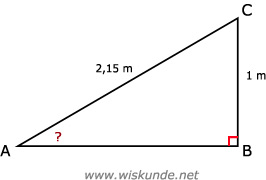
31.
∠A = sin-1( 1 / 2,15)
∠A ≈ 27,7º
Dus de hellingshoek van de stuwdamwand is ≈ 27,7º.
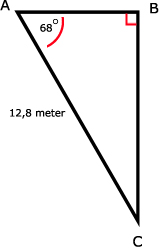
32.
sin(68º) = BC/12,8
Dus BC = 12,8 x sin(68º) ≈ 11,87
Dus diepte van het water is ongeveer 12 meter.
33.
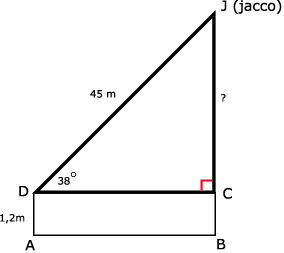
sin(∠D) = overstaande rechthoekszijde / schuine zijde = O/S = JC / DJ
sin(38º) = JC/45
JC = 45 x sin(38º)
JC ≈ 27,7 meter
Jacco hangt dus op hoogte: 27,7 + 1,2 = 28,9 meter.
b.
sin(∠D) = overstaande rechthoekszijde / schuine zijde = O/S = JC / DJ
JC wordt nu: 27,7 + 9 = 36,7
sin(∠D) = JC / DJ = 36,7/45
∠D = sin-1(36,7/45)
∠D ≈ 54,6º
Kabel maakt een hoek van: ∠D ≈ 54,6º
34.
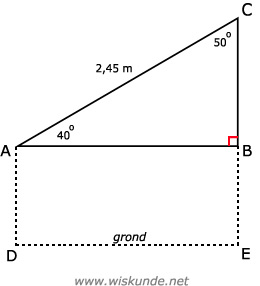
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = BC/AC
sin(40º) = BC/2,45
BC = sin(40º) * 2,45
BC ≈ 1,57
Dus hoogte van de schommel AD = 3,05 - BC = 3,05 - 1,57 = 1,48 meter.
Dat is dus 148 cm.
b.
cos(∠C) = aanliggende rechthoekszijde / schuine zijde = A/S = BC/AC
cos(∠C) = 1 / 2,45
∠C = cos-1(1 / 2,45)
∠C ≈ 65,9º
Dus de wijkhoek is ≈ 65,9º.
35.
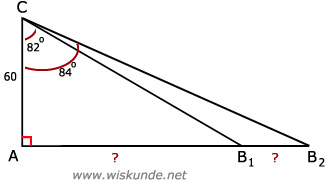
tan(∠C) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = AB1/AC
tan(82º) = AB1/60
AB1 = tan(82º) * 60
AB1 ≈ 426,9
Dus de afstand tussen boei 1 en de vuurtoren is 426,9 meter.
b.
tan(∠C) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = AB2/AC
tan(84º) = AB2/60
AB2 = tan(84º) * 60
AB2 ≈ 570,9
Dus de afstand tussen de twee boeien is: AB2 - AB1 = 570,9 - 426,9 = 144 meter
36.
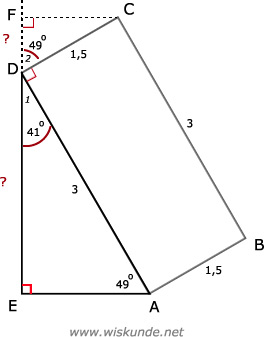
∠D2 = 180º - 90º - 41º = 49º
a.
Bereken DE =>
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = DE/AD
sin(49º) = DE/3
DE = sin(49º) * 3
DE ≈ 2,26
Dus de kist raakt de muur op een hoogte van 2,26 meter.
b.
Bereken DF =>
cos(∠D2) = aanliggende rechthoekszijde / schuine zijde = A/S = DF/CD
cos(49º) = DF/1,5
DF = cos(49º) * 1,5
DF ≈ 0,98
Dus EF = DE + DF = 2,26 + 0,98 = 3,24
Dus de hoogte van punt C is 3,24 meter.
c.
Als de kist terugvalt, zit A ongeveer 1,34 meter van de muur.
37.
Bereken eerst ∠B3: 180º - 90º - 40º = 50º
sin(∠B3) = overstaande rechthoekszijde / schuine zijde = O/S = CE/BC
sin(50º) = CE/40
CE = sin(50º) * 40
CE ≈ 30,64
b.
∠C3 = 180º - ∠E - ∠B3 = 180º - 90º - 50º = 40º
∠C2 = 90º - ∠C3 = 90º - 40º = 50º
∠C1 = 90º - ∠C2 = 90º - 50º = 40º
tan(∠C1) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = DF/CD
tan(40º) = DF/30
DF = tan(40º) * 30
DF ≈ 25,17
Oppervlakte driehoek CDF = 1/2 x basis x hoogte
Opp(CDF) = 1/2 x CD x DF
Opp(CDF) = 1/2 x 30 x 25,17
Opp(CDF) = 377,55 cm2
Dus inhoud van weggelopen hoeveelheid water:
Opp(CDF) x hoogte = 377,55 cm2 x 30 cm = 11 326,5 cm3
Inhoud van de totale bak = l x b x h = 30 x 30 x 40 = 36 000 cm3
Inhoud weggelopen hoeveelheid water = 11 326,5 cm3
Je houdt over aan water wat in de bak achter blijft: 24 673,5 cm3
Je weet dat 1 liter = 1000 cm3
Dus er zit na de kanteling nog 24,6 liter water in de bak.
Tip:
Hoekpunt A in de rechthoekige driehoek komt overeen met de plek waar Matthijs zit.
De getoonde driehoek hoort dus bij de situatie van de schommel.
a.Hoekpunt A in de rechthoekige driehoek komt overeen met de plek waar Matthijs zit.
De getoonde driehoek hoort dus bij de situatie van de schommel.
cos(∠C) = aanliggende rechthoekszijde / schuine zijde = A/S = BC/AC
cos(68º) = BC/3
BC = cos(68º) * 3
BC ≈ 1,1
b.
Hij zit 3,5 - 1,1 = 2,4 meter boven de grond.
29.
Tip:
BC in de driehoek is 1284 meter - 734 meter = 550 meter.
De tan(∠A) = 0,15, want hellingspercentage is 15%. BC in de driehoek is 1284 meter - 734 meter = 550 meter.
∠A = tan-1(0,15) ≈ 8,53º
sin(∠A) = BC / AC
AC = ( 1 x 550 ) / sin(8,53º) ≈ 3708 meter

30.
Tip:
Maak eerst een goede schets van de situatie.
Bereken dan de lengte van AC (zie opgave a.).
Bereken AB met de Stelling van Pythagoras.
Bereken dan tan(∠A)
a.Maak eerst een goede schets van de situatie.
Bereken dan de lengte van AC (zie opgave a.).
Bereken AB met de Stelling van Pythagoras.
Bereken dan tan(∠A)
6 minuten = 360 seconden
3 m/s => 360 x 3 = 1080 meter
Dus AC = 1080 meter.
b.
hellings% = tan(∠A) x 100%
AB2 + BC2 = AC2
AB2 + 3002 = 10802
AB2 = 1076400
AB = √1076400
AB ≈ 1037,5
tan(∠A) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = BC/AB = 300/1037,5
hellings % = (300 / 1037,5) x 100% = 28,9%

31.
Tip:
Maak een schets. Bedenk: 249 - 248 = 1 meter hoogteverschil (verticaal)
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = BC/AC = 1 / 2,15Maak een schets. Bedenk: 249 - 248 = 1 meter hoogteverschil (verticaal)
∠A = sin-1( 1 / 2,15)
∠A ≈ 27,7º
Dus de hellingshoek van de stuwdamwand is ≈ 27,7º.

32.
Tip:
Bekijk de schets. BC is de diepte van het water.
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = BC / AC Bekijk de schets. BC is de diepte van het water.
sin(68º) = BC/12,8
Dus BC = 12,8 x sin(68º) ≈ 11,87
Dus diepte van het water is ongeveer 12 meter.

33.
Tip:
Bij a: Hoogte Jacco is JC + hoogte van de boot.
Bij b: Hoogte JC wordt 9 meter hoger en de lijn DJ blijft 45 meter.
a.Bij a: Hoogte Jacco is JC + hoogte van de boot.
Bij b: Hoogte JC wordt 9 meter hoger en de lijn DJ blijft 45 meter.
sin(∠D) = overstaande rechthoekszijde / schuine zijde = O/S = JC / DJ
sin(38º) = JC/45
JC = 45 x sin(38º)
JC ≈ 27,7 meter
Jacco hangt dus op hoogte: 27,7 + 1,2 = 28,9 meter.
b.
sin(∠D) = overstaande rechthoekszijde / schuine zijde = O/S = JC / DJ
JC wordt nu: 27,7 + 9 = 36,7
sin(∠D) = JC / DJ = 36,7/45
∠D = sin-1(36,7/45)
∠D ≈ 54,6º
Kabel maakt een hoek van: ∠D ≈ 54,6º

34.
Tip:
Bij a: Bereken eerst BC. Dan de hoogte van de schommel AD = 3,05 - BC.
∠A = 180º - 90º - 50º = 40º
Bij b: De hoogte BC wordt dan 3,05 - 2,05 = 1 (meter)
a.Bij a: Bereken eerst BC. Dan de hoogte van de schommel AD = 3,05 - BC.
∠A = 180º - 90º - 50º = 40º
Bij b: De hoogte BC wordt dan 3,05 - 2,05 = 1 (meter)
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = BC/AC
sin(40º) = BC/2,45
BC = sin(40º) * 2,45
BC ≈ 1,57
Dus hoogte van de schommel AD = 3,05 - BC = 3,05 - 1,57 = 1,48 meter.
Dat is dus 148 cm.
b.
cos(∠C) = aanliggende rechthoekszijde / schuine zijde = A/S = BC/AC
cos(∠C) = 1 / 2,45
∠C = cos-1(1 / 2,45)
∠C ≈ 65,9º
Dus de wijkhoek is ≈ 65,9º.

35.
Tip:
Bij a: bereken de afstand tussen A en B1
Bij b: bereken de afstand tussen B1 en B2 (Boei1 en Boei2)
a.Bij a: bereken de afstand tussen A en B1
Bij b: bereken de afstand tussen B1 en B2 (Boei1 en Boei2)
tan(∠C) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = AB1/AC
tan(82º) = AB1/60
AB1 = tan(82º) * 60
AB1 ≈ 426,9
Dus de afstand tussen boei 1 en de vuurtoren is 426,9 meter.
b.
tan(∠C) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = AB2/AC
tan(84º) = AB2/60
AB2 = tan(84º) * 60
AB2 ≈ 570,9
Dus de afstand tussen de twee boeien is: AB2 - AB1 = 570,9 - 426,9 = 144 meter

36.
Tip:
Bij a: Bereken de hoogte DE.
Bij b: Bereken DF en tel daarbij op DE. Je krijgt dan EF. En EF is gelijk aan de hoogte van punt C.
∠D1 = 180º - 90º - 49º = 41ºBij a: Bereken de hoogte DE.
Bij b: Bereken DF en tel daarbij op DE. Je krijgt dan EF. En EF is gelijk aan de hoogte van punt C.
∠D2 = 180º - 90º - 41º = 49º
a.
Bereken DE =>
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = DE/AD
sin(49º) = DE/3
DE = sin(49º) * 3
DE ≈ 2,26
Dus de kist raakt de muur op een hoogte van 2,26 meter.
b.
Bereken DF =>
cos(∠D2) = aanliggende rechthoekszijde / schuine zijde = A/S = DF/CD
cos(49º) = DF/1,5
DF = cos(49º) * 1,5
DF ≈ 0,98
Dus EF = DE + DF = 2,26 + 0,98 = 3,24
Dus de hoogte van punt C is 3,24 meter.
c.
Als de kist terugvalt, zit A ongeveer 1,34 meter van de muur.

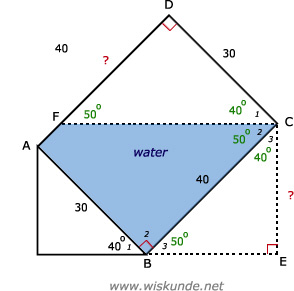
37.
Tip:
Bij a: bereken CE
Bij b: Inhoud van het weggelopen water vormt een prisma met grondvlak CDF. Bereken de oppervlakte van driehoek CDF.
Trek dan van de totale inhoud van de bak (lxbxh) de inhoud van het weggelopen hoeveelheid water af. Je houdt dan de inhoud van het water over (blauw).
a.Bij a: bereken CE
Bij b: Inhoud van het weggelopen water vormt een prisma met grondvlak CDF. Bereken de oppervlakte van driehoek CDF.
Trek dan van de totale inhoud van de bak (lxbxh) de inhoud van het weggelopen hoeveelheid water af. Je houdt dan de inhoud van het water over (blauw).
Bereken eerst ∠B3: 180º - 90º - 40º = 50º
sin(∠B3) = overstaande rechthoekszijde / schuine zijde = O/S = CE/BC
sin(50º) = CE/40
CE = sin(50º) * 40
CE ≈ 30,64
b.
∠C3 = 180º - ∠E - ∠B3 = 180º - 90º - 50º = 40º
∠C2 = 90º - ∠C3 = 90º - 40º = 50º
∠C1 = 90º - ∠C2 = 90º - 50º = 40º
tan(∠C1) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = DF/CD
tan(40º) = DF/30
DF = tan(40º) * 30
DF ≈ 25,17
Oppervlakte driehoek CDF = 1/2 x basis x hoogte
Opp(CDF) = 1/2 x CD x DF
Opp(CDF) = 1/2 x 30 x 25,17
Opp(CDF) = 377,55 cm2
Dus inhoud van weggelopen hoeveelheid water:
Opp(CDF) x hoogte = 377,55 cm2 x 30 cm = 11 326,5 cm3
Inhoud van de totale bak = l x b x h = 30 x 30 x 40 = 36 000 cm3
Inhoud weggelopen hoeveelheid water = 11 326,5 cm3
Je houdt over aan water wat in de bak achter blijft: 24 673,5 cm3
Je weet dat 1 liter = 1000 cm3
Dus er zit na de kanteling nog 24,6 liter water in de bak.

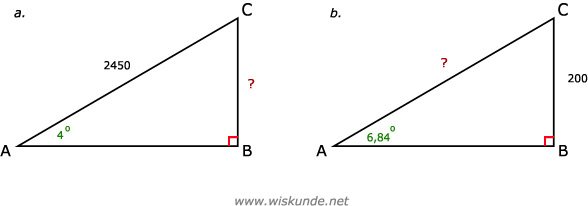
38.
Een kwartier lopen dan heeft hij afgelegd: 9,8 / 4 = 2,45 km. Dat is 2450 meter.
Bereken eerst hoek A in graden.
tan(∠A) = 0,07
∠A = tan-1(0,07)
∠A ≈ 4,00º
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = BC/AC
sin(4º) = BC/2450
BC = sin(4º) * 2450
BC ≈ 170,9
Dus het hoogteverschil is ongeveer 171 meter.
b. Zie de afbeelding:
tan(∠A) = 0,12
∠A = tan-1(0,12)
∠A ≈ 6,84º
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = BC/AC
sin(6,84º) = 200/AC
AC = 200 / sin(6,84º)
AC ≈ 1679,3 (meter)
Dus AC is ongeveer 1,6793 km.
Dan 1,6793 / 6 ≈ 0,28 uur
0,28 uur x 60 minuten is 16,8 minuten.
Dus hij moet 16,8 minuten lopen met een snelheid van 6 km/uur om een hoogteverschil van 200 meter te krijgen.
Tip:
Bij a: Bereken de hoogte BC
Bij b: Bereken de afstand AC
Als hellingspercentage gelijk is aan 7% dan: tan(∠A) = 0,07.
Met de tan-1 bereken je dan de hoek in graden.
a. Zie de afbeelding:Bij a: Bereken de hoogte BC
Bij b: Bereken de afstand AC
Als hellingspercentage gelijk is aan 7% dan: tan(∠A) = 0,07.
Met de tan-1 bereken je dan de hoek in graden.
Een kwartier lopen dan heeft hij afgelegd: 9,8 / 4 = 2,45 km. Dat is 2450 meter.
Bereken eerst hoek A in graden.
tan(∠A) = 0,07
∠A = tan-1(0,07)
∠A ≈ 4,00º
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = BC/AC
sin(4º) = BC/2450
BC = sin(4º) * 2450
BC ≈ 170,9
Dus het hoogteverschil is ongeveer 171 meter.
b. Zie de afbeelding:
tan(∠A) = 0,12
∠A = tan-1(0,12)
∠A ≈ 6,84º
sin(∠A) = overstaande rechthoekszijde / schuine zijde = O/S = BC/AC
sin(6,84º) = 200/AC
AC = 200 / sin(6,84º)
AC ≈ 1679,3 (meter)
Dus AC is ongeveer 1,6793 km.
Dan 1,6793 / 6 ≈ 0,28 uur
0,28 uur x 60 minuten is 16,8 minuten.
Dus hij moet 16,8 minuten lopen met een snelheid van 6 km/uur om een hoogteverschil van 200 meter te krijgen.

Andere paragrafen:
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


