TIP: Wil je ook toegang tot meer dan 16.900 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.1 Hellingen VWO 3
Boek: Getal & Ruimte - Goniometrie VWO 3 (deel 2) opgaven 1 t/m 9, 2011De sinus van een hoek
In de goniometrie kunnen we hoeken en zijden berekenen in een rechthoekige driehoek.
Als 2 zijden bekend zijn, dan kunnen we met de Stelling van Pythagoras, de 3e zijde berekenen.
Zijn 2 hoeken bekend, dan kunnen we met de hoekensom (som is gelijk aan 180º) de 3e hoek berekenen.
Maar wat nu als er maar 1 hoek en 1 zijde bekend is? Dan maken we gebruik van de goniometrische verhoudingen.
De sinus van een hellingshoek is gelijk aan: verticale verplaatsing / schuine zijde (Denk aan: SOS CAS TOA)
In de goniometrie kunnen we hoeken en zijden berekenen in een rechthoekige driehoek.
Als 2 zijden bekend zijn, dan kunnen we met de Stelling van Pythagoras, de 3e zijde berekenen.
Zijn 2 hoeken bekend, dan kunnen we met de hoekensom (som is gelijk aan 180º) de 3e hoek berekenen.
Maar wat nu als er maar 1 hoek en 1 zijde bekend is? Dan maken we gebruik van de goniometrische verhoudingen.
De sinus van een hellingshoek is gelijk aan: verticale verplaatsing / schuine zijde (Denk aan: SOS CAS TOA)
1.
helling 2: 0,5
helling 3: 0,5
b. Je kunt de drie hellingen in een snavelfiguur tekenen omdat ze allemaal een hoek van 30 graden hebben.
2.
a. Lengte parcours is ongeveer 5,0 cm. De verhouding wordt dan: 3 / 5,0 = 0,6.
b. Lengte parcours is ongeveer 6,6 cm. De verhouding wordt dan: 4 / 6,6 ≈ 0,6.
3.
b. 27,20
c. 0,29
d. 0,49
e. 0,69
f. 7,08
4.
∠ B ≈ 10,9º
∠ C ≈ 52,0º
5.
∠A = sin-1(2/5)
∠A ≈ 23,58º
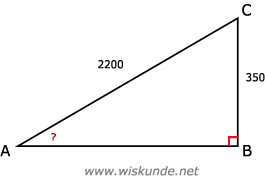
6.
∠A = sin-1(350/2200)
∠A ≈ 9,2º
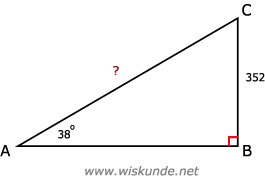
7.
sin(38º) = 352/AC
AC = 352 / sin(38º)
AC ≈ 571,74 (meter)
Dus lengte parcours ≈ 572 meter.
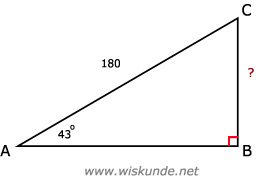
8.
sin(43º) = BC/180
BC = sin(43º) * 180
BC ≈ 122,76 (meter)
Hoogte vlieger = 122,76 + 1 ≈ 124 meter.
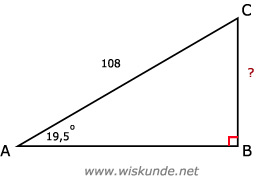
9.
sin(∠A) = verticale verplaatsing / schuine zijde = BC/AC
sin(19,5º) = BC/108
BC = sin(19,5º) * 108
BC ≈ 36,05 (meter)
Dus het hoogteverschil is ongeveer 36,05 meter.
b.
Klim per trede = 36,05 m / 250 = 3605 cm / 250 = 14,42 cm.
c.
Aantal keer op en neer per uur: 20
Tip:
De driehoeken zijn gelijkvormig.
a. helling 1: 0,5De driehoeken zijn gelijkvormig.
helling 2: 0,5
helling 3: 0,5
b. Je kunt de drie hellingen in een snavelfiguur tekenen omdat ze allemaal een hoek van 30 graden hebben.
2.
a. Lengte parcours is ongeveer 5,0 cm. De verhouding wordt dan: 3 / 5,0 = 0,6.
b. Lengte parcours is ongeveer 6,6 cm. De verhouding wordt dan: 4 / 6,6 ≈ 0,6.
3.
Tip:
Let op: op je rekenmachine heb je een (SIN)-knop en een (SIN-1)-knop.
a. 24,05Let op: op je rekenmachine heb je een (SIN)-knop en een (SIN-1)-knop.
b. 27,20
c. 0,29
d. 0,49
e. 0,69
f. 7,08
4.
Tip:
Wil je de hoek in graden weten? Gebruik dan de (SIN-1)-knop.
∠ A ≈ 33,5º Wil je de hoek in graden weten? Gebruik dan de (SIN-1)-knop.
∠ B ≈ 10,9º
∠ C ≈ 52,0º
5.
Tip:
Maak eventueel een schets van een driehoek en vul in wat je weet.
sin(∠A) = verticale verplaatsing / schuine zijde = 2/5Maak eventueel een schets van een driehoek en vul in wat je weet.
∠A = sin-1(2/5)
∠A ≈ 23,58º
6.
Tip:
Maak een schets van de situatie. Gevraagd de hoek in graden.
sin(∠A) = verticale verplaatsing / schuine zijde = BC/AC = 350/2200Maak een schets van de situatie. Gevraagd de hoek in graden.
∠A = sin-1(350/2200)
∠A ≈ 9,2º

7.
Tip:
Maak een schets en vul in wat je weet. Nu is de hoek in graden wel bekend. Gevraagd de schuine zijde.
sin(∠A) = verticale verplaatsing / schuine zijde = BC/ACMaak een schets en vul in wat je weet. Nu is de hoek in graden wel bekend. Gevraagd de schuine zijde.
sin(38º) = 352/AC
AC = 352 / sin(38º)
AC ≈ 571,74 (meter)
Dus lengte parcours ≈ 572 meter.

8.
Tip:
Hoogte vlieger is BC + 1 meter
sin(∠A) = verticale verplaatsing / schuine zijde = BC/ACHoogte vlieger is BC + 1 meter
sin(43º) = BC/180
BC = sin(43º) * 180
BC ≈ 122,76 (meter)
Hoogte vlieger = 122,76 + 1 ≈ 124 meter.

9.
Tip:
Maak een schets. Je zou BC ook kunnen zien als de hoogte van de trap.
a.Maak een schets. Je zou BC ook kunnen zien als de hoogte van de trap.
sin(∠A) = verticale verplaatsing / schuine zijde = BC/AC
sin(19,5º) = BC/108
BC = sin(19,5º) * 108
BC ≈ 36,05 (meter)
Dus het hoogteverschil is ongeveer 36,05 meter.
b.
Klim per trede = 36,05 m / 250 = 3605 cm / 250 = 14,42 cm.
c.
Aantal keer op en neer per uur: 20

Andere paragrafen:
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


